指向学科实践的小学数学实验场景建构

摘 要：指向学科实践的小学数学实验场景，呈现出多元样态：可以是保障数学实验有效开展的场域，也可以是支持儿童用实验方式建构数学知识的情境，还可以是促进儿童自主、合作、探究开展实验的活动。具体建构中，要突出“做”“思”结合，遵循“三强调、三保障”原则：强调积极行动，保障亲历实践；强调真实情境，保障完整过程；强调多维交互，保障意义创生。

关键词：小学数学；学科实践；数学实验；实验场景

《义务教育课程方案（2022年版）》（以下简称“新课程方案”）提出“强化学科实践”，“注重‘做中学’，引导学生参与学科探究活动，经历发现问题、解决问题、建构知识、运用知识的过程，体会学科思想方法”。^［1］这表明，“学科实践”已经成为一种重要的教学规程和学习方式。在小学数学教学中，作为学科实践一种重要方式的数学实验，强调通过具身体验与探索，对数与形的表征素材进行数学化操作，来建构数学概念、验证数学结论、探索数学规律、解决数学问题^［2］，驱动学生像数学家一样去思考与实践。其中，数学实验场景的建构至关重要。

一、基本原则

实验场景是数学实验赖以发生的背景、基础和条件，是物理空间、关系空间和意义空间的有机交融。在学科实践视域下，小学数学实验场景突出“做”“思”结合，需要遵循以下原则：

（一）强调积极行动，保障亲历实践

数学学习需要思考，更需要行动。对于小学生来说，动起来的学习更能调动其积极性。数学实验场景的建构和设置，就是要发挥“做中学”的优势，给学生创设一个适合操作且利于体验的环境，将枯燥的说教转变为沉浸式经历，将抽象的数学问题转化为有趣的数学活动，让每个学生都有条件成为真正的行动主体，集结人的知、情、意、行心理活动诸领域，共同参与实践活动。

（二）强调真实情境，保障完整过程

建构主义认为，情境是学习环境的四大核心要素之一，由情感氛围、物理空间和人物关系构成。指向学科实践的数学实验场景，应以真实情境为内核：一方面，关注生活现实、数学现实以及其他相关学科现实，尽可能地建立数学知识与已有经验的联结，营造身临其境的现实感，激发学生持续的探究欲望和解决问题的迫切感；另一方面，通过“做”“思”结合的真实情境，将实践活动拉长，以保障学生从实验开始便深度介入，主动提出真实问题、设计解决方案、开展探究活动，完整地经历学习过程。在这种“慢推进”中，学生能够真正体会数学的美妙与价值，收获精神的丰盈与人格的发展。这是数学实验的育人价值所在。

（三）强调多维交互，保障意义创生

教学在本质上是以知识为中介的人际交往和互动。如何实现真正的交互？数学实验教学给出了回应：一是组建以学生为中心，缔结教师、同伴、工具、互联网等多维链接的交互网络，形成学习共同体；二是创建生生之间合作、协商、讨论、争辩、分享等多维融合的交互样态，鼓励学生共同参与实践活动。其间，学生也可以作为实验场景建构主体，不断与新世界、新领域链接，打破旧有思维模式，以新视角、新方式去思考，得出富有新意的结论。这样的过程，也是数学意义创生的过程。由此，学生的知识与技能不断发展，核心素养也就能不断提升。

二、具体样态

“在小学教学中，运用各种生活的、教学的场景启动儿童思维，点燃儿童思维，用以反映场景，建构认知体系。运用场景学习，既可以把场景事物作为认识对象，也可以把场景作为推动儿童思维发展的诱因。”^［3］指向学科实践的数学实验场景呈现出多元样态：可以是保障数学实验有效开展的场域，也可以是支持儿童用实验方式建构数学知识的情境，还可以是促进儿童自主、合作、探究开展实验的活动。

（一）场域场景

我们应打破时空束缚，创建全场域数学实验空间，将数学实验从课堂延伸到课后，从校园拓展到校外（包括家庭）。这个全场域，主要包括以下三个方面：

1.学校“数学实验室”

依托具身认知理论建设“数学实验室”，是学校为学生实践、探索数学而设置的专用场景。数学实验室具有如下优势：以浓郁的数学文化氛围，激活学生数学实验的需求；以便于合作的座位布置、与数学内容相匹配的结构化实验工具，为学生高质量开展数学实验提供物化条件；以信息技术的深度融合和网络画板、AR等数字技术赋能的实验环境，为学生带来更多个性化的数学学习体验。比如，提供精准的天平、台秤用于“认识千克和克”，让学生在准确操作中反复体验质量单位；学习“平行和垂直”后，动手刻画物体特定的位置关系……数学实验室能提供专业化工具和技术支持，给学生开展数学实验提供便利。

2.班级“数学实验角”

具身认知是在身体作用于现实世界的数学活动中发生的，伴随主体的个性化需求，形成即时性和持续性心理效应。“数学实验角”往往设置在班级教室角落，一般可由“实验箱”“实验台”或“实验墙”构成空间存在，为学生提供随时动手开展数学实验的活动平台。班级“数学实验角”备有的工具与教材配套，具有易获取、可利用、高原创的特点，而且引导和鼓励师生自制米尺、量绳、步弓、圆规与三角板等数学实验工具。因此，学生课堂上没弄明白的知识点，课间可随时通过“数学实验角”开展自主实验，从而进一步认识和理解课堂所学。比如，四年级学习《三角形的稳定性》，学生课间在“实验台”自发用活动小棒制作三角形和四边形框架，在实践中对比两种图形的特性，发展空间观念。五年级学习《认识公顷》，学生课后利用班级“实验箱”中的工具，自行组织测量学校操场面积。如此，将“做”“思”结合的理念与数学知识的应用延续到课后，让动手实验逐渐成为自觉。

3.家庭“数学实验场”

将数学实验的场域延展到家庭，就有了家庭“数学实验场”：基于对课内知识不同程度的理解，在家长的参与和指导下，学生结合预习和作业，动手“做数学”，开展不同层次的自主探究和“再创造”。比如，学习《平行四边形、三角形和梯形的面积计算》，可这样建构家庭“数学实验场”：有的结合传统文化中“出入相补”原理进行公式“再探索”，通过折纸、裁剪、拼凑等操作，拓展三角形模型研究，把三角形面积计算公式“底乘高除以2”，变化为“底除以2（半底）乘高” 或“高除以2（半高）乘底”，借助长方形完成推导；也有的通过画图与剪纸，将三角形看作上底为0的梯形，将平行四边形看作上下底等长的梯形，从而用梯形面积公式统一三角形、平行四边形的面积计算。学生将在家庭“数学实验场”取得的成果，带到班级进行“再交流”“再思考”，实现个体与群体探究场景之间的互联互通。

（二）情境场景

教师还应创设恰当的数学情境，形成数学实验的心理氛围，为数学知识的实践与探索提供适切的支持。作为数学实验场景的情境，可以引导学生快速进入实验，主要包括生活情境、游戏情境、问题情境。

1.生活情境

数学实验中，可以通过生活情境引入实验课题。比如，《乘法分配律》一课，教师运用投影画图和语言讲述，创设班长小明和班级球队5位队员一起到服装店购置球衣的生活情境：当选定了款式，明确了上衣每件a元和裤子每条b元，结算付款时，班长小明将6件上衣总价与6条裤子总价相加，得到购衣总价（6a＋6b）元；另一位队员将上衣单价与裤子单价相加，算出每套单价（a＋b）元，乘6人得到总价（a＋b）×6元。由此，引出6a＋6b=（a＋b）×6。学生对此情境中同伴结伴购衣以及结算付款的生活情境比较熟悉，确认两种计算方式均合理，等式成立，很便捷地得到了乘法分配律等式模型。

2.游戏情境

数学实验中，可以通过游戏情境引入实验课题。比如，《用数对确定位置》一课，教师创设了“抓捕光头强”的游戏情境：让学生模拟警察角色，运用点子图、方格板等工具，精准搜捕“光头强”。其间，从森林小道（一维）到密林深处（二维）的位置变化，激发学生产生认知冲突和挑战欲望，即在图上（或地面）实现确定位置的空间突破，催生数对模型的建立。最后，创生出平面直角坐标系第一象限的雏形，形成用数对确定位置的基本思路和坐标方法。

3.问题情境

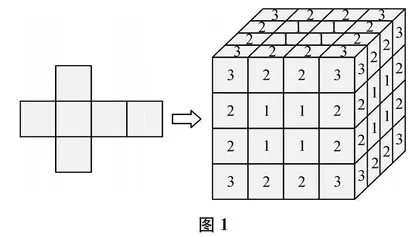
数学实验中，还可以通过问题情境引入实验课题。比如，《认识长方体和正方体》一课，教师创设这样的问题情境：“把一个棱长是4厘米的正方体表面涂上红色。现在将每条棱长平分为四段画上平行线，沿着这些平行线把正方体切开，得到若干正方体小块。试问：切开后的小方块中，一面、两面和三面红色的各有多少块，表面不涂红色的有多少块？”立足这个问题情境，学生动手“做数学”：有的自备魔方；有的用铁丝扎成正方体框架模型；有的捏制胶泥正方体；有的则用带色纸板制作出棱长4厘米的正方体，并把每个面平分为16格（如图1所示）。通过对做出的正方体的观察，学生马上明白了：三面、两面和一面涂色的块数，分别与正方体的顶点数（每个顶点1块）、棱数（每条棱2块）和面数（每个面4块）有关，分别是8（8×1）块、24（12×2）块、24（6×4）块；而不涂红色（即内二层不带色）的，则从总块数中减去表层带色的，就是8块。

（三）活动场景

教师应通过恰当的活动场景，引导学生在数学实验中，经历发现问题、提出问题、分析问题、解决问题的全过程。数学实验的活动场景，主要包括以下方面：

1.观察反思活动

数学实验中，可以引导学生借助对图形和数式的观察，展开联想、判断、推理、反思，从中获得新的感悟，有效地解决问题。比如，研究方阵数求和，教师出示活动要求：（1）任意画出大小不同的正方形，并在其中画出边长是1厘米的小方格；（2）用不同方法算出各自画出正方形内小方格的总数；（3）总结出正方形内小方格总数的计算方法。以边长是4厘米的正方形中所含边长是1厘米的小正方形格数为例。学生通过动手画正方形格子，点数计数，列式计算，将图形观察与列式计算对照，数形结合，换位观察，联想推理，得到正方形方阵数求和的三种方法。有的从左往右、从里往外看，依次折角分层运用连加计数（如图2所示），就得到从1开始连续奇数求和的连加算式：1+3+5+7。有的将正方形对角线垂直于水平方向，分别从上向下看每层数（如下页图3所示），从1开始每层数是连续自然数，先依次递增到最大加数4求和，再依次递减到1求和，两端对称，最大加数就是正方形边长厘米数，得到连加算式：1＋2＋3＋4＋3＋2＋1。还有的用边长厘米数自乘，即4×4便得到小方格的总数。这样，求正方形内方格总数就得到三种求法等式：1＋3＋5＋7=1＋2＋3＋4＋3＋2＋1=4×4。

2.动手操作活动

动手操作是数学实验的题中之义。比如，算理的理解和算法的提炼是运算教学的关键，同时也是一个难点。实践证明，具体和直观是理解算理、提炼算法的基本方法：让学生运用身边常见的学具（如计数器、小棒、小方块、彩纸等），借助分、摆、折、圈、画等动手操作活动，自觉地开展数学实验，可将抽象思维可视化，让算理逐步清晰，使算法自然生成，有效地实现算理与算法的融通。以《隔位退位减》一课为例，可通过计数器拨珠，动态演示连续两次从不够减的低位依次向其前一位“借”“1”，再连续两次依次在后一位当“10”去减。借助这样的动手操作活动场景，让算理与算法相互对应、交融，学生对算理和算法的理解便能水到渠成。

3.“三象”融合活动

所谓“三象”，是指数学学习中的“现象、表象、抽象”。小学阶段，很多数学知识的建构都需要经历这样的认知过程，尤其在图形与几何领域，大量概念、定理、性质在生活中都有丰富的原型和具体的应用。数学实验中，通过“三象”融合活动，让学生主动感知数学现象，在头脑里自觉呈现出不同概括水平的表象，再通过联结与综合，自主形成概括性的抽象概念。以《圆的认识》一课为例。课前，教师让学生到生活中接触各种“圆”的物体，如看到锅、碗、盆、杯等实物口边的圆形，体验各种圆形健身器械等，学生就会在头脑中留存印象，并不断调整、抽取，呈现圆的表象；课上，教师让学生根据表象选择不同的工具（如绳子、笔、直尺、圆规等）画圆，并思考“为什么用它能画出圆”，然后围绕问题动手实验探究，最终抽象出圆和画圆中“一中同长”的本质属性，并回归生活各领域进行多元应用。这样的“三象”融合活动层层递进，促使学生的空间观念、逻辑推理、应用意识等素养得到发展。

综上所述，实验场景的构建，为小学数学实验教学提供了有效的载体和抓手，切实保障学生在多维交互中亲历学科实践活动，发展学习力，形成积极的情感态度和价值观，推动创新意识的萌发和创造能力的生长。

参考文献：

［1］中华人民共和国教育部.义务教育课程方案（2022年版）［S］.北京：北京师范大学出版社，2022：14.

［2］郭庆松.小学数学实验的内涵、价值与实施［J］.小学数学教育， 2016 （7/8）：6-9.

［3］李传庚.场景学习：点燃儿童思维［M］.南京：江苏凤凰教育出版社，2016：290.