小学数学“问题提出”教学步骤解读

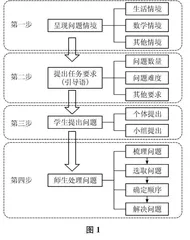
摘要：在蔡金法教授和他的合作者提出的“数学课堂中问题提出活动教学过程”的基础上，经过教学实践，修改并提出一个更精简的小学数学“问题提出”教学流程，具体包括教师呈现问题情境、教师提出任务要求、学生提出问题、师生处理问题四个步骤。其中，第一步可以呈现的问题情境包括生活情境、数学情境和其他情境，第二步一般要提出问题数量、问题难度、问题指向等方面的要求，第三步即学生根据问题情境和任务要求提出自己的问题，第四步通常包括梳理问题、选取问题、确定顺序、解决问题四个小步骤。

关键词：小学数学；问题提出；教学步骤

*感谢蔡金法教授对相关研究以及本文写作给予的重要指导。本文第一作者系“蔡金法问题提出教学工作室”成员。

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）进一步强调，要发展学生的“四能”（发现问题、提出问题、分析问题和解决问题的能力）。传统的数学教学比较重视分析问题和解决问题，而忽视发现问题和提出问题。这样不仅在学习（探究）的流程上不够完整、自然，而且不能很好地激发学生的主动性，培养学生的创新意识。［1］因此，我们更要重视发现问题和提出问题的教学。其实，“问题提出”（即广义的提出问题，包括发现问题）教学，是一种走在世界前列的教学理念。其要求教师引导学生基于某个问题情境，通过接受已知或改变已知的方式提出新的数学问题，进而对这些问题作出恰当的处理。

一种教学理念或方法要推广应用，应形成相对固定而不失灵活性的实践操作流程。蔡金法教授和他的合作者在理论研究的基础上，依据有关的实证研究和实践案例，提出了“数学课堂中问题提出活动教学过程”，给出了流程图，但未详细解释其中的各个步骤。［2］过去几年中，我们在蔡金法教授的指导下，系统学习了“问题提出”教学的理论基础和实践方法，进而根据上述教学过程进行了系统的实践。针对实践中遇到的问题，我们修改并提出了一个更精简的小学数学“问题提出”教学流程。本文对其各个步骤做具体的解读，以期为一线教师更好地落实“问题提出”教学提供操作层面的指导。

一、教学流程概述

一般地，数学课堂中的“问题提出”教学活动包括以下几个步骤：（1）教师呈现问题情境；（2）教师提出任务要求（即引导语）；（3）学生提出问题；（4）师生处理问题。其中，每一个步骤都包括一些小步骤，具体如图1所示。

这里，需要对第四步“师生处理问题”做一个说明。我们将其分为四个小步骤：“梳理问题”“选取问题”“确定顺序”和“解决问题”。其中，前三个小步骤是第四个小步骤的前期准备。当然，在实际教学中，不一定非得经过前三个小步骤，而是可以在“学生提出问题”后直接“师生解决问题”。之所以可能有前三个小步骤，是因为在实际教学中，学生可能提出五花八门的问题（有的困难，有的容易；有的是数学问题，有的不是数学问题；有的与教学目标有关，有的与教学目标无关），梳理、选取问题和确定顺序常常成为必要的步骤。

二、教学步骤解读

（一）呈现问题情境

在确定了一节课具体的教学目标和教学内容后，教师要深入浅出地解读教材，找准学生学习的起点，根据学生的年龄特征和生活经验，创设问题提出的情境，引导学生提出不同数量、不同难度、不同结构的数学问题，并促进他们的数学思考与数学理解。具体地，可以创设生活情境、数学情境和其他情境。

1. 创设生活情境

生活情境是指生活中所含的数学现象，可以用文字、符号、图表、图片、视频等形式表现。［3］无论是真实的生活情境，还是模拟的生活情境，都有助于学生提出真实、有效的数学问题。

例如，《合理安排时间》一课，石高文老师创设了“老师起床后要做的事”的生活情境，引导学生提出问题：“昨天早上，我起床晚了，醒来一看手表：哇！已经 7∶00 了。上班前，我需要完成以下几件事：穿衣服 4 分钟，整理被子 2 分钟，刷牙洗脸 6 分钟，蒸馒头 10 分钟，吃早餐 6分钟，听广播 10 分钟，骑自行车到学校 10 分钟。根据老师上班前要做的事，你能提出什么问题？”

这里，石老师创设的“老师起床后要做的事”的情境和学生的生活经验密切相关：老师起床后要做的几件事几乎是每个学生每天都要经历的。对这一情境直接而深刻的体验有利于他们提出有效的数学问题。

2. 创设数学情境

数学情境是指直接用数学概念、性质等创设的问题情境。［4］数学的表达式、文字、符号、图形等，都可以成为创设问题情境的素材。

例如，《平行四边形的面积》一课，何小平老师创设了“交换土地”的情境，给出了由真实土地抽象成的几何图形，引导学生提出问题：“王伯和李伯是同住在一个村子的好朋友，王伯住在村东，但他家的地在村西，且是长方形的（如图2所示）；李伯住在村西，他家的地却在村东，且是平行四边形的（如图3所示）。由于耕种和收获都不方便，他们想互相交换两块土地。你觉得公平吗？根据这件事情，你能提出哪些数学问题？请至少提出两个问题——当然，问题的数量没有上限。”

这里，何老师利用图形创设情境，让学生提出问题，暴露学生真实的想法，进而可以引出本节课的核心内容：平行四边形的面积是怎么算的？是否和长方形的面积计算有关联？这样，可以促进学生主动探索不同几何图形面积计算之间的数学关联。

再如，《三位数乘两位数》一课，何小平老师出示算式“145×12=”和“145×10+145×2=”，让学生分别提出一个能用这两个算式解决的实际问题。

这里，何老师利用算式创设情境，让学生结合生活经验提出实际问题，赋予算式现实意义。由数学算式到实际问题，是一种由抽象到具体的发散性思考，能帮助学生理解算式的含义，采用不同的方法计算145×12，从而更好地学习三位数乘两位数的算理和算法。

3. 创设其他情境

其他情境是指除了生活情境、数学情境之外的情境，如科学实验情境、运动比赛情境等。

例如，《体积和体积单位》一课，戚彩红老师播放两个视频：第一个视频的内容是，展示两只同样大小、盛着等量水的杯子，往一个杯子中加石头，随着石头越来越多，杯子中的水面慢慢上升（图4是一张截图）；第二个视频的内容是，展示两只同样大小的杯子，1号杯中放有一个塑料的长方体，2号杯中盛满沙子，将2号杯中的沙子倒入1号杯中，当1号杯被倒满时，2号杯中还剩下三分之一左右的沙子（下页图5是一张截图）。然后，问学生从这两个视频中能提出什么数学问题。

这里，有了科学实验情境的支撑，学生很容易感知物体对空间的占有，于是能提出“是不是所有的物体都占空间？”“是不是不同的物体所占的空间有多有少？”等问题，从而直击“体积”概念的本质内涵。

（二）提出任务要求

教师在呈现问题情境的同时，要提出具体的任务要求，也就是引导语。引导语一般要明确问题数量、问题难度、问题指向等方面的具体要求。由于问题提出教育价值的多样性与独特性，不同问题提出任务与引导语的设计所产生的效果亦不同。［5］具体来说，引导语的设计是否合理，与学生能否提出问题、能否提出多个问题、能否从不同的角度提出问题、能否提出难度不同的问题密切相关，对学生思维流畅性、发散性、灵活性、深刻性等的培养有重要影响。因此，教师要根据教学任务（目标）的不同、学生问题提出水平的不同来设计与之匹配的引导语。

引导语一般要明确所提问题的数量。例如：观察图6中的图形，请你提出尽可能多的数学问题。这个引导语对问题数量的要求是比较宽松的“尽可能多”，从而鼓励学生从不同的角度思考同一情境，训练学生的发散思维。再如：已知每套书有13本，王老师买了12套书，你能根据这两个信息，提出一个合适的数学问题吗？这个引导语明确了问题的数量是1，意在培养学生有意识地提出问题的习惯，并且能够根据信息辨析哪一个问题提得更合适。

引导语有时要明确所提问题的难易程度——一般分简单、稍难、复杂三个层次。例如：请你选择合适的数和运算符号，提出一个简单的和一个稍难的用百分数解决的数学问题。这个引导语不仅明确了问题的数量是2，而且明确了问题有易有难，能够引发学生不同层次的思考，更可以了解学生不同层次的学习水平和提问水平。

引导语有时还要明确所提问题的指向——是关于什么的。例如：请你根据这些信息提出有关面积的数学问题。这个引导语有明确的指向，要求提出的问题是有关面积的。再如：给出234、66、34三个数，请你提出两个用加、减法解决的数学问题，并让这三个数同时出现在你的问题里。这个引导语不仅明确了问题的数量是2，还有明确的指向，要求提出的问题是用加、减法解决的，并且要使三个数同时出现。

（三）学生提出问题

教师呈现问题情境、提出任务要求后，学生要根据要求提出问题。根据不同的教学内容和不同的任务要求，学生可以采用书面或口头等方式提出问题；同时，学生既可以个体或小组的形式提出问题，也可先个体提出问题，再通过小组交流，以小组的形式提出问题。

无论学生以哪种形式提出问题，教师都应该及时地记录、呈现学生的问题，可采用板书、板贴、投影等可视化的形式罗列有价值的问题。

（四）师生处理问题

学生提出问题不是“问题提出”教学的结束——合理处理学生提出的问题是教学中极富挑战性的关键步骤。由于学生的思维层次不同、表达能力不同，所提的问题可能五花八门。因此，教师要引导学生一起梳理所提的问题，选取核心问题，再确定解决问题的顺序，最后采用适切的活动类型和组织方式来解决问题。

1.梳理问题

由于学生学习经验有差异、对学习材料的理解程度有不同，提出的问题常常数量不一、视角不一、价值不一。由于问题提出本身具有较大的开放性，学生可以从自我的角度提出任何问题，因此提出的问题往往会出现重复、无序、散点状的情况。故而，教师首先要引导学生梳理问题。

一是问题的分类。由于学生生活经验不足、数学语言不规范等，所提的问题有时过于浅白、浮于表面。这时，教师要引导学生分析问题背后的一般观念和思维方式，聚焦数学本质，对问题进行归类，形成有研究价值的核心问题或问题串。这样的分类整理不仅可以让学生对问题之间的关系更为清晰，而且可以帮助学生深化对数学概念的理解。

例如，黄抗明老师执教《不规则物体的体积》一课的教学片段：

师同学们，前面我们学习了长方体、立方体的体积，今天我们要研究的是“不规则物体的体积”。（出示课题）对这个课题，你能提出什么数学问题？

（学生提出了以下问题：①什么是不规则物体？②不规则物体的体积怎么求？ ③不规则物体有什么特征？④计算不规则物体的体积也有公式吗？ ⑤学习不规则物体的体积有什么用？⑥生活中哪些物体是不规则的？⑦为什么要学习不规则物体的体积？）

师你能把这些数学问题分分类吗？

生①③⑥是关于“是什么”的问题，②④是关于“怎么做”的问题，⑤⑦是关于“为什么”的问题。

师我们可以先来解决哪一类问题？

生（齐）什么是不规则物体？

师为什么要先解决这一类问题？

生如果我们连不规则物体是什么都不知道，那怎么知道它的体积，怎么求它的体积呢？

生只有知道了什么是不规则物体，才能进一步确定它的体积，探究计算体积的方法。

在学生提出众多问题后，黄老师引导学生分类整理成“是什么”“怎么做”“为什么”三类，再引导学生思考先解决哪一类问题、为什么先解决这一类问题。这是引导学生关注知识内在逻辑关系的过程。这样的教学在很大程度上落实了新课标提出的要求：丰富学习经历与体验，发展学科思维与元认识，促进逻辑思维更高层面的建构。