凸显位值原理,掌握“用0占位”
作者: 朱蓉
摘 要:
“商中间或末尾有0的除法”是三位数除以一位数的一种特殊情况,也是《两、三位数除以一位数》单元的最后一部分内容。教学时,要凸显位值原理,帮助学生牢固掌握“用0占位”。由此,学生也能充分认识到基于十进位值制计数法计算多位数除法的算理本质:分解到各个数位上依次计算,所得结果(数值)放在正确的数位上。
关键词:小学数学;商中间或末尾有0的除法;位值原理;计数单位
一、教前思考:让学生知道用0占位的道理
“商中间或末尾有0的除法”是苏教版小学数学三年级上册《两、三位数除以一位数》单元教学的难点。它是三位数除以一位数的一种特殊情况:求出商的最高位后,除到哪一位不够商1,就得在这一位商0,即用0占位。对此,学生容易因为0表示“什么也没有”,特别是最高位前的0不用写,而漏写商中间或末尾的0,从而导致错误。因此,教学中,不仅要让学生知道不够商1时,应该用0占位,而且要让学生理解用0占位的道理:十进位值制计数法是通过“位”和“值”(即计数单位和计数单位的个数)来计数的,因此,表示数时,不仅要让人明白“值”是多少,而且要让人看出是哪一“位”上的“值”;如果漏写了中间或末尾的0,那么其前面的“值”就会“错位”;只有不漏写中间或末尾的0,才能使所有的数值都摆在正确的数位上。如果学生还对“最高位前的0不用写,而中间或末尾的0需要写”感到困惑,那么教师可以引导学生认识到:整数(或小数点前)有最低位(个位),没有最高位,因此,可以约定最后面(右边)的是个位,而没法约定最前面(左边)的是哪一位;如此,中间或末尾有没有0会影响前面的数值从最低位数起的次序,即改变其数位,故中间或末尾的0需要写;而最高位前有没有0不影响后面的数值从最低位数起的次序,故最高位前的0不用写。
实际上,纵观人类计数(记数)的历史,可以发现,位值制计数法用最少的数字符号有效地表示数目,是数学史上的重大发明,其关键正是数字0。中国最早创用十进位值制计数法:用算筹摆出1—9各个数字,依次放在从个位起的各个数位上;因为用算筹不好表示0,于是用空白(空位)来表示。但是,有没有空格、有几个空格有时不容易看出,这就给读数(认数)带来了一些不便和混淆——虽然纵式、横式相间的算筹排列方式在一定程度上解决了这个问题。可见,用专门的符号0占位正是位值制计数法成熟的关键一步。[1]因此,教学“商中间或末尾有0的除法”时,要凸显位值原理,帮助学生牢固掌握“用0占位”。由此,学生也能充分认识到基于十进位值制计数法计算多位数除法的算理本质:分解到各个数位上依次计算,所得结果(数值)放在正确的数位上。这样教学,也符合《义务教育数学课程标准(2022年版)》所提出的“感悟计数单位在运算中的作用,感悟运算的一致性”[2]的要求。
二、教学过程:打通多位数除法的算理本质,凸显位值原理的作用
根据苏教版小学数学教材的编排,这一内容分两个课时教学,第一课时教学“被除数中间或末尾有0,导致商中间或末尾有0”(例8、例9及其“试一试”),第二课时教学“被除数中间或末尾某一位上不是0但比除数小,导致商中间或末尾有0”(例10及其“试一试”)。下面主要呈现第一课时的教学过程。
(一)复习已学的两、三位数除以一位数,感受计数的位值原理在计算中的作用
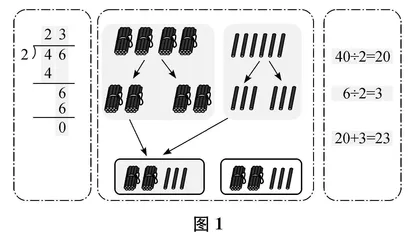
师 同学们,今天我们继续学习三位数除以一位数。还记得本单元之前学习的两、三位数除以一位数吗?它们的计算方法有什么共同的地方?(出示图1)借助这个例子想一想:先算什么?再算什么?
生 先算4除以2等于2,再算6除以2等于3,结果是23。
师 23是什么意思?它表示几个什么和几个什么?
生 表示2个十和3个一。
师 那么原来的46呢?
生 表示4个十和6个一。
师 那么这里的“4除以2等于2”和“6除以2等于3”分别是什么意思?结合分小棒的过程来说。
生 先把4个十平均分成2份,每份是2个十;再把6个一平均分成2份,每份是3个一;2个十和3个一合起来等于23。
师 所以,之前学习的两、三位数除以一位数计算方法的共同点是什么?
生 从高位开始,一位一位地除下去。
师 这么简单?有没有遇到什么特殊情况?
(学生迟疑。)
师 每一位都能除尽吗?都够除吗?
生 有时除不尽,有时不够除。
师 怎么办?
生 把除不尽的余数或不够除的数和下一位的数合在一起除。
师 非常好!两、三位数除以一位数计算方法的共同点就是:从高位开始,一位一位地除下去;遇到除不尽或不够除的情况,就把余数或本身和下一位的数合在一起除。
(稍停)那么,你有想过为什么可以这么除吗?
(学生迟疑。)
师 刚才我们说23表示什么?46表示什么?一般来说,数的组成是什么?或者说,一个数和它各位上的数有什么关系?
生 不同的数位表示不同的计数单位,其上的数字就是计数单位的个数,多位数是多个计数单位分别计数后合在一起的。
师 非常好!我们之前学过的个(一)、十、百、千等就是计数单位。我们分别对各个计数单位计数,然后把它们合起来,就得到多位数——当然,满十要进一。既然是合在一起的结果,自然可以先分开来除,再合起来。而且,分开来除,无论是某一位的数除,还是和下一位的数合在一起除,算的都是表内除法(可能有余数),可以直接利用乘法口诀试商。可见,借助数的组成或者计数的位值原理,即计数单位及其个数,能把复杂的除法变简单,即把多位数除法变成表内除法。
“商中间或末尾有0的除法”是《两、三位数除以一位数》单元的最后一部分内容。这一环节,教师引导学生复习已学的两、三位数除以一位数,发现其算法的共同点——数位分解,理解其背后的算理本质——位值原理,不仅可以教给学生一般方法,帮助学生自主探究本节课要学的商中间或末尾有0的除法,而且可以教给学生内在原理,帮助学生真正理解用0占位的关键道理——总之为新课教学做足了铺垫。这里,如果进一步看“先分开来除,再合起来”背后的道理,其实是乘法(除法)分配律,但是,因为学生没有学过,以及小学数学教学不过分强调逻辑严谨,这一结论又很符合学生的直觉,很容易被学生理解,因此教师直接讲授结论,不提运算律——而这可以看作为运算律的教学做了铺垫。
(二)学习商中间有0的除法,用位值原理高位统摄用0占位的道理
(教师出示教材例9,学生列出算式306÷3。)
师 这也是一个三位数除以一位数的式子,应该怎样算呢?
生 从高位开始,一位一位地除下去……
师 很好!请同学们试一试。
(学生在学习单上自主尝试计算。教师巡视,选择学生汇报。)
生 我是口算的:先用3个百除以3等于1个百,再用0个十除以3等于0个十,最后用6个一除以3等于2个一,所以,306÷3=102。
生 (出示图2)我用竖式计算:首先,用百位上的3除以3等于1,百位商1,再算余数,1×3=3,3-3=0,不写;其次,用十位上的0除以3等于0,十位商0,再算余数,0×3=0,0-0=0,不写;最后,用个位上的6除以3等于2,个位商2,再算余数,2×3=6,6-6=0。答案是102。
生 (出示图3)我也用竖式计算:百位上的3除以3等于1,百位商1,1×3=3,3-3=0,不写;十位上的0除以3等于0,十位商0;个位上的6除以3等于2,个位商2,2×3=6,6-6=0。答案是102。
生 (出示图4)我也用竖式计算:百位上的3除以3等于1,百位商1,1×3=3,3-3=0,不写;十位是0,跳过;个位上的6除以3等于2,个位商2,2×3=6,6-6=0。答案是12。
师 他们展示了几种方法,都对吗?
生 前三种方法是对的,第四种方法不对。
师 错在哪里?
生 十位上的0不能不写。
师 为什么?
生 十位上的0表示0个十除以3等于0个十。如果不写,结果就是12,不是102了。
师 没错。如果不写十位上的0,得数中原来在百位上的1就跑到十位上了,表示的数就变了。我们采用的计数方法叫作十进位值制计数法,不仅要知道数字是多少,而且要知道数字在哪个数位上,也就是,不仅要知道计数是多少,而且要知道计数单位是什么,才能准确表示一个数。因此,如果一个数位上没有数字(一个计数单位没有计数),那么一定要用0占位,才能保证其他数字都在正确的数位上。(稍停)这里,老师注意到一步大家没有学过但已经会了的计算:0÷3。谁能说说为什么0÷3=0。
(基于学生的回答,教师引导学生得到:0除以任何不是0的数都等于0。然后,教师引导学生利用方格图分解数位,解释算理,如图5所示。)
师 好的。回过头来看306÷3,它和之前学习的三位数除以一位数有什么不同?
生 除数中间有0,0除以任何数不是0的数都等于0。
师 没错。还有吗?
生 商中间有0,不能漏写。
师 很好!这就是我们今天学习的——(同步板书)商中间有 0的除法。学习的关键就是:注意用0占位,使得所有数字都在正确的数位上。
有了上一环节的铺垫,学生自然想到“从高位开始,一位一位地除下去”来计算新的除法,进一步感受到运算的一致性。教师放手让学生尝试,然后选择了四种不同的方法进行展示。在位值原理的引导下,多数学生的方法是正确的,但是仍然有学生犯了没有用0占位的错误。在正误的对比以及方格图的辅助下,犯错学生很快理解了用0占位的道理:被除数某一个数位上的0除以除数(不是0),商0要写在相应的数位上。这里,教师基于“0除以任何不是0的数都等于0”这一结论很容易理解的教学经验,直接跳过教材例8(教学0除以一个不是0的数),将其融入例9算法的探索过程中,从而使教学主线清晰,教学内容整体。
(三)学习商末尾有0的除法,由位值原理类比迁移用0占位的道理
教师出示教材中的“试一试”(480÷4),让学生在学习单上自主尝试计算。学生基于位值原理,继续从高位开始,一位一位地除下去;并类比迁移教材例9探索中遇到的用0占位的情况,注意到商末尾(个位)的0也不能漏写。教师点明:这就是我们今天学习的商末尾有0的除法。
从商中间有0到商末尾有0,变化不大,学生很容易类比迁移学习。在这一过程中,学生进一步感受到运算的一致性,体会位值原理,关注用0占位这一注意事项。
参考文献:
[1] 袁小明.初等数学简史[M].北京:人民教育出版社,1990:910.
[2] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022:25.