紧扣知识本质，建构分数概念

摘要：在分数知识中，“分数的意义”属于数学核心知识，主要引导学生抽象出单位“1”的概念，概括分数的意义，认识分数单位。《分数的意义》一课教学，依照分数概念的要素确立认知序列，按照认知活动的侧重精选学习素材，观照学生的认知特点确定学习方式。

关键词：《分数的意义》;知识本质;分数概念

本文系全国教育科学“十三五”规划2020年度教育部重点课题“小学数学核心知识建构的教学研究”（编号：DHA200370）的阶段性研究成果。《分数的意义》一课的教学内容是苏教版小学数学五年级下册第52页的例1及相应的练习，教学目标确定为：（1）初步理解单位“1”和分数单位的含义，从平均分和度量两个角度，经历分数意义的抽象概括过程，进一步理解分数的意义和分数单位的含义;（2）在建构分数意义的过程中，进一步培养分析、综合、抽象、概括的能力，发展数学思考;（3）在解释实际情境中分数所表示的意义等活动中，进一步体会分数的应用价值，感受分数与生活的联系，增强学习数学的兴趣。教学过程及评析如下：

一、教学过程

（一）揭示单位“1”，归纳分数的意义

1.认识单位“1”

师每到新的一年，中国邮政都会发行当年的生肖邮票。一起来看，这是今年发行的虎年邮票。（出示1枚邮票）1枚邮票可以用自然数几来表示？

生1。

（教师板书：1。）

师（出示2枚邮票）现在是几枚？也就是几个1？

生2个1。

师2个1就是——

生2。

师（出示3枚邮票）现在呢？

生3，3个1是3。

师在集邮爱好者眼里，还有一种邮票特别珍贵。一起来看，（出示4枚邮票）它是由4枚同样的邮票连在一起的四方联。这时，你觉得可以用哪个自然数表示？

生可以用4表示。

生我觉得也可以用1表示，因为4枚邮票是连在一起的，是一个整体。

（教师板书：一个整体。）

师你思考的角度与众不同，那么这时的1和以前我们所认识的1一样吗？

生不一样，现在是一个整体，原来是一个物体。

师说得真好！

（板书：一个物体。）

师既然这样，一起来看，（出示8枚邮票）把1张四方联看作“1”，那么这些邮票用几来表示呢？

生用2来表示。因为把4枚邮票看作“1”，现在有2个这样的“1”，当然就是2了。

师（出示12枚邮票）现在呢？

生应该用3来表示。

师在这里，4枚邮票所看作的“1”，其实就成了计数的单位。我们把这样的“1”又叫作单位“1”。

（补充板书：单位。）

师其实，除了可以把“4枚邮票”这样由一些物体组成的一个整体看作单位“1”，（补充板书：一些物体）我们以前研究的一个物体、一个计量单位和一些物体也都可以看作一个整体，用自然数1来表示。通常，我们把它们都叫作单位“1”。

（补充板书：一个计量单位。）

[思考：在苏教版小学数学教材中，学生是分三次认识分数的，分别安排在三年级上册、三年级下册和五年级下册。在三年级两次认识分数的教学中，学生需要理解分数既可以表示把一个物体或一个图形平均分得到的结果，也可以表示把一些物体看作一个整体平均分得到的结果。这里，以单张邮票和四方联邮票为学材，让学生理解4枚邮票所看作的“1”，实际上相当于一个计数单位，由此引出单位“1”的概念。]

2.借助单位“1”理解分数的意义

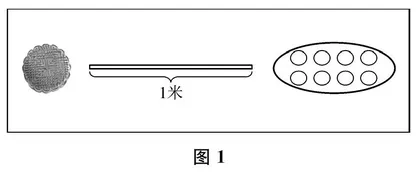
师（出示图1）一起来看大屏幕，认识吗？它们能被看作单位“1”吗？说一说这里分别把什么看作单位“1”。

生一块月饼，1米，8个圆组成的整体。

师（出示图2）把这些单位“1”平均分，会得到什么？

生分数。

（教师板书：分数。）

师那涂色部分分别是单位“1”的几分之几呢？在学习单上写一写。

（学生写。）

师谁来说说第一幅图？

生把一块月饼平均分成8份，取其中的5份，就是58。

师没错。今天我们认识了单位“1”，那么在交流这个分数时，可以说“把一块月饼看作单位‘1’，平均分成……”，谁来试试？

生把一块月饼看作单位“1”，平均分成8份，涂色部分是5份，涂色部分是这块月饼的58。

师同桌互相说一说。

（学生说。）

师剩下的两幅图呢？

生把1米看作单位“1”，平均分成8份，涂色部分是5份，涂色部分是1米的58。

生把8个圆组成的整体看作单位“1”，平均分成8份，涂色部分是5份，涂色部分是这些圆的58。

师同学们说得都非常准确！继续观察这几幅图和分数，什么相同？什么不同？

生都表示58。

生物体不同。

师物体不同，也就是单位“1”——

生（齐）不同。

师单位“1”各不相同，为什么涂色部分都可以用58表示呢？

生因为它们都是把单位“1”平均分成8份，表示这样的5份。

师是啊，不管单位“1”是什么，只要是把单位“1”平均分成8份，表示这样的5份，就可以用58表示。

[思考：本环节特意创设了三幅图的情境。这三幅图的单位“1”不同，但都是把单位“1”平均分成8份，表示这样的5份，所以都可以用分数58表示。这样的设计可以让学生在比较中进一步理解分数的产生与平均分的份数以及表示的份数密切相关。]

3.在比较中归纳分数的意义

（1）单位“1”不同，可以表示相同的分数

师刚才，同学们借助单位“1”深刻理解了58的意义。接着，（出示图3）我们来看这几幅图，看看它们分别把什么看作单位“1”，涂色部分各是单位“1”的几分之几。在学习单上写一写，写完后比一比，你有什么发现？

生第一幅图的涂色部分用14表示，这里把这些圆看作单位“1”，平均分成4份，涂色部分表示这样的1份，所以涂色的圆表示总数的14。

生第二幅图的涂色部分也用14表示，这里把这些圆看作单位“1”，平均分成4份，涂色部分表示这样的1份，所以涂色的圆表示总数的14。

生第三幅图的涂色部分还是用14表示，这里把这些圆看作单位“1”，平均分成4份，涂色部分表示这样的1份，所以涂色的圆表示总数的14。

生我发现这里都是用14表示涂色部分，但是每一幅图中涂色的圆的个数不一样。

师这是为什么呢？

生因为这里的单位“1”所包含的圆的个数不一样。单位“1”越大，它的14就越大;单位“1”越小，它的14就越小。

师从同学们的交流中不难看出，理解分数时要关注单位“1”。

（2）单位“1”相同，可以表示不同的分数

师（出示图4）这一回，单位“1”一样吗？

生一样。

师涂色三角形又是单位“1”的几分之几呢？在学习单上写一写，然后比一比，把你的发现写下来。

生第一幅图的涂色部分用56表示，这里把这些三角形看作单位“1”，平均分成6份，涂色部分表示这样的5份，所以涂色三角形表示总数的56。

生第二幅图的涂色部分用23表示，这里把这些三角形看作单位“1”，平均分成3份，涂色部分表示这样的2份，所以涂色三角形表示总数的23。

生第三幅图的涂色部分用12表示，这里把这些三角形看作单位“1”，平均分成2份，涂色部分表示这样的1份，所以涂色三角形表示总数的12。

生我发现这里的单位“1”都一样，但是平均分的份数不同，涂色的份数不同，表示的分数就不同。

师这样看来，要说清楚一个分数的意义，除了要思考单位“1”是什么，还要思考——

生（齐）单位“1”被平均分成了几份，表示了这样的几份。

（教师补充板书：平均分的份数、表示的份数。最终形成的板书如图5所示。）

师弄清了这些，也就准确理解了分数的意义。

（教师板书课题：分数的意义。）

[思考：学习分数的意义，学生需要把握三个关键：单位“1”、平均分的份数、表示的份数。基于此，本环节的第一道例题设计了单位“1”不同而平均分的份数和表示的份数都相同的情境，启发学生思考为什么表示的分数相同。第二道例题变换为单位“1”相同而表示的分数不同的情境。学生经历两种情境的对比，能进一步把握分数的意义。]

（二）引入生活情境，多元表征分数的意义

师刚才同学们动手动脑，踊跃发言，非常精彩！在生活中，我们也经常会用到分数。不过，有时单位“1”不像刚才那样“看得见”。现在，你还能理解这些分数的意义吗？

（出示：地球表面有71100被海洋覆盖。指名读一读。）

师谁来说说这里的“71100”表示的意思？

生把地球表面积看作单位“1”，平均分成100份，被海洋覆盖的面积是这样的71份。

师说得非常准确！大家闭上眼睛想一想刚才的画面。

（稍后PPT呈现地球海洋图。随后继续出示：五年级一班学生中，会打乒乓球的占34。指名读一读。）

师这里的“34”是什么意思？

生把五一班学生的人数看作单位“1”，平均分成4份，会打乒乓球的人是这样的3份。

师你能用画图的方式表示出34的含义吗？试一试。

（学生尝试画图表示，教师组织交流。）

生（展示作品，见图6）我用一个圆表示五一班学生的总数，那么涂色部分就表示会打乒乓球的人数。

生（展示作品，见图7）我用8个圆组成了一个整体，表示五一班学生的总数，那么涂色部分就表示会打乒乓球的人数。

生（展示作品，见图8）我用一条线段表示五一班学生的总数，把它平均分成4份，这样的3份就表示会打乒乓球的人数。

师从同学们的作品中，我们更加清晰形象地理解了这里的“34”的含义。虽然大家表示的单位“1”形式不同，但都表示出了会打乒乓球的人数与全班人数的关系。

[思考：本环节，用生活中的情境进一步帮助学生具体理解分数的意义。同时，学生用画图的方式直观地表示出对分数的理解，展示了思维的多元性。]

（三）基于动手操作，理解分数单位的度量属性

师说到分数，它发展到现在我们书写的样子，经历了漫长的时间。（出示图9）3000多年前，古埃及人在分物体时不能得到整数的结果，于是就用这样特殊的符号表示分数。猜猜这个分数是多少？

（学生猜测。教师揭示“14”，随后出示图10。）

师2000多年前，我国古代最初用算筹表示分数。看一看，这个分数是什么？

生25。

（教师揭示“25”，接着出示图11。）

师后来，印度人发明了数字，他们这样来表示分数。这个是——

生23。

（教师揭示“23”，随后出示图12。）

师公元12世纪，阿拉伯人发明了分数线，就把分数表示成现在这样了。从分数的发展史中我们不难看出，埃及是世界上最早使用分数的国家，但古埃及人在进行分数运算时，只使用分子为1的分数，因此这种分数也叫作埃及分数。

（出示图13。）

13、15、19、116……——埃及分数

师（出示图14）老师这里有一根彩色纸条，从中你发现埃及分数了吗？