简画图深思考，探规律建模型

“植树问题”是人教版五年级上册第七单元的内容，它是小学数学中一个经典的数学模型问题，它不仅涉及数学计算，还蕴含了丰富的数学思想和方法。教学目标旨在通过数学探究活动，使学生体会植树问题的规律，建构数学模型，并解决实际生活中的相关问题。教学重点在于发现并理解植树问题中间隔数与棵数的规律，难点在于应用这一解题思想解决生活中的实际问题。本节课我充分让学生通过数形结合的方法，理解在植树问题的各种情况中：“棵数”“间隔数”“间隔长”三者间的关系，并会应用本课学习的数学模型解决一些相关的实际问题。

一、在猜想中体会化繁为简

教师以“3月12日植树节”为引子，通过提问引导学生思考如何植树，从而引出“植树问题”。这种情境创设方式贴近学生生活，能够有效吸引学生的注意力，激发学生的学习兴趣。接着呈现教科书例1：同学们在长100 m的小路一边植树，每隔5 m栽一棵（两端都要栽）。一共要栽多少棵树？教师引导学生分析题意，借助课件帮助学生理解题目中的关键词：“小路一边”“每隔5 m栽一棵”“两端都要栽”，并鼓励学生进行猜测。由于猜测结果的不同，学生想到用画图来进行验证，但在实际操作过程中发现数据过大不便于操作。学生不难想到从简单情况入手进行研究，“化繁为简”的思想方法就能帮我们解决实际困难。此时教师引导学生思考，在间隔长5 m、两端都要栽这两个条件不变的情况下，选择多长的路来研究比较合适呢？4 m行吗？12 m呢？学生通过讨论发现：路长一定要是5的倍数才满足植树的要求，树与树的间隔长是5 m，路的起点和终点都要栽。

综上所述，这个环节通过情境创设、问题引导、关键词理解、猜测与验证以及思想方法渗透等多个方面，有效地激发了学生的学习兴趣，培养了他们的思维能力和解决问题的能力，同时还让他们掌握了重要的数学思想方法。即面对复杂问题时，先将其简化为易于处理的形式，再逐步求解。这一环节培养了学生的问题意识和初步的判断能力。

二、在数形结合中探究规律

为了引导学生理解“棵数”“间隔数”“间隔长”三者之间的关系，借助数形结合的思想，就能让学生找到间隔数与棵数间的规律，最终建立数学模型，为解决实际问题打下基础。

（一）画图探究，发现规律

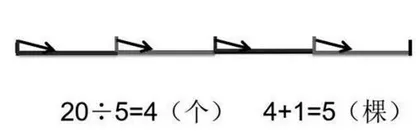
同学们共同思考：在20 m的路上，每间隔5 m栽一棵（两端都要栽），能栽几棵树？大部分学生能很快列出算式：①20÷5=4，②4+1=5，并能在线段图上进行验证确实是5棵树。但是当教师追问20÷5=4表示什么意思？谁能指着图说一说时就遇到了困难。接着教师就让同学小组合作讨论：4到底是什么？该带什么单位？很多同学说不清楚，也有很多同学认为4就是指4棵树。这时教师就引导学生从除法的意义出发：20 m的路是指路长，每5 m栽一棵是指间隔长，算式①20÷5=4是在求20 m的路长里面包含了几个5 m的间隔长？4其实是间隔的个数。算式②4+1=5（棵）同样让学生观察线段图，思考4、1、5分别表示什么？在图中的哪里？4棵树和4个间隔有什么关系？在一系列的问题引导下，学生通过思维碰撞，借助线段图，终于发现了间隔数和棵数是一一对应的关系。最后再抛出一个问题：4个间隔对应栽了4棵树，为什么还要加1呢？学生可以在线段图中把间隔和树一一对应着连起来，正好都是4，题目要求两端都要栽，所以终点（起点）这一棵也要栽，因此要加1。

这一环节通过教师的追问和引导，学生不仅得出了正确的答案，更重要的是深化了对问题的理解。线段图在这个环节中发挥了重要作用。学生通过观察线段图，将抽象的数学问题与具体的图形结合起来，更好地理解了问题的本质。同时，他们也学会了如何利用图形来辅助思考和解决问题。

（二）多组数据，验证猜想

如果只研究了20 m的路长，不足以支撑我们的猜想。所以鼓励学生用多组数据来验证，在作业单的引导下完成线段图并填写数据。最终根据学生的汇报形成一个表格，观察表格数据完成验证：（两端都栽）棵数=间隔数+1。最终解决了例1的问题，这条100 m的路上能栽21棵树。

这一环节通过验证猜想的普遍性培养科学探究精神、提升数据处理能力、增强图形与数值的结合能力、促进自主学习与合作学习，对学生的数学学习产生了积极的影响。它不仅让学生更深入地理解了植树问题的本质和规律，还让他们在数学学习中获得了更多的成就感和乐趣。

（三）拓展延伸，建立模型

当得出结论以后，教师就让男、女生分组在50 m的路上植树，应用结论每组应该栽树11棵，两个组加起来就是22棵，比刚才100 m路上能栽21棵多出了1棵。这就引发了学生的思考和讨论，结合线段图不难发现男生组的终点与女生组的起点重复了。教师就让男生组来栽这1棵重复的树，女生组的起点不用栽。观察女生组的线段图10个间隔对应10棵树，这种情况就是：（只栽一端）棵数=间隔数。接着教师提问：除了两端都栽、只栽一端，还会有其他情况吗？学生很快想到两端都不栽，结合课件就能观察发现：（两端都不栽）棵数=间隔数-1。

这一环节通过小组讨论、动手操作、合理推理等环节，学生逐步发现了植树问题的三种情况中的规律，建立了数学模型。这一过程培养了学生的实践操作能力和逻辑推理能力，拓展了学生的思维，为他们能够灵活应用所学知识解决实际问题打下基础。

三、回归生活，实际应用

当学生们经历了画图探究、猜想验证、建立模型这三个阶段后，紧接着出现了各种各样的练习题，有公交车站路线图题、环形公交车站路线图题、锯木头……为了发展学生的核心素养，还需要进行再一次的深度思考：①这些题目中没有树，那还属于植树问题吗？②应该如何解决这些问题呢？

此时让学生们展开全班讨论并总结：①看似没有树，但是都有相同的间隔长，所以属于植树问题。②路长÷间隔长=间隔数，两端都栽：棵数=间隔数+1；只栽一端：棵数=间隔数；两端都不栽：棵数=间隔数-1。植树问题三种情况的解题模型也形成了。

通过本节课的教学，学生不仅掌握了植树问题的规律，还学会了如何通过“化繁为简”“数形结合”的方法从简单问题中探索规律，通过线段图发现规律，找出解决问题的有效方法。同时，学生的模型思想和化归思想也得到了初步的培养。在教学过程中，教师注重引导学生动手操作、合作交流，使他们在探究过程中获得了成功的体验，增强了学习的自信心。此外，通过将植树问题应用于实际生活中，学生进一步感受到数学的魅力，提高了他们的学习兴趣和应用能力。