借助数形结合 呈现数学本质

数学是研究几何图形（几何）与数量关系（代数）的学科，教学中要借助图形、表格的描述，分析现实世界中存在的规律和现象，解决现实世界中的数学问题，学会从数学的视角观察、想象、思考，探究解决问题的策略，明确思考的路径，把握数学的本质。

一、“数”中觅形，代数知识几何化

“数”是指数学当中的数、符号、数量与数量关系等，它显得抽象、枯燥、理性、乏味;“形”是指数学当中的图形、线段、表格、数轴等，它显得形象、直观、感性、有趣。

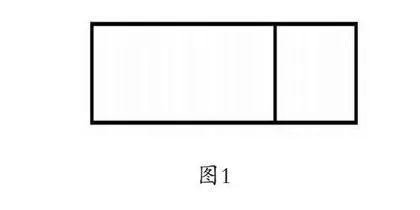
如，在教学“乘法分配律”一课时，可设计学生经历过的真实生活情境，学校的运动场长75米，宽25米，现在学校扩大办学规模，在宽不动的基础上，长增加25米，扩建后的运动场面积是多少？学生基本上存在两种方法：（75+25）×25和75×25+25×25，我们要结合几何图形来理解题意（如图1所示），每一步表示什么意义，分别是图形中的哪个部分，从而得出：（75+25）×25=75×25+25×25乘法分配律的雏形，通过几何图形理解概念和规律，加深印象，将代数的知识借用几何图形来理解算理，为接下来的进一步理解和研究乘法分配律的知识做好必要的铺垫。

再如，在五年级课本中有一道拓展练习题：（a+b）2=a2+

b2+2ab，涉及初中的知识二元二次方程，学生利用代数知识理解相当吃力，甚至连题意都看不懂，也为老师从学生现有的知识水平上去分析和讲解造成了困扰，如果我们能借助几何图形（如图2所示），就是两个交错的大小不同的正方形面积加上两个两侧一样的长方形面积，数学问题的解决就变得简单明了，直观易懂了。

二、形中探“数”，几何知识代数化

“没有什么东西比几何图形更容易印入脑际。”（笛卡尔语）数学教学追求数学知识图形化，也就是教学中要从特殊图形的探究中，将图表语言转化为数学的符号语言，推导出数学的一般性规律和通俗的结论，又可以运用所学到的数学规律和方法去解决生活中的数学问题。

如，教学“三角形的内角和”一课时，教师先从法国科学家帕斯卡的故事说起，12岁时帕斯卡问父亲：“什么是几何？”父亲轻描淡写地回答说：“几何就是教人在画图时能作出美观又正确的图。”于是帕斯卡就拿起粉笔在地上画起各种不同形状三角形的图形来。画着画着，帕斯卡受到启发，突然发现任何一个三角形的内角和都是180°。这节课，大家也将用自己的智慧，重走帕斯卡发现三角形内角和规律的道路，重新验证帕斯卡的结论，你们都有潜力成为帕斯卡一样的数学家。用故事调动学生学习兴趣，为学生树立了榜样，而且还教给了学生学习数学的方法，就是善于利用图形解决现实世界中的问题。这样的设计，学生就会产生研究的欲望，想去探索三角形内角和的数学奥秘。纸上得来终觉浅，绝知此事须躬行。接着我们引导学生动手量、撕、折、画、拼等不同的方法总结出形状不同的三角形内角和都是∠1+∠2+∠3=180°的结论。一切知识都是从感官开始的（夸美纽斯语），用多种感官参与到知识的认知、体检和感悟中，在研究直观的图形中得到数学结论，从形象走向抽象，从有趣走向理性，从看得见、摸得着的形象形体中抽象数学的知识和规律。最后教师不只满足于结论的得出，还因势利导地引导学生用学到的规律去发现更有奥妙的多边形内角和的方法。根据三角形的内角和的结论再利用，求四边形、五边形、六边形……n边形的内角和。通过图形添加辅助线，表格汇总，有助于观察总结结论，进一步升华了数学的规律，数学结论从特殊走向一般，培养学生数学的推理意识，去解决现实世界中的数学问题。（如图3所示）

数学教学中形中探数的例子比比皆是，在方格纸上画几何图形，在数轴中理解正负数的大小，利用集合图理解容斥问题，运用坐标图理解正反比例……，这些都是解决这类数学问题的灵丹妙药，只要学生能想到会用图表的策略，基本都能实现对症下药，实现药到病除的功效。

三、数形结合，数学知识模型化

数与形是数学的手和脚，是小学阶段非常重要的数学思想，撇开形与数进行学数学那是无源之水，无根之木，数学的道路很难走得远、走得久。它们是相辅相成、互相成就的。既要重视数形结合的几何因素——直观，更要重视数形结合思想——类比。

如，在教学五年级“分数加减混合计算”一课时，师出示喝牛奶问题：一杯纯牛奶，乐乐喝了一半后，觉得凉，就兑满热水。他又喝了一半，就出去玩了。乐乐一共喝了几杯纯牛奶？几杯水？

只要会读题，题中第一次喝了多少，地球人都知道，加满水也没问题，第二次在加满热水后，学生的思维就开始混乱了，牛奶与水混合在一起了，怎么区分哪里是热水哪里是牛奶，学生绕糊涂了，再加上要解决“杯的是多少”涉及六年级的分数乘法问题，学生还没学习呢。所以要突破这个难点就要借助图示来理解题意（如图4所示），通过画图，借助几何直观，用数形结合的方法，把水和奶完全隔离开来思考，结合直观图，理清题意，通过理解、观察、分析第二次喝了杯的一半是杯，加上第一次喝的杯就是牛奶喝了杯，水就喝了杯。

教学中还要引导学生用逆向思维进行反思和回顾，把喝的与没喝的牛奶加起来就能知道是不是一杯。

总之，数学知识的学习是永远无法绕开形与数进行研究的，它是数学学习中必不可少的基本元素，还是沟通代数与几何的重要桥梁，串联生活与数学的纽带，在代数知识的学习中，只要与形扯得上关系，就要发挥图形的作用，在几何图形的研究上，只要与数沾得上边，就要借助数来释义，当然两者结合互相转化，威力更不容小觑！正如华罗庚所说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休！”