几何画板助力初中数学教学案例研究
作者: 吴可可
摘要:在初中数学的教学实践中,我们其实可以借助几何画板帮助学生更好的理解数学的学习,比如,初中数学中的动点问题,函数问题,涉及到图形与几何的部分,我们都可以尝试着利用几何画板助力初中数学教学,帮助学生更好的掌握数学。针对此类较为抽象的数学题,如果从形的角度借助几何画板,可以更为直观的呈现数学的规律特点,这也体现了几何画板助力初中数学教学案例研究的优越性,而且,新课标也强调信息技术与数学教学的融合,几何画板作为信息技术下的产物,无疑发挥着重要的作用,而且有利于培养学生的数学核心素养。而培养和发展学生的数学核心素养,也是数学教学的目标要求,因此,我们非常有必要将几何画板引出数学知识的教学中,希望通过这些案例,能够给一线的数学教师们一些参考和借鉴,帮助教师探索如何提升学生数学核心素养的,探索更为有效的教学方式和途径来帮助学生数学核心素养的形成和发展。
关键词:数学核心素养
几何画板初中数学压轴题是区分层次和实现选拔的重要题型。由于压轴题考查的知识点较多,综合性较强,覆盖面较广,且关系复杂,思路难觅,解法灵活,常常令很多学生束手无策。其实解压轴题也是有一定的策略的。首先,图是压轴题的灵魂,结合图分析条件和结论是处理压轴题的首要工作;其次,要善于运用“通法”推进问
题的解答;最后,要掌握一些“类型问题”的一般解题思路。通过几何画板动态图演示,让同学们感悟“图”在解压轴题中的重要作用。下面以相似三角形存在性问题为例,借助几何画板进行探究,以期更好的辅助课堂教学,提升数学核心素养:
. .
, ( )
1. 90 2, 4
A A P x BEP y
PD AB AC D D A C E DC EPD
Rt ABC C BC AC P AB
设 、 两点的距离为 ,▲ 的面积为
交边 于点 点 与点 、 都不重合 ,点 是射线 上一点,且
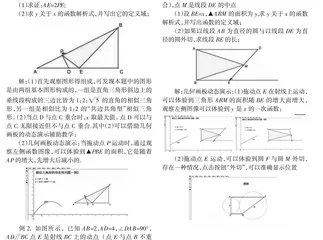
例 如图所示,在 ▲ 中, , ,点 是斜边 上的一个动点,
( )求 关于 的函数解析式,并写出它的定义域;
()求证: ;
y x
AE
2
1 2PE
解:(1)首先观察图形得组成,可发现本题中的图形是由两组基本图形构成的,
一组是直角三角形斜边上的垂线段构成的三边比皆为 1:2: 5 的直角的相似三
角形,另一组是相似比为 1:2 的“共边共角型”相似三角形.(2)当点 D 与点
C 重合时,x 取最大值。点 D 可以与点 C 无限接近但不与点 C 重合。其中(2)可
以借助几何画板的动态演示辅助教学:(2)几何画板动态演示:当拖动点P运动时,通过观察左侧函数图像,可以体验到
▲PBE的面积,它是随着AP的增大,先增大后减小的.
例2.如图所示,已知AB 2, AD 4,DAB 90,AD // BC.点E是射线BC上的动点
(点E与点B不重合),点M是线段DE的中点.
(1)设BE x,▲ABM的面积为y,求y关于x的函数解析式,并写出函数的定义域;
(2)如果以线段AB为直径的圆与以线段DE为直径的圆外切,求线段BE的长;
解:几何画板动态演示:(1)拖动点 E 在射线上运动,可以体验到三角形 ABM
的面积随 BE 的增大而增大,观察左侧图像可以体验到 y 是 x 的一次函数:
(2)拖动点 E 运动,可以体验到圆 F 与圆 M 外切,存在一种情况,点击按钮“外切”,可以准确显示位置虽然三角形存在性问题有一定“套路”可循,但大多数题目命题灵活,并无单一模式,对同学们提出了相当大的挑战。然而万变不离其宗,从特殊三角形本身的性质入手,结合边角的相互转化,就能拨开迷雾,探寻真相。通过几何画板的动态演示过程,动态的展现图形运动的全过程,给予学生更直观的感受。
参考文献:
【1】杨幸.几何画板融入初中数学教学的应用研究
【2】游淑溶.几何画板在初中数学教学中的实践应用分析[J].知识文库,2022(13):136-138.
【3】王丽.巧用几何画板,突破数形教学难点[J].河南教育(教师教育),2022(08):55.
【4】许小丽.运用几何画板辅助数学教学的实践与思考[J].科技信息,2010(30):314.
【5】张建文.借助几何画板,助力解题教学[J].教学考试,2021(29):49-53.
【6】王成杰,刘新春.重视性质教学,养育学科素养[J].中学数学月刊,2017(08):29-31.
【7】杨幸.几何画板融入初中数学教学的应用研究