谈数形结合思想在中职数学中的应用

【摘要】：数形结合，是将数学的两种表现形式——“代数”和“图形”有效地结合起来，互相补充，以达到解题的目的。作为数学解题中最基本的解题方法，数形结合思想在中职数学解题中得到了广泛运用，其主要用于解决函数问题、几何问题等。本文将对此两种应用展开探讨。

【关键词】：中职数学  数形结合  数学思想

一、 数形结合思想在函数问题中的应用

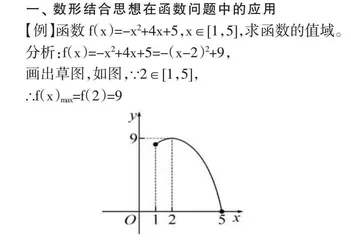
【例】函数f（x）＝－x²＋4x＋5，x∈[1，5]，求函数的值域。

分析：f（x）＝－x²＋4x＋5＝－（x－2）²＋9，

画出草图，如图，∵2∈[1，5]，

∴f（x）_max＝f（2）＝9

我们可以发现，这道例题是给定区间求二次函数的最值问题，需根据对称轴与给定区间的关系进行分类讨论，并结合函数单调性进行求解。切忌直接将区间端点值代入求最值。在解决二次函数有关问题时，数形结合的运用会使问题简单化，要养成良好的作图、识图、用图习惯。

二、数形结合思想在几何问题中的应用

相对于函数比较明显的“数”的特征，几何问题中则“形”的特征更为突出，数形结合的思想表现的较为典型，其充分表现在“以数解形”方面。

【例】如图，一艘轮船在工作点A处测得海上南偏东30°方向上有一口油井P，现以60海里/时的速度向南航行20分钟后到达B点时，测得油井P在其南偏东75°的方向上．试求油田P和工作点A之间的距离．

分析：由题意，AB＝60×＝20（海里），

由题意∠P＝75°－30°＝45°，∠PBA＝105°，

∴sin∠PBA＝sin（45°＋60°）＝，

∴由正弦定理得， ，

∴AP＝10（1＋）（海里）.

在解三角形的综合问题时，要仔细分析题目，结合图形，找出相应的三角形边角关系，灵活地运用正余弦定理，知识涉及面广，应用能力要求高.“以数解形”的解题方法不仅可以沟通数与形的内在联系，而且把代数式的精确性与几何图形的直观性描述有机地结合起来，达到优势互补的效果。

“数”、“形”是一个互译的过程，既是解题过程，又是学生的形象思维与抽象思维协同运用、互相促进、共同发展的过程。总之，在中职数学教学中，数形结合能不失时机地为学生提供恰当的形象材料，可以将抽象的数量关系具体化，把无形的解题思路形象化，不仅有利于学生高效率的学好数学知识，更有利于学生学习兴趣的培养、能力的增强，使教学收到事半功倍之效。

【参考文献】

1．吴海荣．数学新课程标准下教师有效教学行为分析．数学教育学报．2004．3

2．王冬平．促进学生有效学习的教学策略．中学数学教学参考．2009．10