基于大单元视角的微专题教学探究

《普通高中数学课程标准（2017年版2020年修订）》提出要培养学生数学核心素养，促进学生的发展．在此背景下指向整体教学的大单元教学应运而生.

核心素养下的数学大单元教学模式有以下三个特征：一是以拟定的大单元知识点为线索，对所涉及的教材内容进行科学疏理，形成知识网络，并消除章节间的不融洽;二是以大格局视角进行教学设计，开展主题研究，连通相关知识点，形成系统教学结构；三是通过大单元的整合教学对培养学生数学整体意识有很大益处，能引导学生对数学问题的整体思考，提升其逻辑思维能力和解题应用能力．

本文以二面角的教学为例，结合教学实践，对大单元教学模式的具体实施与安排进行探究．通过分析新课程标准对二面角的教学要求与近几年高考试卷中对于二面角问题的考查情况，设计出“二面角的求法”微专题，借此为高中教师进行二面角大单元教学提供些许建议．

本专题主要对人教A版必修二第八章立体几何初步与选择性必修一第一章空间向量与立体几何的内容进行了科学的梳理和整合，分别用平面角法、摄影面积法、向量法三种方法来解决二面角的相关问题。

一、平面角法

（一）定义法

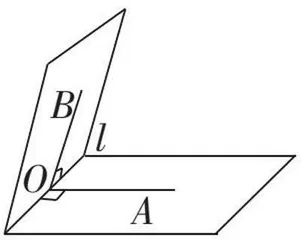
在二面角的棱上找一个点，在两个半平面内分别过该点做垂直于棱的射线，则两射线所夹的角为二面角的平面角. 如图所示，以二面角的棱上任意一点O为端点，在两个面内分别做垂直于的两条射线OA，OB，则AOB为此二面角的平面角.

例1  在三棱锥-中，，，求二面角的大小.

（二）三垂线法

从二面角的一个面上的一点向另外一个面做垂线，再由垂足向公共棱做垂线，得到棱上一点，即斜足，斜足与面上一点的连线与斜足和垂足的连线所夹的角即为二面角的平面角.如图所示，在平面内选一点A向另一个平面做垂线AB，垂足为B. 再过点B向棱做垂线BO，垂足为O，连接AO，则角AOB是二面角的平面角.

例2  在四棱锥中，为平行四边形，，，求二面角的正切值.

（三）垂面法

过空间一点，作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角.如图所示，过空间一点做平面垂直棱于点，交平面于，交平面于，则就是二面角的平面角.

例3  在四棱锥中，为正方形，，，求二面角的大小.

二、摄影面积法

已知平面内一个多边形的面积为，它在平面内的射影图形的面积为，若平面和平面所成二面角为，则，此方法可简便的求解无棱的二面角问题.

例 4  在正三棱柱中，为中点，且  ，求平面与平面所称锐二面角的度数.

三、向量法

如图，平面与平面相交，形成四个二面角，我们把这四个二面角中不大于的二面角称为平面与平面的夹角.若平面与平面的法向量分别是和，则平面与平面的夹角即为向量和的夹角或其补角.设平面与平面的夹角为，则.

我们可以利用两个平面夹角求二面角.记两个平面所成角为，两个相应半平面所成角为.若，则，若，则.

例5  四棱柱为长方体，，点，分别为，的中点，求平面与平面夹角的余弦值.

【课题项目】

济源市基础教育教学研究室2023年度立项课题——基于学科核心素养的高中数学单元整体教学的实践研究

河南省基础教育课程与教学发展中心2023年度立项课题——指向深度学习的高中数学单元整体教学的研究