“合并抵消”大概念统摄下的运算律教学

“合并抵消”大概念统摄下的运算律教学0

一、单元视角：单元要学什么

学生四年级学习《运算律》之前，已经学过乘加、乘减等两步四则混合运算及有小括号的运算，后续还要学习小数、分数混合运算。学习本单元前对运算律有所体会，但未正式学习。学完运算律，后续还要在小数、分数领域应用。

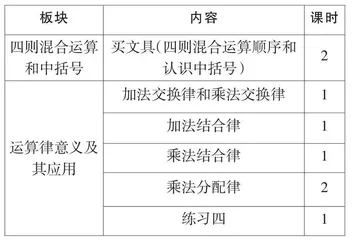
本单元共安排8课时学习，分别是四则混合运算顺序和认识中括号，加法交换律和乘法交换律，加法结合律，乘法结合律，乘法分配律和练习四。

纵观8课时，无非2个板块，一个是关于四则混合运算和中括号；一个是关于运算律意义及应用。由此可见，对于混合运算板块学生有丰富的学习经验，而对于运算律板块学生第一次正式学习。

二、学生立场：有哪些学习节点

（一）学情分析

在教学中，我们发现学生对混合运算掌握较好，两步混合运算顺序和法则可以直接迁移到三步混合运算。而运算律这块，学生出现问题较多，掌握不扎实。学生出现的典型错误主要有：

错例A：

错因分析：不能凑整的算成凑整。学生受数字特征的负迁移，忽视了运算顺序。

错例B：

错因分析：学生或没有观察数字特征，或不能灵活运用运算律。

错例C：

错因分析：学生忽视运算符号，混淆乘法结合律和乘法分配律。

当学生学完整个单元的运算律后，各运算律更加容易混淆。随着算式的变化，学生出现的错误更是五花八门。

（二）教材解读

面对学生的错题，我们往往会认为缺少训练，通常用题海战术巩固，很少会追根溯源。这些错题真正的根源在于缺失运算律意义的理解。究其原因，我们认为教材编排中对算理、算法和算律的定位有值得商榷之处。

我们知道，算理和算法在一起，算理是解决为什么可以得到这个计算结果的问题。算法是对算理熟能生巧后的概况，怎么得到这个结果。所以，算理解决“对”的问题，算法解决“快”的问题。算法和算理在一起，算法是怎么可以得到这个结果。算律是怎么可以比较快地得到这个结果。算法解决“对”的问题，算律解决“快”的问题。因此，算律是对算法的一次叛逆。

学生先学习算理，再学习算法，最后学习算律。算律的学习，必须向着学生的痛点而行，这个痛点正是算律的意义所在。如学习加法交换律和乘法交换律，教材都是呈现两个数相加或相乘等于交换位置后的得数，这样引出交换律，引导学生经历探究规律并运用规律，从形上理解运算律，不利于理解运算律的意义，导致运算与运算律脱节。如果材料改成三个数连加，当第一个和第三个数能凑整，让学生充分体会换位的必要性，交换律这样上会形神兼备。通过交换位置，改变运算顺序，但得数没变，从而深刻理解运算律的意义。

（三）课标理解

《新课标》对运算律提出了两方面的要求：一是探索并理解运算律（加法交换律和结合律、乘法交换律和结合律、乘法对加法的分配律），能用字母表示运算律。二是能运用运算律进行简便运算，解决相关的简单实际问题，形成运算能力。

一是从运算、解决问题两个目标看，要合理开展结构化学习。二是运算律作为一种数学思想的高度教学，建立“合并和抵消”的运算思想。同类事件，可交换顺序再做，但不改变事件的本质。合并思想就是相同的事合并做，抵消思想就是不同的事抵消做。

综上，我们发现加法乘法交换律、加法乘法结合律、乘法分配律都经历了情境引入、发现规律和应用规律，更多停留在“形”上理解运算律，让人感觉有形无神。我们认为可以从算法到算律，以猜想、推理、验证的方式，把在加减法中认识到的运算思想推及乘除运算，形成运算的结构化知识，同时也符合学生认知，更能形神兼备。

三、结构整合：怎样整合和拓展

基于以上思考，我们认为可以这样整合和拓展：

一是把加法交换律和加法结合律整合成一节课，乘法交换律和乘法结合律整合成一节课。交换律都是交换位置改变运算顺序，结合律是先算后面，再算前面，也是改变运算顺序。本质上都是改变连加的运算顺序，道理是一致的。理解改变依据就是三个数连加的意义，运算顺序变了得数不变，这样来理解运算律的意义。不同的是第一个内容是连加运算，第二个内容是连乘运算。学生掌握了加法运算律，自然会迁移到乘法运算律，推进结构化学习。

二是增加一节减法和除法运算性质的拓展课。学完加法、乘法的交换律和结合律，学生自然而然会继续想减法、除法中有没有运算律。小学阶段，减法性质类似减法的结合律，除法性质类似除法的结合律。

三是保留《四则混合运算顺序和认识中括号》、《乘法分配律》和单元练习课。

整合前8课时，整合后还是8课时。虽然课时一样，但里面的内涵不同，学生对运算律的理解更加到位。

四、关键课例：大概念统摄下的单元教学

《加法运算律》是重点课，《乘法分配律》是难点课。现在我们将《加法运算律》这节课作为关键课例进行分析。首先确定教学目标：

知识点：对材料进行讨论发现，在理解运算律的意义中认识运算律，并会用字母表示。

技能点：能把运算规律用自己的语言表达，能运用运算律巧算，解决简单的实际问题，体会巧算的方便。

体验点：加强对运算律的理解，体会加减法同级运算律为一个整体，形成“合并抵消”运算思想。

教学过程：

（一）情境引入，形成素材

选材：老师手中有10颗糖，淘气又给了老师4颗，笑笑也给了老师3颗。老师现在有几颗糖？

1.可以怎么列算式？

10+4+3 10+3+4 10+（4+3）

2.为什么可以这样列式？说一说表示什么意思？

3.你能结合情境再举一些像这样的例子吗？

15+5+6 15+6+5 15+（5+6）

20+4+8 20+8+4 20+（4+8）

……

【设计意图：用拿糖的事导入新课。让学生非常清晰的感知老师拿进糖与加上一个数的联系，并联系生活其他情景举例，为探索运算律感受运算思想提供学习素材，以及充分的探讨做准备，感受混合运算是对解决问题程序的一种综合记录。】

（二）讨论素材，形成结构

选材：

10+4+3 10+3+4 10+（4+3）

15+5+6 15+6+5 15+（5+6）

20+4+8 20+8+4 20+（4+8）

……

1.仔细观察上面的素材，小组讨论发现了什么？

第一问：什么没变？让生明白，运算结果不变，事件也没，都是拿进糖。

第二问：什么变了？事件的先后顺序变了，交换了一下事件的先后顺序。

第三问：这样的变都可以吗，因为不管怎么变，其结果不受影响。

2.用字母表示规律：a+b+c=a+c+b=a+（b+c）

3.引出运算律

像这样的a+b+c=a+c+b我们称为加法交换律。

像这样的a+b+c=a+（b+c）我们称为加法结合律。

【设计意图：以现实素材为背景，帮助孩子在现实情境中理解领会运算思想，感受交换、合并只是事件的先后顺序发生了改变，结果并没有变化，从“形式”探究走向“意义”建构。】

4.感受运算律的简便

在我们小学四年的学习中，以前有遇到过吗？（出示书本素材）

三上第18页，捐书活动（三位数连加）中出现：727+114+86

三上第22页，结余多少钱中出现：653+97+203

第一问：三年级时按顺序算是怎么算的？

第二问：现在你觉得还可以怎么算？

第三问：为什么按顺序算不方面？

第四问：为什么用了运算律后变简便了？

小结：看来用上加法交换律或结合律后，可以使得计算变得更简便。

【设计意图：通过具体例子，感受交换律、结合律带来的计算便捷。】

5.小练习：快速算

27+95+73 27+95+105 27+95+84

问题一：所有的加法计算都能用运算律后变简便吗？

问题二：什么时候能用交换律、结合律？什么时候不能用？

再次小结：使用加法交换律、结合律时，要考虑数字特征，当当交换或合并起来刚好是整十、整百数的时候我们才会去运用，才会起到简便计算的效果。

【设计意图：为什么要交换、合并？基于对数字特征的需要，当交换或合并起来刚好是整十、整百数的时候我们才会去合并。所以合并的前提是数字的特征需要，而且交换、合并前与合并后计算结果是不变的。让学生感受到思想模型的产生是为了方便计算。】

（三）猜想拓展，减法延伸

1.问题一：是否在看到能凑整十、整百数时，就能去凑去用运算律。

举例：314-198+2

能否用结合律变成314-（198+2）？为什么？

生：不能，计算结果不同，因为有减法，没有减法结合律。

尝试用糖果的情境来说一说两个算式为什么不同。

2.追问问题二：那是不是有减法的同级运算就不能用交换律、结合律？

举例：376+85-76 273-79-73 314-198-2

仔细观察算式能否简便计算？

结合分糖果的情境说一说为什么可以用交换律和结合律。

前两个例子：让学生明白，运算结果不变，事件也没，都是拿进或者拿出糖。我们在用交换律时，要带着符号换位置，符号是方向，也是事件的性质，交换后只是事件的先后顺序变了。如果不带着符号换位置，事件就会发生改变，例如+4表示拿进4颗，而-4表示拿出4 颗。

第三个例子：这题是孩子们比较熟悉的，在连减中可以先把减数先相加，再一起减掉，也就是相同的事可以合并做。

3.小结：在加减同级运算中，交换律就是：带着符号换位置，只是改变了事件发生的先后顺序。结合律：如果都是加，可以先把后面加数合起来再加，如果都是减，可以先把后面减数合起来再一起减，也就是相同事情合并做。

【设计意图：从连加拓展到加减混合运算，感受减法中也有运算律。符号+数字，符号是方向，也是事件的性质，数字是数量，也是事件的程度（我们可以称其为“向量”），在不改变结果的前提下，我们可以改变事件发生的序，但是绝对不能改变事件发生的方向和数量，表现在记录上就是：带着符号换位置。】

（四）提出思考，有效迁移

加减同级运算中，存在着交换律、结合律，想一想乘除法同级运算中，有这样的规律吗？他又会是怎么样的呢？我们下一次再一起研究。