纸上得来终觉浅 绝知此事要躬行

94年大学毕业后一直从事农村教育工作。当被通知教学小学数学，不禁哑然一笑，随之有一种大材小用的感觉。然涉入课堂还没几节课，便感觉茫然起来：课本知识，一目了然，自觉寥寥几句就可讲完。初以为本人言简意赅、提纲挈领，洋洋还没来得及得意，一次次学生的作业、单元测试彻底颠覆了我原来的自信与憧憬！沉默！沉默！依然沉默！

不在沉默中爆发，就在沉默中灭亡！反思，学习，探索，再反思，总结，再反思，再总结...。冷静下来重温大学老师的谆谆教导，豁然开朗的感觉扑面而来...。

既没有高大上的理论依据，也没有科学、具体、华丽的数据，开门见山，把自己教学中的点滴感悟、些许经验（教训）全盘托出。期盼您的批评与指正！

众所周知，小学数学图形教学是一个难点。三角形、长方形、正方形、梯形、圆、长方体、正方体、圆柱的周长、面积、体积公式。诸如

1、长方形的周长=（长+宽）×2 C=（a+b）×2

2、正方形的周长=边长×4 C=4a

3、长方形的面积=长×宽 S=ab

4、正方形的面积=边长×边长 S=a.a= a

5、三角形的面积=底×高÷2 S=ah÷2

6、平行四边形的面积=底×高 S=ah

7、梯形的面积=（上底+下底）×高÷2 S=（a＋b）h÷2

8、直径=半径×2 d=2r 半径=直径÷2 r= d÷2

9、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr

10、圆的面积=圆周率×半径×半径 ？=πr

11、长方体的表面积=（长×宽+长×高＋宽×高）×2

12、长方体的体积 =长×宽×高 V =abh

13、正方体的表面积=棱长×棱长×6 S =6a

14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a

15、圆柱的侧面积=底面圆的周长×高 S=ch

16、圆柱的表面积=上下底面面积+侧面积

S=2πr +2πrh=2π（d÷2） +2π（d÷2）h=2π（C÷2÷π） +Ch

17、圆柱的体积=底面积×高 V=Sh

V=πr h=π（d÷2） h=π（C÷2÷π） h

18、圆锥的体积=底面积×高÷3

V=Sh÷3=πr h÷3=π（d÷2） h÷3=π（C÷2÷π） h÷3

尤其是在图形教学方面。例如在长方形教学过程中，首先让学生手工制作长方形。在制作的过程中，充分感受长、宽分别相等，长方形的周长，长方形的面积等。

一注重过程更注重方法。

二化繁为简，尽量用简单、通俗易懂、贴近生活、学生感兴趣的方式教学，往往事半功倍，起到意想不到的效果！

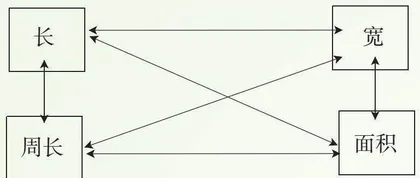
例1：长方形问题：长a，宽b，周长c，面积s

小学数学长方形问题涉及长a、宽b、周长c、面积s四要素。已知其中任何两项，即可求其他两项。①引导学生课下用下棋方式进行游戏，自行制定规则，激发学生学习的兴趣。②引导学生归纳出长方形考查有几种题型。如：已知a，b求c，s;已知a，c求b，s;已知a，s求b，c;已知b，c求a，s;已知b，s求a，c;已知c，s求a，b.③学生自主设计关于长方形的测试题，用于各小组之间竞赛，量化管理，激发小组内互帮互助，小组之间相互竞争。

例2：圆的问题

小学数学涉及半径r、直径d、周长c、面积s四个要素。已知其中任何一项，即可求出其他各项。①引导学生课下用下棋方式进行游戏，自行制定规则，激发学生学习的兴趣。②引导学生归纳出圆形考查有几种题型。如：已知r求d，c，s;已知d求r，c，s;已知c求r，d，s;已知s求r，d，c.③学生自主设计关于圆形的测试题，用于各小组之间竞赛，量化管理，激发小组内互帮互助，小组之间相互竞争。

此类方法不仅可用于图形中，也可以用于数的计算中。

例3：a+b=c  中，已知其中任何两项，即可求另外一项。

b=c  中，已知其中任何两项，即可求另外一项。

a×b=c  中，已知其中任何两项，即可求另外一项。

a÷b=c  中，已知其中任何两项，即可求另外一项。

三在抓好基础知识与技能的基础上，还要抓好学生的逻辑推理能力、思维能力。

（一）高年级小学生的思维特征

1、 在五、六年级小学生正处于高年级阶段，他们的思维主要有以下几个特点：①思维材料和方式发生了变化，这为中高年级学生从具体形象思维逐步向抽象思维过渡准备了条件。②思维品质有所发展，辩证思维开始出现，这为中高年级学生思维能力的形成提供了可能性。

2、思维品质的差异，为思维能力的提高提供了空间。由于心智的发展和教育的各种因素影响，学生的思维品质开始出现分化，主要表现为：①是学生思考问题时主动思维倾向存在，但是不能很快进入思维状态，还没有形成一个良好的思维习惯，缺乏正确思维方法；②是数学知识是按一定的内在联系组织在一起的，学生还不能对所学知识形成一个系统的认识和理解。

（二）、培养高年级小学生数学思维能力的措施

1、通过课堂授课，培养学生分析问题的思维能力

在学习新课时，教师要重视对学生 操作感与知识迁移的指导，要加强从知识整体与局部分别设计有坡度、有层次、有启发性并且符合学生认识规律的系列问题，让学生亲身经历探索新知识的思维过程，引导学生自己发现问题、分析问题并得出结论，发现新知规律，从而培养其学习能力，发展其智力。

2、通过让学生独立思考，培养学生判断、推理问题的思维能力

培养学生初步逻辑思维能力的过程即是培养学生有根据、有条理地进行思考后能完整地叙述 自己思考的过程以及说明理由的过程。而培养学生有根据、有条理思维的关键是不断提高学生思维的逻辑性，让学生学会思考。学生体会到思考的乐趣，就会养成独立思考的习惯。

3、及时反馈，思维总结

学生的成绩最大的误区。不是自己的能力问题，知识的掌握多少，而是不从失败中引起重视，不及时总结，究竟错在哪里，为什么错，都要弄个水落石出，方能找出原因，得以巩固知识。

以上只是本人在一线工作的粗浅体会，希望各位同行不吝赐教，本人抛砖引玉的愿望也就达到了。

做一名有思想的教育者，让我们共同行动起来！