教学支架在小学数学教学中的应用策略

摘 要 在新课程改革背景下，教师如何应对新版本教材的变化是对教师提出的新课题、新挑战。以苏教版“分与合”内容变化为例，探讨了教学支架的两面性，并提出教学支架的应用策略，主要包括：何时需要教学支架、如何搭建教学支架、如何拆除教学支架。

关键词 小学数学 教学支架 应用策略 “分与合”内容

一、新旧版本教材中“分与合”内容的变化

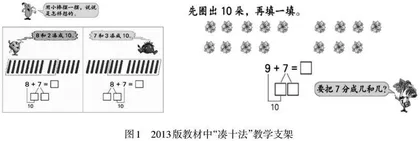
2024秋季，义务教育开始使用新版教材。与旧版教材相比较，在新苏教版《义务教育教科书·数学》中“分与合”内容有所变化。第一，在2013版教材中，“分与合”内容单独成章；而2024版教材中“分与合”内容不再单独成章。第二，在2013版教材中，“20以内的进位加法”内容提供了“凑十法”教学支架，如图1所示；而2024版教材中没有出现“凑十法”教学支架。[1]

与2013版教材相比较，2024版教材弱化了“分与合”内容。这种弱化是基于教学理念、课程结构、教学方法、学生发展等方面综合考量的结果。教师应该积极关注、深入思考并采取科学的对策。本文仅从教学支架角度对此进行分析。

二、教学支架对学生发展的两面性

教学支架是指在教学过程中，通过提供适当的支持和指导，帮助学生逐步掌握知识、技能和方法。它强调的是教师在教学过程中的引导作用，让学生能够通过逐步的、有层次的学习过程，最终独立掌握所学内容。

（一）教学支架促进学生掌握方法

应用教学支架的积极意义是明确的，如促进学生理解知识、提高学习效率、改善课堂氛围、满足个性化需求等。教学支架注重发挥学生的学习主体地位，让学生的能力素养得到提升。[2]在一年级数学中，“分与合”内容是学生学习数学的基础知识之一。其中包括数的分解与组合，将一个数字分解成几个小数字的和，或者把几个小数字合并成一个大的数字；还包括对加减法的基础性支持，通过分解与组合概念帮助学生理解和掌握基本的加减法运算。从本质上看，这些内容不是单纯的知识传授，而是一种教学支架。通过这种教学方式，教师可以有效地引导学生掌握基础的数学概念和运算方法，为后续的数学学习打下坚实的基础。

（二）教学支架限制学生思维发展

教学支架旨在引导学生学习，但是如果设计不当或机械应用，可能会限制学生的创造性思维和想象力的发展。学生可能会被固定的条框所束缚，难以产生新颖的想法和观点。例如，在“9加几”教学中，如果过于聚焦分与合思路，则数形结合、模型意识等思考问题的方法可能被淡化，还可能在后续学习中，在看规律想结果、代数思想启蒙等创新内容学习时难以绽放出思维火花。

思维限制往往伴生着过度依赖。如果学生过度依赖教学支架，可能会削弱他们的自主学习能力和解决问题能力。长此以往，学生会习惯于依赖外部支持，在进位加法学习中出现“见进位就拆数”的狭隘思维惯性，缺乏独立思考和探索的科学精神。

三、教学支架的应用策略

支架是一种定型框架，它铺平了道路，也造就了道路的惯性。思维惯性是学生创新的主要障碍，影响学生的思维培育。在学习过程中，教师要指引学生学会从问题解决的源头和起点寻找新的思维路径。

（一）何时需要教学支架

支架内容存在于课堂教学之中，根本上源于课堂教学内容矛盾体的不断变化。课堂教学发展进程中，各教学要素矛盾体之间不断演变，包括知识或技能发展过程中的矛盾、思维矛盾、学习个体差异矛盾等，矛盾体之间的对立统一决定着支架存在与否的意义。

1.原有方法应用效率低下或失效。例如，在学习10以内的加减法时，学生往往是采用“点数”方法。“点数”一般分为两个计数策略阶段，当总和等于或小于5时，学生往往源于直观，如3加2，当真实物体摆出来时，头脑中能直接合成整体“画面”，直接感知出和是5，无须“点数”；当总和超过5时，最本能的策略是按序点数，但是数量越大，点数的困难越大，速度越慢、越容易出错，已有经验与问题解决需求的冲突明显呈现出来，矛盾由此产生。

2.需要新的思维方式解决新问题。例如，9 + 4 = ？第一，结果13为什么不是一位数，而是两位数？学生需要实现从“无进位”到“有进位”的认知突破。第二，思维认识与数学表征的矛盾，学生把9个、4个合起来数，能数出来13个，但是学生心中的“口语13”，数学符号记录为什么是两个数字组成的“13”，而不是一个数字符号？这里有数的位值构造规则问题，学生没有这样的规则认知储备，形成了心理认知与数学表达之间的矛盾。

（二）如何搭建教学支架

随着学习的深入和学生能力的提高，原本存在的矛盾体可能会逐渐消失或转化为新的矛盾体，教师需要根据矛盾体的演变过程动态调整支架的类型和程度。这种调整既包括对已有支架的优化改进，也包括根据新出现的矛盾体设置新支架。教学支架的设置要符合学生的心理认知规律、符合教学内容特征、符合教学规律。皮亚杰的认知发展理论认为，人的认知发展具有阶段性和不可逾越性。小学生思维的主要特征是具象性，即离不开具体事物的支撑，同时随着年龄的增长，也逐渐出现抽象思维意识。在实际教学中，教师还需要结合教学内容的特征规律，设置有针对性的支架。

1.结合教学内容设置不同的教学支架。例如，在学习10以内、20以内加减法时，教师需要采取不同的支架策略，学习10以内加减法时，可以通过点数手指、小棒等实物的形式实现，而学习20以内加减法时，学生需要认识10在加减法运算过程中的特殊地位，通过10的分解和组合实现简化计算的目的。

2.借助10的特殊性转换思维方式。例如，数的加减运算是十进位，当个位上总数超过10时，就需要换成十位上的“1”。如用10个球装满1整盒、10个小棒成1捆、10朵花为一个集合等。

3.创设流程图支架形成结构化图示。教材中虽然弱化了“凑十法”教学支架，但是对于初学者，“凑十法”支架仍然具有重要价值，是培养学生学会十进位的重要方法。在教学过程中，教师需要根据学生的实际情况，适时进行使用。

4.多种支架并用促进思维进阶。例如，通过点数、摆小棒、圈一圈、流程图等进行运算后，通过语言型支架引导学生持续思考。你最喜欢哪种方法？哪种方法效率最高？或者通过情感型支架激发学生情感参与，让学生说出心中的疑惑，鼓励学生说出心中的好奇，参与实践调动积极性等。

（三）如何拆除教学支架

教学支架对学生学习起到支持、引导和辅助等作用，对教学效果具有促进作用。课堂教学中的矛盾状态瞬息万变，所以教师需要根据实际情况动态调整教学支架。

1.逐渐减少过程提示，最终实现完全独立。在学生已经掌握了基本概念和技能后，教师可以逐渐减少对解题步骤的提示和指导，鼓励学生尝试独立思考和解决问题。例如，从最初的详细步骤演示，逐步过渡到只给出关键步骤或提示，最终让学生独立完成。

2.提升知识难度，揭示知识本质。随着学生能力的提升，教师应适当增加问题的难度，改变知识、技能呈现的载体方式，挑战学生的现有发展水平，直面新的“最近发展区”。例如，在“9加几”教学中，当学生能用10个小棒捆成1捆、10朵花为一个集合等方法时，要基于这些表象，正式引导进入流程图表达，把不同的操作过程用统一的流程概括出来，归纳出共性，揭示出本质。

3.同伴协同互助，填补思维空隙。组织学生进行小组讨论和合作学习，各自说说不同的“凑十”方法，让他们在交流中相互启发、共同进步。通过小组活动，学生可以从同伴那里获得“他山之玉”，填补思维缝隙。学习伙伴的互补性，是预防思维方式单一聚焦、一枝独秀的有效方式。

4.基于个体差异，实施差异教学。基于学生不同的学习能力和认知水平，教师应根据学生的个性化差异搭建不同跨度的教学支架。同样是进位加法，对于基础较好的学生，可以较快地拆除支架，如学完“9加几”“8加几”就不再呈现流程图；而对于需要更多帮助的学生，则应保持一定的支持，流程图可能存在很长时间。

教学过程永远是矛盾体对立与统一、整合与重生的发展过程，这一过程会应用到不同的教学支架。支架的内容与形式、出现与隐退的时机等都应该基于教学因素的矛盾特点来考虑。教师需要引导学生通过分析矛盾，寻找解决策略。

[参 考 文 献]

[1]孙丽谷，王林.义务教育教科书·数学（一年级·上册）[M].南京：江苏凤凰出版传媒集团，2013：88-93.

[2]孙芸.搭建教学支架，筑造精彩舞台：初中数学支架式教学的实践探索[J].数学大世界（上旬），2023（11）：98-100.

（责任编辑：姜显光）