一种改进的折线逼近算法在建筑物轮廓线规则化中的应用研究

摘要：建筑物轮廓线的规则化是提取建筑物形状信息的重要步骤，文章对多边形建筑物轮廓线规则化进行研究，采用折线逼近算法以及改进后的折线逼近算法分别对多边形建筑物轮廓线进行规则化试验，实验结果表明，基于轮廓曲率角点的折线逼近算法能够有效规则化建筑物轮廓线。

关键词：折线逼近；轮廓曲率角点；建筑物轮廓线；规则化

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2025）06 -0131-03开放科学（资源服务）标识码（OSID）：

0引言

目前，多边形建筑物轮廓线规则化的算法主要基于最小拟合误差原则进行形状逼近，主要有两种方法：首先是折线逼近算法，在满足精度要求的前提下，通过多段折线实现最佳逼近[1]；其次是利用多边形的角点，通过提取多边形轮廓线的特征角点，重建多边形轮廓线[2]。

关于建筑物轮廓线规则化研究，很多学者采用先计算建筑物的主导方向，再判断主导方向是否与建筑物的边缘轮廓线正交，最后利用正交约束，直角约束等条件进行处理。此种方法对于没有正交关系的建筑物轮廓线效果不佳。例如吴秀芸[3]采用的算法只适用于规则形状的建筑物轮廓线。本文采用结合基于轮廓曲率检测角点的折线逼近算法进行建筑物轮廓线规则化的应用研究。

建筑物轮廓线多为多边形，多边形可以用一个二元组来表示：M=（K，V），二元组中V是多边形上全部顶点的集合；K是M中拓扑连接关系的集合，且每个顶点有且只有两条邻边。对于已知的多边形，其轮廓线简化原则是需要尽量保证简化后的多边形与已知的多边形在形状上保持一致，在此前提条件下，减少顶点或角点个数。

1建筑物轮廓线链码跟踪

利用折线逼近算法进行轮廓线规则化之前，先要得到轮廓点，再使用折线逼近算法进行建筑物轮廓线的规则化。在计算机中，物体的边界由多个相邻的像素点表示。一条曲线可以用曲线遍历的起始点和各边界点的方向码值进行定义，此方法被称为链码表示法。链码根据中心像素点的邻接方向分为4连通链码和8连通链码[4]。

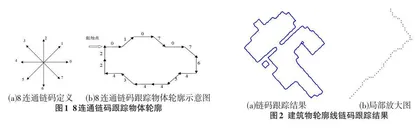
本文利用8连通链码轮廓线跟踪算法来跟踪边界线，8连通链码表示任意一个像素周围均有8个邻接点，与像素点的实际相符。8连通链码跟踪物体轮廓的示意图如图1所示。

建筑物轮廓线一般是封闭的连通区域，分别对多个连通区域进行标记并依次逐个跟踪，本文8连通链码的轮廓跟踪具体步骤如下。

1）按照顺序遍历建筑物轮廓图像，最小行值和最小列值作为首个轮廓起始点，定义扫描方向变量a，变量用来记录遍历轮廓点的移动方向，初始值为7；

2）按照逆时针方向搜索当前像素周围3×3邻域的范围，对于8连通区域，若扫描方向变量a 为奇数，取（a+7）mod 8；若a为偶数，取（a+6）mod 8，本文实验扫描方向变量a 的起始值为7；在3×3邻域中遍历搜索到的第一个点与当前像素值相同的像素点，则认为是新的边界轮廓点n，与此同时，变更扫描方向变量a 作为新的方向值。

3）如果点n 等于第二个边界点，并且前一个边界点n-1等于第一个边界点，就停止搜索，完成链码跟踪，否则继续进行第2个步骤继续进行链码跟踪；

4）最后将由边界点0、1、2......构成链码跟踪边界。利用实验数据，通过轮廓线的8邻域链码跟踪得到的轮廓点如图2所示，图2（a）中表示跟踪的边界轮廓点，图2（b）是局部放大图。

2折线逼近算法

折线逼近算法旨在利用少数关键点或特征点对多边形进行拟合，在保证物体轮廓线特征的情况下，最大限度地减少轮廓线的数据量[5]。国内外学者做过相关研究，如Ray的顺序法[6]、Dinesh和Damle的分裂融合法[7]、Carnona Poyato 和Fernadez Garcia 的支配点检测法[8]、Shu和Luo的基于几何矩计算的方法[9]等。该算法通过多段直线拟合不规则曲线，对于检测出来的轮廓点，进行折线最佳逼近，得到较规则的图形。

折线逼近算法用于二维平面中给定的一个由N 个点组成的数字轮廓曲线，从这N个点中，选出M个点组成新的多边形，由最终的多边形来代表原始轮廓线[10]。在利用链码跟踪算法对建筑物轮廓线进行跟踪之后，根据得到的轮廓点进行折线逼近，折线逼近算法的原理示意图如图3所示。

折线逼近算法的步骤如下：

1）首先确定阈值ε，用于判断点到直线的距离与阈值ε 的大小关系。

2）在同一连通区域内，对轮廓线上的点进行折线逼近，对每条轮廓线上首尾两点连成一条直线，成为基准线，求出所有点与基准线的距离，并找出距离的最大值d_max，比较d_max 与阈值ε 的大小。如果d_max<ε，则删除曲线上中间的所有点，首尾两点的连线即为折线逼近结果。如果存在d_max≥ε，则将距离基准线最远的点标记为第i个点，删除基准线，并将第一个点和第i个点，以及第i个点和最后一个点连线，形成的新的基准线，如图3中的直线P₁P_i 和直线P_iP_j 即为形成的新的基准线。

3）重复步骤（2），继续计算折线上的点到新的基准线的距离，并判断距离的最大值d_max 与ε 的大小关系。直到所有的点到基准线的距离都小于ε 时，保留的基线即为折线逼近的结果。

通过链码跟踪的轮廓点数据进行折线逼近拟合建筑物轮廓线，为了能够得到较规则的轮廓线结果，文中对折线逼近的结果进行了平滑处理，实验结果如图4所示。实验可知，运用折线逼近算法进行轮廓线规则化，能够得到平滑的建筑物轮廓线，但轮廓线直角处同时被平滑，最终会存在直角圆弧化的现象。算法忽略了轮廓线角点的重要作用，所以直接用折线逼近算法得到的结果不能够满足建筑物轮廓线规则化的要求。

3基于轮廓曲率角点的折线逼近

为解决上述问题，采用基于轮廓曲率检测角点的折线逼近算法进行建筑物轮廓线的规则化。基于轮廓曲率的多边形角点检测算法[11]一文已明确物体的形状是反映物体特性的关键因素，形状信息是通过形状的边界轮廓线来反映，而最能反映轮廓线特性的是轮廓线上曲率变化较大的点，即角点。

基于轮廓曲率角点的折线逼近算法是利用基于轮廓曲率角点检测算法检测出来的图像角点进行限制，设定角点分别为（x₁ ，y₁），（x₂ ，y₂），……（x_n ，y_n），首先查找图形的连通区域，若存在多个连通区域，分别对连通区域进行标记，然后依次对每个连通区域内相邻的轮廓角点作为折线逼近的首尾两点，连接这两点进行折线逼近。该方法首先利用轮廓曲率角点检测算法检测出的两个相邻角点作为曲线的两个端点，然后根据折线逼近算法进行实验。算法的具体流程与折线逼近算法类似，结合轮廓曲率算法检测出的角点作为折线逼近的两个端点，再利用折线逼近算法进行规则化实验，实验结果如图5所示。可以看出，结合轮廓曲率角点的折线逼近的效果仍不理想，轮廓曲率角点检测算法在支撑区域较小的情况下，检测出来的角点不够齐全，会出现图中轮廓直角并非严格正交，如图中标注的虚线框部分。针对上述问题，本文制定了轮廓线规则化的基本原则，规则化的基本原则如下：

1）通过轮廓线检测得出角点坐标（x₁ ，y₁），（x₂ ，y₂），……（x_n ，y_n），每相邻两点可以确定一条直线，按照顺时针依次计算相邻直线段之间的夹角，夹角可由余弦计算公式求出。

2）判断计算出的直线夹角与90°的差值，设定15° 为夹角差值的阈值。如果计算出来的角度差值小于阈值，则进行直线正交化。将两直线段中较短的直线段强制正交于较长的直线段，使建筑物轮廓角严格直角化。若角度差值大于阈值，则不进行直线正交化，保留原状。

3）若计算出的直线夹角大于90°且与180°的差值小于设定的阈值，此处阈值也是15°，通过设定的阈值，可判断这两条之间的夹角接近于水平角，则将两直线段合并成一条直线。其他夹角的情况不进行任何处理。

4）若连续出现较多锯齿状，且直线段较短，直线之间的夹角接近于180°，则将锯齿状首尾的点连成直线。

通过上述方法对建筑物轮廓线进行规则化结果如图6（a），根据航拍影像图6（b）的判断，本文规则化结果符合实际情况。规则化的结果能够基本能将具有正交关系的建筑物轮廓线正交化。图6（c）是将规则化的建筑物轮廓线叠加到原始点云生成的深度影像上进行比较，从叠加效果图上可以看出本文算法基本能够得到较为满意的规则化结果。

4 结论

在角点检测全面且准确的情况下，基于轮廓曲率角点的折线逼近算法能够有效规则化建筑物轮廓线。如果角点检测不够全面，则需依据规则化原则对建筑物轮廓线进行规则化。本文的规则化原则在一定程度上能够满足建筑物轮廓线规则化的要求，但该算法没有考虑到弧线的规则化，算法还存在可改进的地方，值得进一步研究。