多边形面积计算教学的现状评析及优化途径

【摘要】多边形面积计算的教学不仅要让学生知道计算公式和求积计算，最主要的是通过图形面积的计算教学培养学生动手操作、主动探究的能力，发展学生的形象思维和空间想象力，从而培养学生的实践能力和创新精神。文章通过查阅资料，分析了多边形面积计算教学的理论现状，查找出教学过程中的一些问题，并给出了相应的教学建议。

【关键词】小学数学；多边形面积计算；现状；途径

【中图分类号】G623.5【文献标志码】A【文章编号】1004—0463（2022）14—0109—04

多边形面积的计算是空间与图形学习中的重要内容，通过割补、拼合等方法培养学生的实践动手操作、主动探究能力，发展学生的形象思维和空间想象能力，提升学生的推导能力。同时，多边形面积的计算是连接平面简单图形之间、平面图形与立体图形之间的关键内容，涉及平移、旋转等转化思想，为进一步学习空间立体图形的体积奠定坚实基础。小学五年级的学生初步具备了一定的平面几何基础知识，可以进行抽象思维，这个阶段正是培养学生几何意识，提升思维能力的关键时期。而如何利用多边形面积的计算教学提升学生的学习效率和学习质量，实现培养学生能力的目的是一线教师面临的一个课题，很多一线教师对此进行了很多有意义的思考与探索。下面，笔者就此问题也谈谈自己的看法。

一、多边形面积计算教学的现状评析

查阅知网，部分教师从小学生的年龄特点、认知水平、知识衔接点和教师的语言出发，设计出具有启发性、环环相扣的问题串，引领、驱动学生积极参与到三角形→平行四边形→长方形→梯形→五边形到其它多边形面积方法的推导过程之中，以期用最少的时间联系各类多边形的面积公式，从而达到提高课堂效率的目的[1]。浙江一位教师依据新课标要求，以具体的案例为抓手，强调了分割、平移、旋转、添补等方法在平行四边形和梯形面积计算方法推导过程中的运用，并通过从规则多边形到不规则多边形、单一多边形到多边形组合图形的面积计算方法的推导过程，达到学生对多边形面积计算方法的融会贯通[2]。也有一部分教师强调目标达成意识在多边形面积教和学中的重要性。简练的开场，先让学生明确学习目标，把一节课的总目标分解为具有从属关系和层级关系的小目标。在目标的引领下，展开学生的讨论和师生之间的对话，层层突破，逐层达成。通过不同多边形面积公式的推导过程和推导过程的多样性来提升学生对多边形面积计算方法的理解，既有严密的逻辑思辨过程，也有层层达成的推理过程[3]。总之，现有文献提出了很多有关多边形面积计算的教学思路，方法独特，观念新颖，但侧重点着眼于微观和具体的操作，而忽略了从整体和宏观上提炼把握。并且多数是在东部发达地区或城市学生的现状下进行的思考与探讨，对欠发达地区和乡村学生在视野上的受限性和发散思维上的不足考虑不周。因此，很多教和学的方法缺乏广泛的指导意义。想要让学生在多边形面积计算的学习中对教学知识融会贯通，必须要将教和学从重视多边形面积计算的基础上向促进学生空间观念发展及实际操作方面提升过渡。为此，笔者进行了针对性的思考，以期探索提高小学五年级多边形面积教学有效性的宏观性策略。

二、多边形面积计算教学过程中存在的问题

1.教师单元整合思维不足。单元整合强调把握单元内部各知识点具有共性的规律性特点和单元内部组成部分之间的联系理顺、理清，从而节省教学时间，提升学习效率，提高教学质量。在多边形面积计算的内容学习中，单元就是指在掌握平行四边形、三角形、梯形的面积计算的基础上对基本平面图形的组合图形面积的计算，以及不规则图形面积的估算，整个单元体现切割与组合的整体思想，单元整合教学要求教师将相互联系的内容结合起来，以实践操作引导学生完整理解知识。调查本地区多边形面积计算的教学现状，大部分教师忽略了知识之间的联系，按照教材的编排按顺序教学，将教与学的内容割裂成不同的小块，把重点放在了基本平面图形面积的计算上，而忽略了知识的整合，缺少整体规划意识，致使学生也难以从宏观上理解各知识点之间的联系，不利于整体思维的发展。

2.教师忽视了思维导图在学习中的作用。思维导图围绕一个核心关键词不断拓展延伸，将相关联的知识点以框架的形式紧密联系成关系图，简洁明了地展现单元内部知识之间的逻辑关系，引导学生快速吸收和消化知识，提高课堂效率[4]。然而，有一部分教师在教授完分散的各知识点后，就觉得这部分的内容结束了，并没有引导学生从整体的角度总结归纳这部分知识，尤其思维导图的使用少之又少。有一部分教师会给学生布置利用思维导图总结这部分知识的作业，但学生的整体思维发展不完善，接受的知识又比较零散，还不能独立地完成一份思维导图。缺乏教师的指导，学生的思维导图就没有系统性、不完整，学习效果大打折扣。

3.数学知识与生活脱节。瑞士心理学家皮亚杰提出“认知基模”的概念，认为人的大脑中存在一种基模，可以将不同的知识连结，并且将新的知识准确归位于一个大的概念之中。因此，在教学中，数学教师应时刻渗透数学生活化意识，不断塑造和完善学生的数学“认知基模”，让学生能够接触到一个数学概念之后条件反射出相关的大概念。而在多边形面积计算的教学过程中，多数数学教师依然采用传统教学模式，以公式的应用与积的运算为主训练学生的计算能力，忽视了学生的生活经验，使得在解决一些组合图形和不规则图形面积的组合与分割时，学生遇到了障碍，不能灵活应用基本图形进行组合图形与不规则图形的面积计算，难以获得理想的教学效果。

4.教学模式陈旧。随着新课改的深入推进和信息技术的普遍应用，很多教师把一些教学软件、网络资源应用在自己的课堂教学中，但教学模式却是“换汤不换药”，教师展示操作过程，学生跟着教师的思路被动接受知识，亲身操作体验的机会很少。尤其在多边形面积计算的学习中，有许多图形的面积要通过折叠、裁剪等方式组合与切割才能求解，需要学生实践操作认识图形之间的联系，从而获得真实的体验感受。若教师采用多媒体演示讲解，会让学生失去自主探索的兴趣，得不到更佳的学习效果。

三、多边形面积计算教学的建议

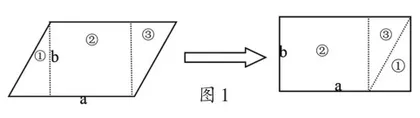
1.强化单元整体教学。单元教学设计就是设计者从一章或是一个单元的角度出发，根据章节或单元中不同的知识点的需要，综合利用各种教学形式和教学策略，通过一个阶段的学习让学习者完成对一个相对完整的知识单元的学习。在多边形面积计算的教学中，教师有意识地联系本单元中涉及的知识内容，根据学生的个体差异和知识掌握程度重新构建知识框架，引导学生自主学习，不断开发学生的智力，提高其学习效率。多边形面积教学教材的编排顺序是从单一平面图形到组合图形，在单元整合教学模式下，可以专设一课时，通过切割、平移、旋转等方法理清单一平面图形之间、单一平面图形与组合图形之间的关系，然后依据已学知识解决相关问题。例如，平行四边形面积计算方法的推导，可以将三角形和正方形面积的计算整合起来，如图1，求平行四边形的面积可以通过剪拼拼接成长方形，利用长方形的面积计算方法求解。这样，解决了平行四边形面积的推导，又将三角形、正方形、平行四边形等多边形单元知识跨课时整合在一起，既展现了单元知识内在的联系，又训练了学生的发散思维和推导能力，让学生能够获得对多边形面积的更深刻认知。这尊重了学生的个体差异，开发了学生的智力，提高了学习效率。

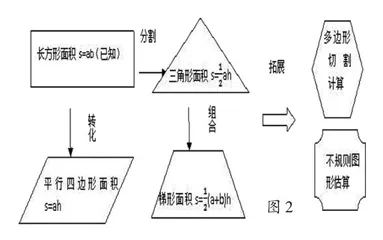
2.巧用思维导图。思维导图能把多边形面积中涉及的各知识点的相互隶属关系与相关的层级表现出来。课堂中利用思维导图归纳总结知识之间的联系，学生就可以把握知识之间的内部联系，灵活应用基本平面图形解决组合图形与不规则图形的面积计算，提高课堂学习效率。为此，教师应该在备课过程中就构建出系统的导图框架，将一整节课堂变成一个思维导图的展开和拓展过程，让学生跟随自己一起完成思维导图。例如，上课一开始，教师就设定关键词，引导学生按照课本上的知识内容拓展延伸，学生根据教师的讲解和自己对知识的理解程度不断补充完善，最后形成学生自己的知识体系图，不但掌握了知识点、方法，还有利于学生形成严谨探究的良好学习习惯，为学生的终身学习打下基础。此外，教师可以拆解不同关键词，让学生组合成小组，合作完成对某一知识点的探究，并完成与该关键词相关知识的思维导图，直到填充完成一整节课的思维导图。比如，多边形面积的计算在确定分割、转化、组合等关键词的基础之上，可以生成如下思维导图，如图2。这样可以通过思维导图有效提升课堂的互动性和趣味性，从而提升学生对于多边形面积这一章节的兴趣。

3.融通生活，培育素养。新课标对课程教学提出了更高的要求，教学目标也不仅仅局限于使学生获得数学技能与数学知识，更重要的是用数学的思想和方法解决生活实际中遇到的问题，达到培育、提高学生学科素养的目的[5]。源于生活经验的教学效率更高，学生能动性更强，更有利于学科素养的提升。因此，教师在多边形面积计算的课堂教学时，应搜集更多基于生活方面的知识，依靠学生身边的素材，将课堂知识与学生生活身边的事物联系，让学生对抽象知识有更清晰的了解，也能够让学生更好地理解多边形面积的计算。例如，“多边形面积的计算”教学中，在完成课堂基础知识教学的基础上，可以组织学生开展校园相关区域面积计算的探索活动，让学生更深刻理解数学与生活之间的内在联系。数学是生活现象的抽象概括，又可被具体化应用于生活中。小学生正处于思维开拓的关键时期，对生活也有热情与好奇心，正是培养学生几何思维的关键时期。因此，在多边形面积教学中融入生活经验，能够让学生更好地理解多边形面积的计算，掌握多边形面积的计算技巧。同时，学生认识到数学知识与实际生活的关系，将学到的数学知识应用到生活中解决实际问题，进而能够达成解决问题中形成技能的目的。

4.改变课堂教学模式。改变课堂教学模式，意味着教师不再完全是课堂的管理者，而逐渐成为学生学习过程中的引导者和学习活动的参与者。教师可以因材施教，保证学生的个性得到充分展示，让学生逐渐建立起自主探究与学习的良好习惯，真正从传统的被动接受知识的角色转为主动的知识探索者，从而达到提高课堂学习质量，提升学科素养的目的。在进行平行四边形面积教学时，教师可以让学生准备长方形、平行四边形纸片各一个，先让学生讨论、发现二者的联系与区别，而后利用割补、旋转的思想进行平行四边形和长方形之间的转换，最后在已知长方形面积计算方法的基础上推导出平行四边形面积的计算方法。这样，在割补的过程中，学生的能动性被充分调动起来，教师再辅助指导，学生的积极性会更高。而学生在割补的过程中因为操作的差异，割补后形成的长方形可能不规则，教师可以引导学生讨论产生问题的原因及解决措施。突破了平行四边形与长方形的转化，平行四边形面积公式的推导就顺其自然的完成了。这样，教师在实际教学中灵活转换教学模式，以便体现学生在课堂教学中的主体地位，重视课堂提问、课堂情境设置等教学环境，采取一定的教学辅助手段，创设丰富而多样化的课堂教学氛围，让师生之间的互动更为多样化，激发学生的主观能动性和求知欲，让学生在探索中主动作为，既有利于学生对多边形面积计算方法的灵活运用，又能增强学生的团队协作意识，提高动手能力。

综上所述，教师要提高多边形面积教学的有效性，不但要强调计算方法等教学细节和微观操作，还要从宏观上进行单元知识的分析与整合，注重思维导图在多边形面积教学中的应用，让学生理解并掌握单元知识内在的逻辑关系，学生切实让理清思路，把控知识之间的区别与联系，从而对多边形面积的计算应用达到融会贯通，灵活运用，提高学习效率，培养推导能力，达到培养、提升学生学科素养的目的。

参考文献

[1]沈雪艳.基于启发性提示语的教学设计探索——以多边形面积公式为例[J].数学之友，2021（03）：53-54.

[2]罗世土.转换思维巧分割——“多边形的面积”案例分析与探讨[J].数学教学通讯，2014（10）：09-10.

[3]王海峰.聚焦增值，让数学复习课温故知新——以苏教版五上《多边形面积计算的复习》的教学为例[J].江苏教育，2020（89）：58-61.

[4]杨红波，江保成.把握单元教学特点促进课堂教学高效——“多边形的面积”单元整体教学的实践与研究[J].湖北教育（教育教学），2013（10）：17-18.

[5]任加顺，顾美华.抓住核心问题提升思维价值——“‘多边形的面积’整理与复习”教学片段[J].小学教学：数学版，2019（12）：57-58.

编辑：徐春霞