借“微整复习” 让图形思维生长

摘 要 《义务教育数学课程标准（2022年版）》（下称“新课标”）对于如何上好数学复习课给了很好的启示：整合和结构。通过将关联知识进行整合设计，结构形成进阶式的立体支架，让学生的思维在“攀爬”支架的过程中生长与繁茂。通过点、线、面、体不断变形与深入，学生在资源的更新迭代中形成问题链，激起迫切解决问题的思维波澜；在对图形多次感性观察丰盈后，进而抵达立体图形计数、升与毫升量的计量的整体抽象。

关键词 图形复习 整体性 图形思维 增值评价

《义务教育数学课程标准（2022年版）》提出了“整合”理念，围绕“三会”培养目标将图形知识进行微整合，将“平面上两条直线的位置关系”“角的知识”“观察物体”“复杂形体”和“升和毫升”相关知识进行跨单元和跨域有效串接、多元融合，让微课“微”而不“小”，“微”而不“浅”，使学生在微整的复习氛围和多元的数学表达中激发出更多的思维火花。围绕发展性，在数学观察能力、数学表达能力上多施“笔墨”，能促进学生评价的“自我增值”。笔者将苏教版数学四年级上册期末复习的“图形王国”进行创新式开发，以兼容线上与线下教学整体支架的结构呈现，同时还可以生长成普通的线下教学，形成资源的“跨线”增值。

一、连点成线，形成“微整”意识

此环节将成为本复习课的引子，通过对点的延伸形成射线和直线，再利用点整构成线段、射线和直线的融合体，引发学生对图形继续联想的驱动力。

师：瞧，这里有一个点，它向右边不断延伸，变成了什么？

生：变成了一条射线。

师：是的。从这个点又向相反方向延伸，这时变又成了什么？

生：成了一条直线。

师：老师在直线上又点了两个点，想想现在有多少条线段？有多少条射线呢？先暂停，数一数。

生：有3条线段，6条射线。

【思想路径】回溯上述的教与学，笔者让学生重点回顾了射线、直线和线段，从特征感悟和量的规律寻找上，进行练习和简要回忆性复习，图形知识生成自然有序，在微整合的过程中让学生感受到资源不断生成的“神秘”推力。

二、旋线定位，蕴含随机理念

这部分教学，要从线的平移特别是旋转中创造出新的随机资源，通过暂停运动的线条，进而生成两线关系的静态资源——平行（不相交）与相交，再在线组关系的识别和分组中自然地促进两线关系的深度复习。

师：刚才我们由点产生了一条直线。瞧，又一条直线落下了，两条直线在同一平面，你发现每组直线存在什么关系？

生：是互相平行。

师：瞧，现在老师让一条直线旋转起来，如果点屏幕暂停，你将看到这两条直线是什么关系呢？同学们先观察一下线的旋转，再点屏幕暂停。

师：你的暂停点好了吗？老师点了暂停，你的两条直线关系是不是和我的不太一样？

生：是的。

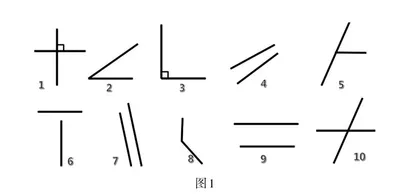
师：这里，老师也截取了10位同学暂停后的图形（如下图1）。你能说说哪些组的两条直线是相交的，哪些是不相交的？同学们点屏幕暂停播放进行思考。

生：我认为7号和9号是平行，也就是不相交，其余都是相交。

师：4号6号为什么是相交呢？

生：只要延长线就可以相交了。

师：老师来延长一下这两组中的线。咦，它们真的相交了！看来，不能被它们表面现象迷惑。

师：结合同学们的图形，老师整理一下同一平面内两条直线的关系，这个大圈被分成两部分，分别表示什么呢？（如下图2）

生：分别表示平行（也就是不相交）和相交关系。

师：这里又出现了一个小圈，表示什么呢？

生：表示这两条直线互相垂直。

师：下面请大家暂停屏幕，将右边10组直线的关系分别填进圈中。互相平行有哪几组线呢？

学生独立思考，自我回答。

师：对的，第7组和第9组线，两条线都是互相平行。互相垂直是哪几组？

生：1、3、6组。

师：这位同学说是1、3、6组，填得很正确！剩下来的都应该是相交，看填在这个位置（指向中间位置）。

生：老师，我觉得垂直也是相交，所以相交的有第2、4、5、8、10和1、3、6组线。

师：你很爱从不同角度思考，而且更值得点赞的是，你还学会用恰当的词语来组织表达，例如，我觉得……，因为……所以……

【思想路径】上述教学利用了线条资源中的动、静结合，让学生在感受自己创造资源的快乐中，也激发出他们问题发现及解决意识，促进积极情绪体验的生成；在线组分类中，采用集合图和严谨的数学结构语言相融合，促进学生用数学的语言进行多元表征。

三、辨角妙施，“述算”创生模型

此段的教学环节将围绕角展开，从线组的资源里择取角并进行思维“聚焦”，先要对角进行分类回忆，再进行角的大小计算，需要重视对学生计算思维表述能力（述算）的培养。

师：同学们很爱思考。两条直线相交后会产生很多角，我从同学们的作品中就选取了三个角，分别是第2、3和8组线（如图3），回想一下，这些角分别是什么角？

生：从左边起，第一个是锐角、第二个是直角、第三个是钝角。

师：我们学习过的角就这几种吗？

生：不是的，还有平角、周角。

师：这些角分别有什么特征？

生：锐角大于0°而小于90°，直角等于90°，钝角大于90°而小于180°，平角等于180°，周角等于360°。（如图3）平时用的三角尺上就有一个直角两个锐角。

师：其实，两条直线相交后有很多个角的。瞧，你能分别算出∠2、∠3、∠4的度数吗？请点屏幕暂停，自己做一做（如图4）。

学生独立完成。

生：我们只要用平角减一个角就可以求出相邻的另一个角。

师：是的，你做对了吗？

师：这两根直线像这样相交，你又发现什么秘密？

生：我发现“对面”（相对）的角度数相等，∠1和∠3度数相等，∠2和∠4度数相等。

师：真棒！看，这里有好几条直线相交了，条件是这样的，你觉得∠4该怎么求？（如图5）点屏幕暂停，想一想，动笔算一算。

生1：我用平角减去∠2和左边的直角，就可以求出∠4 = 180°－32°－90° = 58°。

生2：∠1和∠2的和是直角，我们还可以用∠1 = 90°－32° = 58°。由于∠1和∠4是两条直线交叉后“对面”（相对）的角，所以，∠1 = ∠4 = 58°。我觉得这种方法更简洁，∠3的度数在这里不用。

师：两位同学回答得很好，特别是有自己不同的观点时能大胆表达，值得表扬。

【思想路径】以上安排的教学，利用前面截屏的10组两线关系图，选取其中3个角，自然地形成并完善了角的分类及特征的整理和复习；在角的计算中，笔者先抓住“对面的角”（相对的角、对顶角）的特点，让学生感受线和角蕴藏的规律，进行小学和初中长线衔接；之后角的计算问题，让学生对比探究：用发现的规律有时可以快速判断出角的度数。

角的度数计算环节，使学生从更广的视野观察角，用刚才更新的思维来计算角：学生学会了对比、整合，灵活运用角的知识解决问题。值得关注的是，此处教学十分重视计算与图形的贴合，“述算”和“述图”的结合，创新观察和创新思维的融合。

四、围面成体，空间想象进阶

以下教学，先要将“线组”升级成“群组线条”；学生通过画多组纵横等距离平行线，发现面的“群体”存在；再通过涂色凸显部分面，利用剪切、折围，运用操作和空间想象把线、面向体转化。

师：照样子画一画几条互相平行的横线，相邻两条平行线之间距离都是1厘米。你发现多条平行线之间是什么关系？

生：我发现他们都互相平行。

师：在横的平行线组上再画几条垂直的平行线，并调整到相邻两根平行线之间的距离都是1厘米。那么，横竖线之间你有什么发现？

生1：我发现，竖线之间都互相平行，它们和横线都互相垂直。

生2：我还发现交叉形成了方格图。

教师出示方格图。（如下图6）

师：请点屏幕暂停，在自己画的方格图上，照样子涂出6块方格颜色。学生涂色操作。

师：这是一个神奇的图形，我现在把它剪下来，瞧，折叠并围一下就可以变成什么？

教师用动画演示把图形折、围变成一个正方体。（如上图7）

生：成了一个正方体了，我也想试一下……

师：嗯，你们可以暂停播放尝试一下哟！你会有更多发现的，是不是也能带来一些思考呢？

生：我想到了平时堆作业本的情况，发现了如果用很多同样的正方形的纸也可以堆出正方体。

师：当正方形有了厚度就慢慢“长成”了正方体，就像学习知识，除了知识面变广，还要对知识有一定深度的了解，这样才是真学习。

【思想路径】此环节通过横向和纵向等距平行线组的垂直绘制，画出众多方格，让正方体展开图有了生长背景；然后顺水推舟，进行组合图形（正方体展开图）的涂、剪和折。从线到面，这时又过渡到正方体，发展不着痕迹，体现图形知识之间的密切联系，学生的形象思维、抽象思维及创造性思维，在教师的增值引导、鼓励和评价中进一步整合。

五、窥体促思，多维观察融通

此处教学，先要将多个正方体进行拼搭形成组合体，从观察一个组合体多个面，然后引导观察多个组合体的多个面，在三维和二维的关联碰撞中，整合多维空间发现。

师：老师课前收集了一些同学折、围、粘好的这样相同的小正方体，我们可以搭建出各种各样的立体图形。瞧，这里就有三位同学用5个小立方体搭成的形体，请将观察到的形状和方向连一连。先点屏幕暂停。

学生操作连线。

师：好了，是不是这样？（如图8）

师：你们真厉害！有同学用4个相同的小正方体组成了下面的三组组合体，如果从同一个方向观察，你看到的是否相同？（如图9）点屏幕暂停想一想、画一画。

生：我发现上面看都是横着的三个正方形，都相同；还发现从前面看第一个是L型、第二个是倒“T”字型、右边是左右相反的L型；从右边看都是竖着的两个正方形，是相同的。

师：哪个或哪几个组合体，前面和后面看到的平面图形是一样的？（如图9）

生：第二个组合体前、后看到的平面都是倒“T”字形，其余两个组合体看到的是前、后相反的。

师：有没有哪些组合体不同面看到的是相同的？

生：第一个组合体的前面和第三个组合体后面看到是一样的……

【思想路径】前面的教学是从点、线、面、体逐步深入的，这里的教学是体、面交融，从正方体的不同搭配对比和视角的转换中寻找平面，学生的观察和想象在三维和二维中变换。这部分教学内容相对比较抽象，需要较强的空间想象力，因此，笔者在这里重点进行了三重进阶对比训练：一是“一体多面”，即通过一个组合体进行多面观察，唤醒学生的观察方法；二是“多体同面”，即通过三组组合体进行同方向观察，发现面的相同和不同（正方体数量相同、观察角度相同，观察结果有可能相同也可能不同）；三是“多体多面”，即多组组合体自我不同面之间对比，不同组合体不同面之间进行对比。此环节的思维挖掘空间是具有弹性的，灵活的评价也能促成自我增值与个体成长的拔节。

六、组面构体，逆向思维建构

在丰富面、体的学习感悟后，这个环节，学生将观察到的不同面进行关联并且联想出组合体。教学将再次引导学生从面的不同属性和形状中，进行操作、联想和体的复原。实施教学中，需要对图形计数和空间思维的语言表述能力培养加以关注。