“以问促学”，提升学生解题的能力

【摘要】在小学数学教学的过程中，教师不仅要让学生理解数学的基础知识，还要引导学生运用这些知识对问题进行具体分析、精辟理解和独立解决。教师可借助“以问促学”的方式，巧设问题，激活学生的思维，引导学生探索解题思路和方法，促使他们以灵活而又富有创造性地解决问题，从而提升他们的解题能力。

【关键词】小学数学；“以问促学”；设置问题；解题能力

作者简介：周莹（1997—），女，江苏省南通市海安市城东镇韩洋小学。

在当前“双减”政策的背景下，教师一方面要提升学生的解题能力，提升学生的数学素养；另一方面又要切实减轻学生的负担，减少作业量。基于此，教师可通过“问”的方式，让学生主动参与解决问题的过程中，提升学生解决问题的效果。具体而言，教师要借助问题，拓宽学生的思维视野，引导他们思考解题思路和方法。以苏教版小学数学五年级下册“圆”的教学为例，教师从“问”出发，为学生解决问题找寻突破口。

一、在自学中合理设置问题

教师应为学生提供充足的学习时间，引导学生自主学习，让自己探索解题的路径，增强学习体验，从而提升解题能力。基于此，教师可在预习环节中设置一些问题，让学生在问题中学习，在学习中提升［1］。

在“圆”的教学过程中，教师可以先将该章节的标题呈现在黑板上，让学生阅读这些标题，使他们对即将学习的内容有初步认识。这些标题为“圆的认识”“扇形的认识”“圆的周长”“圆的面积”等。教师可围绕这些标题设置一些问题，让学生借着问题自主阅读教材的内容。这种让学生以单元为主的自学，能让学生整体感知知识，培养他们的全局思维。其中，教师设置的问题为：“你在生活中见过哪些与圆相关的物体，这些物体有什么特点？”“由扇形，你首先想到什么物体，你认为它跟圆有什么关系？”“周长的定义是什么，我们学过哪些图形的周长？”“我们学过哪些图形的面积，面积的概念是什么？”“你能想象出与圆组合的图形都有哪些样子？”教师设置的问题能明确学生的学习方向，让他们集中思维，进而提升自学的效果。具体而言，学生会从教材中寻找具体的方法，当暂时找不到答案时，他们会继续探索，从而促进他们的深度思考。此外，教师在设置自学问题时，要注重问题的合理性。第一，教师提出的问题要有一定的体系，问题之间要具有连贯性，能启发学生展开联想。第二，教师设置的问题要让学生联系自己的学习经验，同时又要能引导他们借助已有的认知进行拓展，促成新问题的解决。第三，教师设置的问题要联系学生的生活与情感，要能让他们自然而然地进入思考的情境，这对解决问题大有裨益。

可见，教师将“以问促学”作为一种教学策略，指导学生自主学习数学知识，通过提出问题激活学生的思维和学习动力，从而让学生在自学的过程中提升学习能力和解题能力。此外，教师设置问题时，要注重合理性。合理的问题能够更好地激发学生的思维，促使他们深入思考、提出假设，进而加深对知识的理解和应用。

二、在导学中分层设置提问

在导学时，教师应引导学生发挥主观能动性，让学生保持较好的学习状态。具体而言，教师应设置一些问题，推动学生思考，促进他们自主解决问题。然而，学生的解题能力是有差异的，教师应基于学生的解题能力，设置有梯度的问题，让不同解题能力的学生都能解决他们能力范围内的问题。教师分层设置问题，能够更充分地调动学生的积极性［2］。

在“圆”的教学过程中，教师展示以下情境：将一个直径是4分米的圆等分成若干份剪开，再拼成一个近似的长方形。首先，教师设置理解性问题：“这个情境与所学的哪些数学内容有关？”“能不能将题目中的关键词划出来，再说出它们的定义来？”“能不能将这个情境中的已知条件列出来？”“能不能用自己的话把这个情境重新说一遍？”这些问题能逐渐引导学生准确理解情境，有利于提升他们的解决基础性问题的能力。接着，教师设置一些分析性问题：“将一个直径是4分米的圆等分成2份，你会怎么做，那么4份、8份呢？”“这个情境中涉及哪些数学概念和原理？”“如果将圆等分后，每一份又是什么形状？”“你认为剪成多少份之后，才能够拼成近似长方形的图形？”这些问题能够促使学生运用数学知识进行分析和推理。而后，教师设置探究性的问题：“如何确定拼成的长方形的尺寸和面积？需要关注哪些因素？”“能否尝试将圆等分成若干份，再拼成近似长方形？这样的操作对拼接结果有什么影响？”这些问题需要学生思考不同的因素，并进行试验和比较，从而使问题得到解决。

教师分层设置问题能够满足学生的个性化学习需求，让他们能在自己的能力范围内参与解决问题的过程，进而提升解题能力。

三、在互学中设合作性问题

互学即学生相互学习。在数学教学的过程中教师应设置互学环节，让学生汲取别人的智慧，解决自己的问题，从而促进学生综合素养的发展。具体而言，教师可巧设一些合作性的问题，从而培养学生的合作能力，增强学生的解题信心。

在“圆”的教学中，教师设置以下问题：“从一张长7.8分米，宽2分米的长方形纸上剪出一个最大的圆，这样的圆最多可以剪出多少个？”首先，教师将学生分成不同的小组，指导学生动手操作按照问题要求剪出多个的圆形。在此过程中，学生需要独立地完成“剪”的任务，他们可多次尝试直到剪出他们认为最佳的答案。接着，教师引导学生分享“剪”的过程中的感受。有学生认为最大的圆要能在纸上找出最大的半径，这个最大的半径应该是7.8分米；也有学生认为这个圆的直径其实就是长方形的宽。对于不同小组的结论，教师要给予正面的评价，对学生积极思考的表现进行肯定与鼓励。教师可引导学生对这些问题再思考，鼓励学生提出自己的新观点。此外，教师在设置问题时，要考虑学生的合作潜力，引导他们在彼此的帮助下进行多角度的思考。

可见，教师将提问与合作结合起来能让学生更好地讨论和深入地思考，使他们更容易从问题中提取关键信息，从而开展相关的学习活动。值得注意的是，教师要引导学生学会倾听他人的观点，同时要能表达自己的观点，从而提高学生互学的效果，促进问题的解决。

四、在探学中相互质疑

探学环节即教师为学生提供充分的互动与探究的机会，促使学生积极展示自己的思维成果；相互质疑则强调学生之间的互动和对彼此观点的质疑和辩论。在探学中，教师可引导学生相互质疑，让他们自己开展“以问促学”，相互提出问题，同时围绕问题进行辩论。这种方式能让学生之间产生更多的“问”—这个问是民主的、平等的，学生可以自由地问别人，可以被同学自由地问。在此过程中，每次产生的问题都能得到及时的反馈，能够对问题的解决提供更多的可能性。值得注意的是，学生需要甄别其他同学的回答，这有利于培养学生的批判性思维和分析问题的

能力。

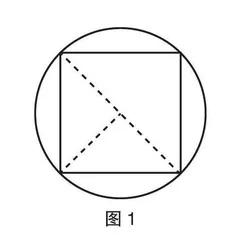
具体而言，为了引导学生相互质疑，教师为学生提供探究性问题：“以图1为例，正方形的面积是10平方厘米，圆的面积是多少？”

首先，教师让学生互相展示解题过程，然后让他们就不同的答案进行质疑。其中，一名学生给出的答案为：圆的面积＝πr²=π102（平方厘米），而其他学生质疑道：“能确保圆的半径是10厘米吗？”另一学生给出这样的答案：圆的面积＝πr²=π52（平方厘米），而其他学生质疑道：“能确保圆的半径是5厘米吗？”有学生独辟蹊径给出这样的思考：如图1所示，将正方形分成两个三角形，其中一个三角形的面积是5平方厘米；这个面积是2r乘以r再除2的结果，因此就可得出：三角形的面积＝底×高÷2＝2r×r÷2＝5（平方厘米），据此可得r2＝5。这时，还有学生提出疑问：“求出半径的平方作用是什么？求圆的面积需要的是半径。”其他学生补充道：“不需要求出半径是多少，将半径的平方代入圆的面积的公式就可以了。”在彼此质疑、相互补充的过程中，问题逐渐得到了解决。

可见，在数学教学的过程中，教师应设置多样化的活动，让学生在具体情境中主动、互相地提问，鼓励学生对别人的观点与见解提出疑问。如此，能够让学生从不同的角度看待问题，拓宽学生的视野，让他们在共同努力、相互帮助下有效地解决问题。

五、在延学中自主设置问题

延学主要是指学生在课后所开展的学习活动，其是课堂的延续，能够帮助学生巩固所学的内容，促进学生思维的进一步发展。一般来说，教师可以通过自主学习、课外辅导、兴趣俱乐部等形式呈现延学。在开展延学时，教师可呈现相关的话题，让学生自主设置问题，开展自主探究。教师关注的不只是学生探究的结果，而是他们提出多少问题，这些问题的质量如何，以及他们探究的过程。就“以问促学”而言，让学生不断地问是学生提升能力的关键。

在延学过程中，教师设置这样的话题：“珊珊将一个圆平均分成若干等份后，拼成一个近似的长方形，其周长增加了4分米。”学生可根据话题进行动手操作，再提出不同的问题，也可围绕情境的每个环节提出疑问，还可提出由这个情境可能得出的一些结论。学生提出的第一个问题是：“珊珊将圆平均分成多少等份，才能将这些等份的圆块拼成一个长方形？”学生之所以提出这样的问题，是因为他们发现如果分成的等分比较少，是不能拼成长方形的。学生提出的第二个问题是：将圆平均分成若干等份后，再拼成长方形的过程中，原来圆的面积有没有改变？学生之所以提出这样的问题，是因为他们在操作的过程中发现圆的面积发生了变化。接着，学生又提出这些问题：“拼成的长方形的特征和性质有哪些，长方形的长、宽比是固定的吗？”“周长增加4分米，这是如何计算的？”此外，教师可通过提示引导学生寻找关键词，让学生围绕这些关键词提出新问题。基于教师的提示，学生提出问题：“原来圆的面积是多少平方分米？”对于这样的问题，部分学生仍存在疑惑。教师可再次提醒学生要从关键的信息进行突破。于是有学生提出这样的问题：“把一个圆平均分成若干份后，拼成一个近似长方形，周长增加了4分米意味着什么，能不能找出可以转化的信息？”学生在操作中发现拼成的长方形的周长其实比原来圆的周长增加了2条半径的长度。有了这样的发现，学生列出式子：3.14×（4÷2）2＝12.56（平方分米）。在延学的过程中，教师鼓励学生不停提问，使他们有了不停解决问题的机会，因此数学能力真真切切地得到了提升［3］。

“以问促学”的根本目的是让学生“学起来”，发展学生的综合能力。教师在设置“问”的时候，应为学生提供充足的自主空间，给予学生自主选择感兴趣的问题并进行探究的机会，激发他们“问”的热情，提高他们主动解决问题的积极性，从而培养他们的综合素养。此外，在自主设置问题时，学生需要进行信息的收集和整理，以及对问题的筛选和评估，如此有利于提升他们的数学学科能力。

结语

“以问促学”借助“问”，拨动学生的思维的“弦”，促使学生深入理解和思考所学内容。基于这样的理解与思考，当学生遇到新的问题之后，他们能够明确自己在问题中的疑惑点，尝试不同的方法和角度，独立探究和实践，从而运用自己的知识进行探究和解决，并从中领悟更多的解题路径。

【参考文献】

［1］陈仁建.以问促学的小学数学教学策略［J］.学园，2024，17（6）：43-45.

［2］贺慧，王素月.中小学作业的本质厘清、问题审视及形态再构：以北师大版五年级数学作业设计为例［J］.北京教育学院学报，2024，38（1）：56-64.

［3］陈敏.以问促学 以疑导学：问题导学策略在小学数学教学中的运用［J］.学苑教育，2023（3）：29-31.