在中学数学教学中融入数学建模思想的研究

摘 要：数学建模思想融入到中学数学教学中，对于提升素质教育，培养学生的创新能力、创新思想、学以致用等方面具有重要的意义。为此，针对数学建模的各环节，教师分别采取的引导方式成为数学建模思想融入到教学实践的重要内容。

关键词：数学教学； 数学建模； 教学改革

中图分类号：G633.6 文献标识码：A 文章编号：1006-3315（2015）01-022-001

中学数学教育新课程标准和数学教育改革以及教材的编写都要求以“数学素质教育”为目标，突出了理论与实践相结合，更加注重学生对数学知识的应用，强调学生数学应用意识的培养。在新的课程标准中明确指出：“在原分析和解决问题能力的基础上，进一步提出培养学生发现和提出问题的能力”、“在教学中，应注重让学生在现实背景中理解基本的数量关系和变化规律，注重使学生从实际问题中建立数学模型、估计、求解、验证解的正确性与合理性的过程[1]”等。这都要求数学建模思想要融入中学教学之中去，这也是素质教育和学以致用的行之有效的策略。

1.在中学数学的教学中融入数学建模思想的策略方法

1.1数学建模的基本构建环节

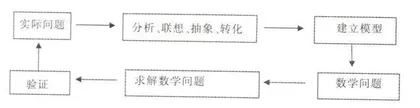
在中学数学的教学中融入数学建模思想，首先要搞清数学建模的基本构建环节，数学建模是运用所学知识求解实际问题的过程，这需要对实际问题简化、抽象、概括、归纳等，并运用数学的语言建立数学模型，求解，最终返回到实际问题，从而解决实际问题。中学数学教学中，要使学生初步学会建立数学模型，提高学生应用数学求解实际问题的能力，大致可按如环节进行（如图1）：

1.1.1问题的分析。对于建模问题，由于实际问题的题目一般涉及名词、述语较多，内容也较多，因此要认真审题，分析实际问题的背景，探索问题的内在规律，弄清问题的已知和求解是什么。

1.1.2对数据、资料的收集和整理。搜集信息资料也是建模的一项重要工作。对于实际问题的理解和分析中，一般需要查阅相关的数据、资料，从而形成对问题更加清晰的认识，搜集和整理资料往往要用到数据库和检索工具，在确定数据有效性的基础上对其分析、整理。

1.1.3对实际问题合理假设和简化。根据实际问题的特点和建模的目的，对问题进行必要的假设和简化，才能适合数学研究的要求，同时对问题的本质也能理解更深。

1.1.4建立模型。一般来说，数学模型可以描述为对于现实世界的一个特定对象，为了一个特定目的，根据特有的内在规律，做出一些必要的简化假设，运用适当的数学工具，得到的一个数学结构[2]。经过对实际问题的简化之后，通过分析、联想、抽象等过程，对问题用数学的语言来描述，从而将问题转化为数学模型，这要求学生不但有一定的抽象能力，而且还要有观察、分析、类比、综合等能力。

1.1.5求解模型。运用所学数学知识，对模型求解。这正是学生运用所学数学知识求解的过程。对这一过程学生并不陌生，但可能运用的知识并不熟悉，这也要求学生主动地查阅文献资料，寻求求解方法。学生的学习也由平时的被动学习，变为更培养能力的问题趋动的主动学习、研究性学习，这将极大地激发学习数学的热忱。

1.1.6将结果返回实际问题检验。模型求解之后，将解返回到实际问题论证分析，检验结果的合理性，能否给出实际问题的解答，如有偏差，问题出在哪里，从而修改模型，再进行求解和检验。

2.教师在中学数学的教学中融入数学建模思想中的引导

在中学数学的教学中融入数学建模思想中，学生是主体，教师是主导，教师的引导是关键。教师应在建模的不同环节，适时地给予不同的引导。在这些环节中，教师的引导对于培养学生的创新意识、创新能力、沟通能力、团队协作精神等方面意义重大，而这些能力的培养要贯穿于教学的一点一滴。

2.1在问题分析阶段的引导

在此阶段，学生对于问题的认识还比较粗浅，甚至一些名词、术语还不是很清楚真正含义，这时教师有意识地应引导学生到图书馆查阅相关书籍、电子文献等。在此基础上，教师还要引导学生洞察问题的内在联系，探究问题的内在规律。

2.2在数据、资料的收集和整理阶段的引导

在此阶段，教师要鼓励学生查阅相关文献，以网络、调查问卷、甚至是自己动手做实验等方式采集数据，并对数据、资料进行整理加工，剔除与问题无关的内容，对重要信息要做好记录。

2.3问题的假设与简化阶段对学生的引导

在此阶段，教师要引导学生注意假设的合理性与简化程度的适当。要保留影响问题结论的主要部分，取舍得当。

2.4建立模型阶段的引导

有了之前充分的准备，此阶段要充分发挥学生的主观能动性，鼓励学生认真分析思考，探索问题的内在演化规律，并用数学的方式描述清楚，从而建立出数学模型。

2.5模型求解阶段的引导

在此阶段，充分发挥学生的主观能动性，但在学生确实有求解上的困难不易解决的时候，教师可以引领学生进行相关知识的学习，或帮助查阅文献来解决。

2.6模型的解的检验

模型得解之后，返回实际问题进行检验。利用实际问题检验模型的解是否能解决问题，误差是多少，能否改进，以及假设简化的合理性等等，并给出改进方案。

总之，在教师的引导下，要注意发挥学生的主观能动性，对于学生观点的合理性和可取点要充分肯定，对于明显不正确的思路和方案，也要给学生时间去思考有没有改进方法，尽量以学生为主体，让学生按他们自己的想法和思路完成。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准解读[M]北京：北京师范大学出版社，2011

[2]姜启源，谢金星，叶俊.数学模型[M]北京：高等教育出版社：3-4

[3]中共中央关于全面深化改革若干重大问题的决定[N]新华每日电讯，2013年11月16日