适应个性 巧设练习 促进发展

摘要：学生个体发展存在一定的差异，我们在设计练习时，要注意适应学生的个性，巧妙设计数学练习，促进不同学生的发展。

关键词：个性；练习设计；发展

中图分类号：G623.5　文献标识码：A　文章编号：1006-3315(2010)8-101-001

《小学数学课程标准》明确提出：“不同的人学习不同的数学，不同的人在数学上得到不同的发展。”小学数学教学中，老师常常规定同学们在同样的时间内完成同样数量、同等难度、同样内容的作业，一部分学生很快完成了，而另一部分学生却迟迟无法完成，造成“学困生吃不了，学优生吃不饱”。因此，我们在设计数学练习时，要注意适应学生的个性，注意层次性，促进不同学生的发展。

一、“套餐型”练习

我们应以学生为本，改变传统的“千人一面”的做法，为不同层次的学生设计不同的练习，即“套餐型”练习，这样才能真正满足不同学生的需求。我们可以把练习设计成三种不同的套餐。套餐A为简单的巩固性练习；套餐B为较高一层次，带有一定的拓展性；套餐C的要求更灵活多样，偏重于理解、想象、运用。学生可以根据自己的能力和需要，选择其中的一套或几套完成。

如学习了圆柱的体积后，我们可以设计如下三个层次的练习：

套餐A：求下列圆柱的体积

①圆柱的底面积为5平方分米，高2分米；

②圆柱的底面半径2厘米，高3厘米；

③圆柱的底面直径6厘米，高3厘米；

④圆柱的底面周长12XC56分米，高2分米。

套餐B：右图的圆柱形钢管长4米。如果每立方厘米钢重7.8克，这根钢管重多少千克?

套餐C：在一个圆柱形储水桶里，把一段半径是5厘米的圆钢全部放入水中，水面就上升9厘米；把圆钢竖着拉出水面8厘米长后，水面就下降4厘米。求圆钢的体积。

这样从教材和学生的实际出发，充分考虑到学生的差异，在练习数量和质量的要求上做一些机动、有针对性的设计，从而使练习有坡度，由易到难、从简单到复杂，从基本练习到综合练习，再到实践练习、开放练习，使每个层次的学生都有事可做。

二、“深挖型”练习

课本中提供的习题，一般都是基本练习，如果我们仅限于就题论题，学生在练习中获得的体会必是肤浅的，如果我们能把握习题的特点，挖掘出习题的内在潜力，适时适度地进行发散性、提高性的讲解与分析，必将会大大提高课堂教学质量，提高学生对知识的深度把握。

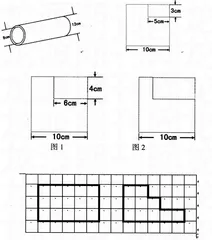
如三年级下册《补充习题》中有这样一道题：从边长10厘米的正方形中去掉一个长5厘米、宽3厘米的长方形后，得到如下图形。它的周长是多少厘米?与原来正方形的周长相等吗?

题目出示后，学生一般都会将围成这一图形的6条线段长度相加：10+10+-(10-3)+5+3+(10-5)=40(厘米)，讲到这儿，一般就会就此打住，似乎完成了教学任务。但为了培养学生运用知识解决问题的能力，进一步提高他们的思维能力，我又作了如下系列的深挖练习：

1　如果剪去长6厘米、宽4厘米的长方形(如图1)，周长与原来正方形的周长相等吗?如果剪去一个长宽都不知道的长方形呢?(如图2)

2　观察下面的两个图形，想一想，要求右边图形的周长，怎样计算比较简便?

如果每个小方格的边长是l厘米，右边图形的周长是多少厘米?先解答，再在小组里说说你的解题方法。

通过这样的深挖练习，让学生初步学习通过平移将它转化为正方形来解决，渗透“转化”的思想，从而初步学会用“转化”的策略解决简单的问题，提高分析问题和解决问题的能力。

三、“开放型”练习

为适应学生个性，满足不同学生的需求，数学练习设计要有开放性和探索性，让数学活动成为—个生动活泼、富有个性的过程，让学生在解决问题的过程中养成积极探索和力求创新的态度。

如我们学习了比例后，设计了这样一道题：下面的四个数能否组成比例?把组成的比例写出来?

6、4、18和12

学生写出的答案可能是不一样的：6：4=18：12.4：12=6：18……教师进一步启发学生：这些答案都对吗?你最多能写出几个?你有什么发现?

这样的练习设计，不但巩固了所学的内容，而且学生的学习情绪高涨，使学生乐于交流，乐于表现自己，同时创新思维得到了更好的发挥。

练习设计是—个永恒的话题，在练习的设计中，我们要关注学生个性，正视学生差异，巧妙设计练习，促进学生更好更快地发展。