追寻数学本质 实施单元整体教学

单元整体教学是近年来基础教育课程改革的重点之一，也是一线教师关注的话题。如何进行有效的单元整体教学？如何在教知识的同时，触及数学的本质，构建知识体系，进而提升学生的数学思维能力，培养学生的核心素养呢？笔者从特级教师夏永立的“加减乘除是一家”一课中撷珠拾贝，从他课堂教学的“简”，领略单元整体教学的“真”，体会如何在返璞归真、大道至简中追寻数学本质。

一、一条数线寻本质

（教师出示0）

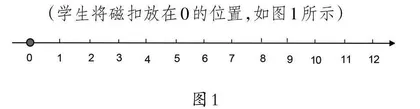
师（出示一条数线）：你能在这条数线上找到0的家吗？

生：在这里。

（学生将磁扣放在0的位置，如图1所示）

（教师出示0+1）

师：它原来的家在哪里？你能找到它的新家吗？

生：我只要把磁扣从0向右跳1格，也就是0+1=1，新家就是1了（如图2所示）。

师：如果它想回到原来的家，又该怎么跳？

生：向左跳1格（如图3所示）。

师：看着刚才跳动的过程，你能写一道什么算式？

生：1-1=0。

师：刚才是一格一格地跳，还可以怎么跳呢？

生：还可以两格两格地跳，或者三格三格地跳……

（师板书：2+2+2+2）

师：它是谁？它原来的家在哪里？怎么跳可以找到新的家？拿出作业单，试着画一画你不同的想法。

（学生画图，如图4所示）

【赏析】《义务教育数学课程标准（2022年版）》指出，几何直观有助于把握问题的本质，明晰思维的路径。它可以把复杂的数学问题变得简明、形象，可以帮助学生直观地理解数学，也可以让直观操作和理性认识建立联系。因此，几何直观在整个数学学习过程中发挥着重要的作用。在教学中，夏永立老师借助一条数线，将数与形结合起来，将算式与图形结合起来，将加减法联系在一起，让学生在一条数线上看到整个小学阶段所要学习的运算的本质。学生不仅知道加法和减法的本质：加法的本质就是计数单位的累加，减法的本质就是计数单位的递减，还能看到加法与减法之间有着互逆的关系。整节课，夏老师用一条数线，发展了学生的几何直观能力，帮助学生追寻数学本质，构建知识体系，在潜移默化中培养学生的核心素养。

二、两种跳动建联系

（教师出示：0+1=1和1-1=0）

师：比较这两道算式，你觉得刚才的跳动有什么不一样？

生：方向不一样。

生：加法是往右跳，减法是往左跳，方向刚好是相反的。

师：它们有没有相同的地方？

生：都跳了1格。

生：其实就是跳动的格子数是一样的。

师：你真善于总结，由加法算式可以想到减法算式，那你认为加法和减法之间有没有关系呢？

生：我认为加法和减法有关系，减法是加法的逆运算。

师：对，加法和减法是互逆关系。

……

（教师出示：2×4=8和8÷2=4）

师：依据刚才的经验，比较这两道算式，你觉得乘法和除法又有什么关系？

生：它们跳动的格子数也是一样的，但是跳动的方向不一样。

生：具体地说，乘法是往右跳，除法是往左跳，跳动的方向是相反的。

生：乘法和除法也是互逆关系。

【赏析】两道算式、两种跳动，将加法与减法、乘法与除法紧密地联系起来。对于低年级学生来说，想说清楚什么时候用加法、什么时候用减法比较容易，可是要说清楚二者之间的联系却不是一件容易的事。但是夏永立老师用两种不同方向的跳动，不仅让学生建立加法与减法之间的联系、乘法与除法之间的联系，而且体会到加法与减法是互逆关系，乘法与除法也是互逆关系。在教学中，教师要教给学生最核心的知识和概念，要让学生抓住知识之间的联系，帮助学生构建知识体系，实现知识的迁移，使教学更有价值。夏老师用左右两种跳动，抓住运算的本质进行教学，形象直观地让学生的数学思维可视化，让单元整体教学更高效。

三、三个问题见整体

师：请你思考一下哲学家们提出的三个问题：我是谁？我从哪里来？将来我要到哪里去？

生：我叫某某，来自某地，我的理想是当一名医生。

……

师（出示0）：我是谁？

生：我是0。

师（出示0+1）：我是谁？原来的家在哪里？怎样跳动就可以找到新家？

生：我是0+1，原来的家在0，向右跳动1格后就变成了0+1，新家是1。

师（出示0+3）：我是谁？原来的家在哪里？怎样跳动就可以找到新家？

生：我是0+3，原来的家在0，向右跳动3格后就变成了0+3，新家是3。

师（出示2+4）：我是谁？原来的家在哪里？怎样跳动就可以找到新家？

生：我是2+4，原来的家在2，向右跳动4格就变成了2+4，新家是6。

师（出示2+2+2+2）：我是谁？原来的家在哪里？怎样跳动就可以找到新家？

生：我是2+2+2+2，原来的家在2。

生：我有不同的想法，我认为原来的家在0，只要向右两格两格地跳，跳4次就可以找到新家8了。

师：我们要给说错的同学掌声，因为他的错误让我们对知识有了更深入的理解，因为说着说着就会了，错着错着就对了。

……

【赏析】老子在《道德经》中说过：“万物之始，大道至简，衍化至繁。”所有问题的出现都有它的原点。夏永立老师将三个问题贯穿于整节课中，学生一开始只是从字面意思上理解，一一说出了姓名、地址和理想。但是，随着课堂的推进、学习的深入，夏老师对每一个关键知识都提出这样的三个问题，让学生体会：不仅生活中我们要思考这三个问题，学习知识亦是如此。如果我们的眼睛仅仅盯着知识的本身，最终只会“只见树木，不见森林”。这三个问题的引领，学生不仅知道了知识的本源，而且经历了知识的产生、形成和发展的过程。因此，单元整体教学的设计，对于每一个知识，我们要知道它是什么？它从哪里来？将来要到哪里去？需要把知识置于整个知识体系中加以思考，追本溯源，不仅注重知识的“生长点”，还要注重知识的“延伸点”，引导学生感受数学的整体性。这其实就是夏老师所强调的单元整体教学要有“大视野”“大格局”。

四、四个箭头围一家

师：刚才，我们是一格一格地跳，还可以怎么跳？

师（出示2+2+2+2）：我是谁？原来的家在哪里？怎么跳就可以找到新家？拿出作业单，画一画吧！

师：由这道连加算式，你能想到哪一道乘法算式？

生：2×4=8。

师：你是喜欢写加法算式还是乘法算式呢？为什么？

生：我会选择乘法算式，因为乘法算式比较简洁，加法算式比较复杂。

师：你认为乘法是怎么“长”出来的？

生：乘法是由连加的算式“长”出来的。

师：现在的家在8，原来的家在0，它想回到原来的家，你能记录下它跳动的轨迹吗？

（学生演示）

师：根据刚才跳格子的过程，你能写出哪道算式？

生：8-2-2-2-2=0。

师：除了可以写减法算式，还可以写什么算式？

生：还可以写除法算式，8÷2=4。

师：你认为除法算式又是由哪道算式“长”出来的？

生：除法是由减法“长”出来的。

师：除了刚才的跳动，你还能想到哪些跳动的方式，先写出加法算式，再写出由这道加法算式能想到的其他算式。

（学生汇报并板书）

师：通过今天的学习，你认为加法、减法、乘法、除法之间有联系吗？能将它们的关系表示出来吗？

生：由加法可以“长”出乘法，减法可以“长”出除法。加法和减法是可以相互转化的，乘法和除法也是可以相互转化的。

师：加减乘除亲如“一家人”。加减法是低一级的运算，乘除法是高一级的运算（板书如图5所示）。

【赏析】一节课结束后，教师常常会思考：这节课到底给学生留下了什么？教师给学生留下什么东西，板书是最直观的，它就是一个微型的教学设计。在本节课的教学中，师生合作完成板书，特别是结尾处夏老师放手让学生用箭头表示出加法、减法、乘法、除法之间的关系，形成了简单的思维导图。不难看出，学生已经真正清楚了四则运算之间不可分割的关系，正如夏老师用形象的比喻形容的那样，加法和减法是一切运算的源头，是原点，乘法和除法就如同它们的孩子一般，是由加减法生长出来的。由此，亲密和谐的大家庭组成了，学生也逐渐明白，原来之前学过的知识并不是孤立存在的，四个箭头将它们围成了亲密无间的“一家人”。

在教学中，夏永立老师用一条数线、两种跳动、三个问题、四个箭头将看似独立的知识紧紧地联系在一起，整节课“起点低”“素材少”“节奏慢”，却让我们清晰地看到了一张知识网络图，这张知识网络图也一定会深深地印在了学生的脑海中，也让我们对单元整体教学有了新的认识和思考。因此，高效的课堂不需要华丽的课件和辅助工具，就这样以最朴实的师生对话、真切的问题交流，让学生慢慢体会数学的本质，找寻数学的原点，感受数学的魅力。

（作者单位：安徽省肥东县实验小学）