以学定教突破搭配问题难点

排列问题与组合问题同属于“搭配问题”，是小学数学综合与实践学习领域的重要内容。在人教版小学数学教材中，这个内容编排在二年级上册和三年级下册的“数学广角”板块。理解排列问题的“有顺序”和组合问题的“无顺序”，正确辨识并解决这两类问题是学习难点。本文基于以学定教理念，以二年级上册《搭配（一）》例2（组合问题）的教学为例，探析突破难点的教学策略。

一、分析学情，确立辨识排列问题与组合问题的学习路径

明确学生的学习难点是设计、实施有效教学的前提。教师要结合实际学情制定具有针对性和可行性的教学方案，确立有助于学生辨识排列问题与组合问题的学习路径。

常规教学中，教师往往会发现这样的现象：有的学生由于先学习的是排列问题，便将所有“搭配问题”归类为排列问题，用“交换位置法”“固定十位法”“固定个位法”等方法解决；有的学生认为解答组合问题的“连线法”更加简便、直观，产生只用这种方法解题的倾向。究其原因，是学生不能清楚地辨识排列问题和组合问题，没有真正理解排列问题的“有顺序”和组合问题的“无顺序”。如果教师不注重引导学生辨识这两个概念，整个主题单元的教学就可能功败垂成。

二年级上册教材首先编排的是排列问题（例1）及其解决方法，学生学习后能够初步形成有序、全面思考问题的意识，在此基础上学习组合问题（例2）更有利于学生辨识两者的区别。基于这样的考量，笔者确认例2的教学重点应该包括理解排列问题与组合问题的差别。由此，笔者设计了如下学习路径。首先，整合教材中的两道例题，创设情境，组织小组学习活动，让学生在同一个时间段先后经历一次解决排列问题的过程和一次解决组合问题的过程，在对比中体会两类问题的差别。接着，从字面意义上向学生说明“有顺序”指结果会受到顺序的影响，“无顺序”指即使改变顺序，结果也不受影响。然后，改编教材中的练习题，组织学生先判断改编后的练习题是排列问题还是组合问题，再集体作答并验证，让学生深入交流、体会两类问题的差别。最后，布置“握手问题”的实践性作业，让学生在活动中理解“握手问题”属于组合问题，提高利用所学知识解决实际问题的能力。

二、小组共学，自主探析排列问题与组合问题的差别

教学例2前，为了引导学生明确排列问题与组合问题的差别，笔者将二年级上册教材第97页的例1与第98页的例2整合，形成包括以下两个问题的例题：从1，2，3中任意选取两个数字组成两位数，能组成几个两位数？从1，2，3中任意选取两个数字求和，得数有几种可能？

教学例2时，笔者设计复习引入环节，先出示第一个问题：“从1，2，3中任意选取两个数字组成两位数，能组成几个两位数？”由于有了学习排列问题（例1）的基础，学生能比较容易地得出“能组成6个两位数”的正确答案。接着，笔者出示第二个问题：“从1，2，3中任意选取两个数字求和，得数有几种可能？”一部分学生不假思索地回答“6种”。另一部分学生提出质疑：“我觉得不是6种，因为‘1+2’和‘2+1’的得数都是3，只能算一种。”笔者顺势引导：“两位数的大小与其个位、十位上数字的位置紧密相关，求和的问题与此情况相同吗，让我们通过动手操作对比分析。”然后，笔者要求各小组拿出1，2，3三张数字卡片，组员一和组员二共同负责摆卡片，组员三记录摆出的两位数，组员四计算并记录摆出的两张卡片上的数字之和，最后四名组员共同对比观察记录的内容，看看有什么发现。小组共学后，学生发现组成的两位数有6个，而求和的计算结果只有3种。笔者肯定了小组学习的成果，并提问：“同样是从3个数字中选择2个，为什么两个问题的作答结果不同呢？”一个小组举例说明：“1+2和2+1的得数都是3，1+3和3+1的得数都是4，2+3和3+2的得数都是5，去掉一样的结果，只剩下3种结果。”另一个小组补充：“数字1和2组成的两位数是12，数字2和1组成的两位数是21，相似的情况还有13和31，以及23和32。也就是说，组成的所有两位数都不相同，没有‘去掉’的情况，所以结果有6个。”笔者追问：“同学们仔细观察，我们改变两张数字卡片的摆放顺序后，组成的两位数和求和的结果有没有发生相应的变化呢？”学生交流后得到一致的结论：当数字卡片的摆放顺序发生变化，组成的两位数变了，而求和的结果不变。最后，笔者引导学生总结：像组两位数这样，结果会受到顺序影响的问题属于排列问题，它的特征是“有顺序”；像求和这样，结果与顺序无关的问题属于组合问题，它的特征是“无顺序”。学生领悟之后，笔者补充说明：“我们遇到‘搭配问题’时要先结合已有的数学信息举例分析顺序是否对结果产生影响，进而由部分知整体，判断问题是‘有顺序’的还是‘无顺序’的。‘有顺序’的问题通常用‘固定十位法’‘固定个位法’‘交换位置法’解决，而‘无顺序’的问题通常用‘连线法’解决。”由此，笔者引入组合问题常用解法“连线法”的教学。

这样教学，学生明确了区分排列问题与组合问题的关键，知道要从结果出发，思考顺序对结果是否有影响，从而对所学知识形成了更深入的理解。

三、技术赋能，强化对排列问题与组合问题差别的认识

教师可以通过多媒体技术整合教学内容、丰富学习资源，给予学生视觉上的刺激，强化他们对排列问题与组合问题差别的认识，使其能够融会贯通地解决“搭配问题”。

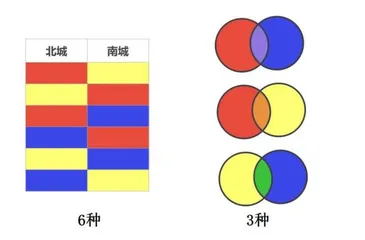
学生初步把握了区分排列问题与组合问题的关键点以及解决问题的步骤后，笔者引导学生巩固运用。二年级上册教材第97页“做一做”的题目是：从红、黄、蓝3种颜色中选出2种颜色，给地图上的2个城区（北城和南城）涂上不同的颜色，一共有多少种涂色方法？笔者以这道题为基础设计针对本节课内容的拓展练习题，并在设计中巧妙融入信息技术。改编后的练习题如下：从红、黄、蓝3种颜料中选出2种颜料混合调色，可以调出多少种不同的颜色？课堂上，笔者先引导学生作答原题并展示学生的作答结果，帮助学生回顾旧知，再呈现改编后的练习题，组织学生小组讨论，判断混色问题是否与顺序有关。一个小组判断：“这个问题是‘无顺序’的，因为不论是在红色颜料中加入黄色颜料，还是在黄色颜料中加入红色颜料，最后调出的都是红色颜料和黄色颜料的混合液。”另一个小组补充：“也就是说，加入不同颜色颜料的顺序不会影响最后的调色结果，所以这个问题与顺序无关，是组合问题。”随后，学生用“连线法”解决了问题。笔者适时用动画演示三种颜色两两混合的结果，验证学生的作答。最后，笔者并列展示原题和改编题的结果（如下图），让学生通过对比深入体会两类问题的差别。

以上教学，笔者把直观的色彩作为素材设计相关的练习题，激发了学生的探究兴趣，使学生加深了印象、深化了理解。

（作者单位：荆州市公安县竹溪小学）