积累活动经验 助力模型生长

小学数学“搭配问题”包括简单的排列问题与组合问题。排列与组合在现实生活中应用广泛，是学生后续学习统计与概率知识的基础，也是发展学生抽象能力和逻辑思维能力的优质素材。本期，我们从模型建构、问题类型识别、单元整体设计等角度，依托不同课时内容谈“搭配问题”教学策略。

《搭配（一）》是人教版数学二年级上册的内容。例1是简单的排列问题，其教学旨在通过操作、观察、猜测等活动，引导学生探究简单事物排列数的基本思路与方法，体会搭配时有序思考、全面思考才能不重不漏。

一、关注操作细节，积累活动经验

“搭配问题”比较抽象，教师引导学生运用学具有序操作既能促进其有序思考，又能使搭配的结果有序呈现。教学中，笔者对比呈现学生无序操作与有序操作的过程，引导他们细致观察与思考操作过程，积累“搭配”的活动经验。

教学伊始，笔者出示问题情境：从1，2，3中任意选取两个数字组成两位数，可以组成哪些数？学生用数字卡片摆数并记录结果。然后，笔者呈现“①12，32，13，12，21，31；②12，13，21，23，31，32；③12，21，13，31，23，32”三种结果，并分别播放三名学生第一次和第二次摆卡片的视频，引导学生观察他们的操作步骤有什么相同点和不同点。学生发现：相同点是3名同学第一次操作都选择卡片1和卡片2摆数，不同点是第二次操作时A同学摆出12后，先将这两张卡片放回原位，再重新拿出卡片2和卡片3，摆出32；B同学摆出12后，没有挪动卡片1，只将卡片2放回去，又拿出卡片3，摆出13；C同学摆出12后，直接调换这两张卡片的位置，摆出21。笔者继续展示三名学生第三次和第四次操作的视频，让学生说一说有什么发现。一名学生回答：“A同学第三次拿出卡片1和卡片3，摆出13，第四次拿出卡片2和卡片1，摆出12，记录后发现重复了，又摆成21。B同学将卡片2定在十位，摆出21和23。C同学用卡片1和卡片3摆出13和31。”另一名学生补充：“A同学第四次摆的时候犹豫了一下，他可能记不清哪些数字已经摆过了，这样摆很容易出错。B同学和C同学的摆法是有顺序的。”笔者追问：他们的摆法有怎样的顺序？你能给他们的摆法取个名字吗？学生为B同学的摆法取名“固定十位法”，为C同学的摆法取名“交换位置法”。最后，笔者让学生猜测B同学和C同学接下来如何操作，并继续播放视频验证学生的猜测。

笔者通过“慢放”学生的操作过程并在细节处追问，为学生搭建了可视化思维框架，让他们清楚地看到无序操作的“繁”与“乱”，体会到有序操作的“简”与“全”。

二、借助多元表征，学会有序思考

学生的思维水平、知识基础有差别，经过前面的操作环节，有的学生仍然需要借助具体的操作活动，才能不重不漏地找出搭配结果；有的学生则能顺利将操作经验提升为抽象思考，即使不操作，也能借助其他方式找到答案。基于实际学情，笔者先创设相似的问题情境“从7，5，9中任意选取两个数字组成两位数，能组成几个数？”，允许学生以不同的方式表征搭配过程，再通过不同方法的对比促进学生将活动经验数学化，掌握有序思考的方法。

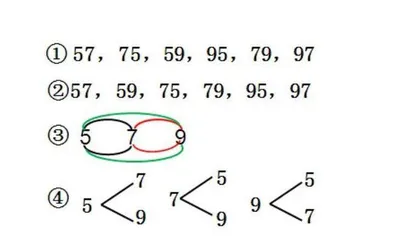
有的学生借助卡片摆一摆，有的学生在纸上画一画、写一写、连一连。随后，笔者呈现如下四种作答结果，并提问：哪些方法看起来不一样，其实是一样的？

通过交流，学生达成共识：方法①和方法③是交换位置法，方法②和方法④是固定十位法。笔者追问：为什么方法③中5和7之间要连两条线？为什么用三种颜色做标记？方法④中第一个5为什么只写一次？从5分出两条线是什么意思？学生讨论后汇报：方法③中5和7之间连两条线是因为两个数字交换位置后可以组成两个两位数，用不同的颜色做标记是为了让人一眼就看出搭配顺序；方法④中第一个5只写一次表示固定十位上的数，这样可以为个位分别搭配两个数字，所以分出两条线。笔者引导：你能看出这两种方法一共组成了几个两位数吗？学生回答：方法③连一条线能组成一个两位数，同一种颜色的线表示正、反各连一次后组成两个两位数，有三种颜色的线，说明组成了6个两位数，这个过程可以用“2+2+2=6”表示；方法④十位上的数字可以分别固定为5，7，9三个数字，每个数字固定在十位时都能搭配另外两个数字，所以一共可以形成6个两位数，这个过程可以用“3×2=6”表示。笔者追问：加法算式中的2分别表示什么意思？乘法算式中的3和2各表示什么？你能在图中指一指吗？

以上教学，学生通过对比不同的解决问题方法，寻找不同方法之间的区别和联系，进一步理解了“有序”。

三、设置梯度任务，促进模型建构

排列问题和组合问题结构相似，“是否与顺序有关”是识别两类问题的关键。情境是否熟悉、问题是否具备典型特征都会影响学生对问题类型的识别。基于此，笔者设置如下梯度任务让学生类比学习，从不同背景的现实问题中抽象出排列问题数学模型。

下面哪些问题能用本节课学习的搭配方法解决？先判断，再作答。

①啤酒鸭、炸子鸡、盘鳝是宜城的特色菜。如果将这三盘菜摆成一排向游客展示，有多少种摆法？

②小明、小红、小刚比赛拍球，每两人比一场，一共要比几场？

③王老师要将《自然奥秘》《数学迷题》《儿童文学》三本书送给小丽、小清和小红，每人1本，一共有多少种不同的送法？

④从7，5，6，9中任意选取两个数字组成两位数，能组成几个数？

学生发现：问题①③④都能用搭配数字的方法解决，而问题②不能用搭配数字的方法解决，因为“交换位置”后还是这两个人比赛，位置的交换不能产生新的比赛。问题②为后续组合问题模型的学习埋下了伏笔 。

解决问题①时，很多学生将三种菜简化为三个不同的字母或图形，并说明这样表示更简洁明了。解决问题③时，学生都是先将三本书的题目或三名学生的名字写在一行（列），再进行搭配。笔者追问学生为什么这样写，学生回答：送书时，可以“人取书”，也可以“书送人”，写成一行（列）相当于固定十位或个位上的数字，这样表示很有序，有助于做到不重不漏。对于问题④，有的学生汇报用连线法需要用到6种不同颜色的线，每种颜色的线连出2个两位数，可以用“6×2=12”计算搭配结果；有的学生认为4个数字都可以固定在十位，每个十位上的数字可以分出3条线，所以用“4×3=12”计算搭配结果。笔者引导：与前面用7，5，9组数相比，这道题多组成了几个两位数？多的是哪几个数？学生发现：连线时6要分别与5，7，9连两次，组出来的两位数有65，56，67，76，69，96（与之前相比多组出来的数）；用固定十位法解题时，分别把5，7，9固定在十位，个位上会各多出现一种搭配，所以多组出56，76，96三个数，而6也可以固定在十位，这时个位可以搭配5，7，9三个数，又多组出65，67，69三个数；还有的学生指着“分叉图”说：“好奇妙！只增加6这一个数字，5，7，9上都会再长出1个枝丫，6自己还可以长出3个枝丫。”在判断问题能否用搭配数字的相关方法解决的过程中，学生强化了对排列问题模型的识别。

（作者单位：宜城市窑湾小学）