问题导学构建小学数学探究式课堂探索

摘  要：“双减”背景下如何实现课堂的减负增质，教师利用问题导学，激发学生的学习兴趣，构建小学数学探究式课堂，就是一条有效途径。文章以数学特级教师吴正宪老师和教学实践为例，从四个方面去论述，即激趣引入，巧妙设问；初始探究，适时提问；深入探究，不断追问；拓展探究，反复叩问。它致力于以问题引领自学，以问题引领合作，以问题引领生成，实现高效课堂。

关键词：关键问题；导学；探究式课堂；小学数学

美国著名科学家加波普尔说：“科学与知识的增长，永远始于问题。”问题是教学的载体，它推动着课堂教学的进程。不是知识或结果促进学生的认知发展和思维发展，是“问题”促进学生思维的启动与深入。因此，教师要认真分析教学内容，深度整合教材，以关键问题为主线，直击核心素养，质疑问难，设计教学环节，画龙点睛般不断追问，直击算理算法，直击数学本质，引领学生主动参与学习，通过学生一系列的思维活动、操作活动，实现生生交流、师生交流，质疑，推理，归纳总结，达到思维的升华。

一、激趣引入，巧妙设问

（一）创设情境，发现问题

良好的开始是成功的一半。在一堂课的引入阶段，如何创设情境引导学生发现问题是课堂开课的一个关键。利用情境呈现给学生生动有趣且有挑战性的数学信息，能有效地激发学生学习数学的兴趣，启迪学生的思维。对同一教学内容的情境教学有很多种，教者要有取舍，选择最有价值的情境，唤起学生强烈的问题意识，去分析和探究数学问题。数学特级教师吴正宪老师的《小数除法》，创设的情境不用情景图，而是讲故事，让每个孩子记下来，教师并没有告诉学生怎么记录。“甲乙丙丁４人聚餐付出１００元，找回３元，ＡＡ制买单，每人应该平摊多少元？”有的孩子把教师讲的故事全部记录下来，有的孩子只记了几个关键信息，有的孩子直接列式。她是让学生记录故事中的数学问题，是把现实情境数学化，除去原始情景保留数学问题，让来自生活的数学情景唤起孩子学习的兴趣，让学生经历一个生活数学化的过程。这样的开课引入，让人们耳目一新。接着吴老师又问：“如果你是甲乙丙丁中的一人，你最关心什么？”学生说：“我应付多少钱？”这样引趣启思的情境导入形式，是教者在教学生学会用数学的思维思考现实世界，直指要解决的本质问题，这就是最好的情景引入式教学。

（二）问题聚焦，导入学习

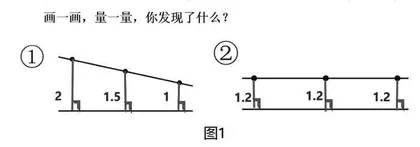
核心素养是教师上好每一堂课的目的、方向和标准。有了明确的目标，教学活动的设计才不会走偏，课堂教学活动才会扎实有效。精准巧妙地设计导学问题应该从学生学什么，怎样学，学到什么水平等高度来思考。例如在教学《认识平行》时，笔者首先思考这个内容的素养点是培养学生的空间思维能力，学会判断两条直线是否“互相平行”，并能借助直尺等工具画出“互相平行的直线”，使学生感受生活中的“平行之美”，体验“空间与图形”学习的乐趣。为此，笔者设计并瞄准认识“什么是平行”这个关键问题展开教学。从“垂直”的教学开始让学生用两根小棒摆不同的情形，到这节课让学生用手势表示两条直线的位置关系，再给这些情形分分类，按是否相交来分，分出了不相交的两条直线互相平行。我觉得还不够，又设计了一组对比题（如图1）。

让学生画一画，量一量，比一比，发现了“相交的两条直线之间的距离不相等，而不相交的两条直线之间的距离处处相等”，让学生充分理解什么情况下两条直线互相平行。这样在学生的大脑中，就定格了平行线图像。有了这样的关键问题导学，直击了这节课的核心素养点，培养了学生的空间观念。

二、初始探究，适时提问

（一）适时提问，引领探究

开课以后，如何把问题探究引向深入？适时提问就是一种有效的策略，通过适时提问，不断激励学生进行积极思考。如何以问题为载体，启迪学生思维呢？吴老师的做法是让问题牵引课堂探究。①４人，花９７元，平均每人多少钱？②当用竖式计算出现２４元余１元，“１元”怎么分？③将余下的２角怎么分？④小数点怎么站？竖式怎么写？这些问题让孩子自己提出来，学生的学习才能真正开始。在老师的引导下放手让学生去发现问题，不断提出问题、分析问题，最后解决问题。让学生从“分钱”到“分数”的学习，实现从生活经验到数学本质。通过孩子的交流、讨论、质疑等一系列活动，使孩子明确小数除法的本质其实就是分计数单位。大的计数单位不够，就化成小的计数单位继续分，强调没分完就继续分，成功地将一节枯燥的计算课变成了一堂生动有趣的“分分分”的课堂。这样的课堂，引导学生多提问、敢质疑，注重培养和发展学生的核心素养，追寻了本真。

（二）适时提问，引领合作

问题是激发学生思考的原动力，有了小疑惑就有了小的进步，有了大疑惑就有了大的进步。正是因为通过对所产生的疑问进行不断地思考和探究，才会逐渐透过数学知识的表层深入内里，自觉自发地去了解数学问题的本质并找到解答的正确途径。例如教学循环小数时，为激发学生学习兴趣，教者在抛出问题“关于循环小数，你们想知道什么”，引导学生讨论。学生提出“什么是循环小数？循环小数是怎样产生的……”教者设计了三个活动解决这些问题。活动一：看书思考这些小数都是循环小数吗？２．０８０８……０．３３３ ０．４３６６……１２．０５３０５３…… 活动二：这些循环小数的书写是否规范？有没有简便写法？活动三：你还知道什么？学生看完书后，４人小组分工合作，共同研讨。请学生上台分享，让小组合作不流于形式，不是作秀。问题从学生中来，再由学生去解决，生生交流，教师适时点拨。教者充分信任学生，遵从他们的认知规律，尊重他们的想法，分享他们的喜悦，努力使课堂成为学生“主动学习、主动探究”的乐园。例如笔者在教学画平行线时，当已经教给学生画平行线的步骤时，请每桌的１号学生发号施令，观察２号同学画平行线，并发口令“一挨、二靠、三移、四画”。再同桌互换，让每个学生都体会一下当指挥者的乐趣和自信。教师要对每个合作小组进行走访，了解各组的学习情况，并适时指导；一同参与小组的讨论交流，与学生进行平等的对话，做学生的合作伙伴。

三、深入探究，不断追问

课堂追问是一门教学艺术，是在教学中常被教师采用的一种有效教学手段，适时不断地进行课堂追问，是教师驾驭课堂的重要体现。教师善于运用追问技巧，可以在潜移默化中突出教学重点，破解教学难点，导向数学本真。

（一）在关键范例处追问

如在教学三位数除以两位数的笔算除法时，学生先试算８４０÷２１，再由学生试讲他是怎样算８４０÷２１。在这里，我追问了４个问题：（１）为什么商的最高位会在十位上？（２）你怎么想到商４？（３）你是怎样确定刚好商４？（４）而在８４０÷２４时，又一个追问：为什么不商４，改商３呢？通过这样的追问导学，总结出笔算除法的步骤：“定→估→试→调”，让学生很快明白算理算法。试商４，用４去乘原除数是９６，８４减９６不够减，说明商４大了，改商３；用３去乘原除数是７２，８４减７２够减，余数是１２，余数比除数小，说明商３对了。这样对标导向算理算法，让学生知其然还要知其所以然，让学生的思考更加准确有效。

（二）在画图操作处追问

如在教学画平行线时，笔者设计了４个追问：（１）用现成的工具能描平行线吗？（直尺、数学书、文具盒等）（２）如果我给直线外点一点，给已知直线画平行线，还能用现成的工具吗？（３）用一种工具能画平行线吗？（４）为什么要给它找一个依靠？通过动手操作中的追问，以启发学生深入思考知识的本质，让数学教学更加精彩。

（三）在想象建模处追问

如笔者在教学１公顷有多大时，为了在学生头脑中建立１公顷的表象，笔者不断追问：“一间教室大约５０平方米，１公顷里包含了多少间教室？想象２００间教室那是多大呀。如果拿着１平方米的正方形去铺１公顷，每排铺１００个，想象会铺到哪里去？要铺１００排，又铺到哪里去？要铺满１公顷的大正方形，要铺多少个？１００００个那是多大呀！”学到这里学生对１公顷应该有点感觉了，再看学生很熟悉的中岩广场，它的面积大约就是１公顷。教师带着学生想象着围绕１公顷的四周走一走，走完后教师追问：“你走后有什么感觉？”学生纷纷发言，“走了有点累，１公顷很大”。学生找到了１公顷的生活原型做依托，再去估测发展中的学道街小学和周边的几公顷，这样的追问想象使学生的感性认识非常深刻。问题引导，拓展想象，充分挖掘一切可以调动学生思维活跃的因素，发展学生的空间观念，追寻本真。

四、拓展探究，反复叩问

（一）反复叩问，归纳算理

东北师范大学教务处副校长郑燕林教授曾说：“如果一个孩子习得知识，掉进一个坑里，他会想办法出来；如果一个孩子习得智慧，他根本不会掉进去。”例如吴老师《小数除法》的这节课，在探究小数除法的算理时，学生很容易就算出：９６÷４＝２４余１，每人是２４元吗？显然不是，剩下的１元怎么办？谁出都不公平，怎么做才公平呢？只有把１元破坏掉，变成１０角，就活了，又可以分了，将余下的２角换成２０分，又可以分了，就这样在学生已有的经验上找准知识连接点，将复杂的算理变成简单的“分分分”，从而体会小数点在小数除法中的重要作用，它就像孙悟空的定海神针，教师要由衷感谢小数点，自主将分的过程用竖式表达出来，再用反复叩问的形式将分“钱”迁移到分“个”、分“米”、分“数”，小数除法的意义由具体到抽象，使学生最终理解了小数除法的本质。在这堂生动有趣的“分物操作”过程中，孩子们的数学运算和直观想象得到了充分的培养，推理思想、模型思想、转化思想、极限思想也渗透其中，知识技能水乳交融，彰显了老师的教学智慧，学生的学习智慧，真正地培养了学生的数学核心素养。

（二）反复叩问，梳理脉络

学习数学不仅要深入理解每一个知识，掌握每一种技能，还需要理解所学内容的结构体系和基本脉络。这就要求教师从宏观角度看清楚整个教材的重点、难点以及各部分之间的联系，明确知识的来龙去脉，抓住本质的东西来组织教学。如在教学“平行”知识时，先要从直线的特点出发，直线具有无始无终的特点，线段是直线的一部分，两条直线的位置关系在同一平面内相交和不相交，不相交就平行。除了用视觉去感知把两条直线无论怎么延长都不相交，还要实际去操作，比一比，画一画平行线之间的距离处处相等。从结构上看，学习直线、线段、射线是为学习垂直、平行做准备；而学习平行的目的是为后面学习平行四边形、梯形、长方体、正方体做准备的。正如法国数学家布尔巴基指出：“数学不是研究数量的，而是研究结构的”，所以我们在教学中如果能够站在一个整体认知高度来教学，对提升学生的思维品质必然会起到事半功倍的效果。

（三）反复叩问，彰显大爱

一节成功的数学课，要把时空有限的课堂变为人人参与、个个思考的课堂，要让每个学生都有所发展，有所收获，真正体现“学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者”的理念。吴老师的课堂以情激情，她能够真正做到从心底关心、欣赏学生，使每一个学生获得成功的体验。如吴老师说：“还有事吗？”“你不理解他的意识吗？”“你来说说你的想法？”“不怕，来呀，不急！”“你们不需要齐刷刷地回答我，可以点点头，皱皱眉，找个合适的姿势坐好。”这些话语不仅体现了教师是真正地尊重学生、爱学生，而且培养了学生的自信心，健全学生的人格。吴老师还非常善于用体态语言来表达对学生的喜爱之情，走入学生的心灵。如：用眼神表达，扶扶肩膀、摸摸头，这一系列自然的行为，细腻地向学生传递着老师的信任，同时也体现了教师对学生深深的爱。

以关键问题引领的结构化教学策略，它致力于以问题为载体，引领学生自主学习、合作学习，直击数学核心素养，直击结构化教学，直击数学本质；教师教学时思路清晰，有条不紊，不再信马由缰。关键问题导学模式可以帮助教师在新课改的路上走得更快更远，也一定会帮助教师打造一个高效的课堂。

参考文献：

［１］ 洪艺萍． 基于数学文化培养小学生数学核心素养的教学策略研究［Ｄ］． 重庆：西南大学，２０２０．

［２］ 蔡鑫． 对基于数学核心素养的小学数学教学改革的几点思考［Ｊ］． 数学大世界（下旬），２０２０（０４）：３７

［３］ 孔凡哲，史宁中． 中国学生发展的数学核心素养概念界定及养成途径［Ｊ］． 教育科学研究，２０１７（０６）：５－１１．

（责任编辑：秦  雷）