单位化思想，使除法问题更有条理

［摘  要］ 除法的意义一般有两种模型：包含除和等分除。教师可以通过“确定单位”“操作单位”“包含单位个数”等教学手段，引导学生分析问题，使除法问题的解决变得有条理、有顺序。

［关键词］ 包含除；等分除；单位化；结构化

度量意识是学生在测量中体现的数学素养，在解决除法问题时也有重要作用。为了方便表达与交流，在比较某些事物时人们常常设置一个标准量，用“单位”来量化研究对象，目的在于简化解决问题的思维过程［１］。刘加霞教授称这种解决问题的思维策略叫“单位化思想”。单位化思想有利于学生阐明思维过程，使思维有条理。单位化思想隐藏在“包含除”中，不易被提取出来使之明确化，导致学生在解决复杂的小数、分数问题时容易混淆。

一、除法的两种模型

除法就是不断地减相同的数，把相同数看作一个单位，有几个这样的单位，商就是几。它与单位化思想不谋而合。

除法的基础是平均分，从分的过程来看，有两个不同的模型，被研究者称为“包含除”和“等分除”［２］。平均分的过程体现单位化思想，比如：12个苹果，每3个装一盘，可以装几盘？3个一盘，3就是题目中的单位，用这个单位去度量12，看12里面包含几个3，学生很容易想到除法就是“不停地减去相同的数”。在教学整数除法时，教师要有意识地引导学生经历分的过程，让学生通过操作“每几个1份”，加深对“单位化思想”的理解；在教学小数除法、分数除法的意义时，教师要引导学生迁移知识，用除法的意义来理解新问题，比如2÷1/3，学生不会认为是把2平均分成1/3份，而会思考2里面包含几个1/3。

“等分除”更多体现“平均分”，几个几个地分，实际上是单位化思想［３］。比如“分物游戏”：15根骨头，平均分给3只小狗，有几种不同的分法？由于数字不大，学生说每只小狗分5根，实际上就是5根5根地分，5根是一个单位，这种分法是“包含除”。学生如果1根1根地分，会发现还剩很多，就大胆地调整为3根3根地分；然后对剩下的骨头1根1根地分，可以说每一次“平均分”都有单位化思想。每一次调整的过程，学生都在思考“合适的单位”，经历调整“单位”的过程，加深对除法意义的理解。在教学中，笔者发现学生常常根据乘法口诀或生活经验很快得出1份有几个，不再借助“合适的单位”，说明学生已有的知识对学习活动的设计提出了更高要求。

二、教学中的偏颇

部分学生喜欢用“平均分”来解释除法问题。比如，学生学习除法第一课“分物游戏”，这是学生第一次认识平均分，强调要分得公平，每人一样多，应该“平均分”；学习“分数的初步认识”，再一次强化“平均分”的思想，把一张纸平均分成3份，其中的1份用分数1/3表示，因此学生描述一个分数时使用“平均分”；在学习“平均数的认识”时，除了“移多补少”的方法，学生知道把总数算出来再平均分成几份，得到的数就是平均数；学习“小数除法”时，学生用“平均分”就无法解释遇到的新问题。

比如，“谁打电话时间长”的问题：国内电话费0.3元1分钟，笑笑花了5.1元，笑笑打了几分钟？有的学生将算式5.1÷0.3理解为“把5.1平均分成0.3份，每份是多少”，一些学生认为不正确，因为以前平均分成几份时的“几”是整数，现在却是小数。于是笔者引导学生回到题目情境，把0.3元看作1份，看5.1元里包含几个0.3元，有几个0.3就有几分钟。教师引导学生将0.3看作此题中的“单位”，用它去度量5.1，让学生用度量的思想理解除法的含义。教材多个地方强调“平均分”，造成学生对包含除的理解弱化的现象。

三、教材对两种除法的安排

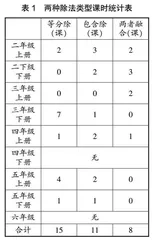
笔者发现教材比较重视“等分除”，对“包含除”较少关注。笔者对北师大版小学数学教材中各年段除法意义相关内容的课时数进行了统计（见表1）。

从总体上看，笔者发现小学阶段关于除法的运算共计34课时，“等分除”有15课时，“包含除”有11课时，两者皆涉及有8课时。而且在整数、小数、分数的除法教学时都是先教学“等分除”，再教学“包含除”，最后进行融合学习。可见，教材力求平衡除法“等分除”与“包含除”两种意义，不断循环，以促进学生对除法意义的认知螺旋上升。

单从某一年级看，又有偏向，特别是三年级下册有8课时关于除法的内容，如表2所示，其中有7课时都是“等分除”［４］。这一单元8课时内容中，有6课时出现“平均分”。四年级只有2课时涉及“包含除”，数量较少，导致“平均分”在学生大脑里占据主导地位。学生对除法的理解习惯性认为是“等分除”，这个单元具有推动作用。但到了五年级，学生学习小数除法时，无法理解复杂算式的意义，无法解决复杂的问题。在实践教学中，学生学习的困难集中出现在“人民币兑换”这一内容。

四、单位化思想的实践

学生在现实生活中较少涉及人民币兑换的知识，与其他小数除法的问题相比，在解决这类题时出错率高。教学后，笔者针对常见的人民币兑换问题对所教学的两个班级进行测试，一班36人，二班47人，正确率统计如表3所示。

从结果看正确率最高的是一步计算，一班正确率达到100%，二班正确率是95%，明显看出用乘法解决人民币兑换问题最好。用除法解决问题时，两个班的正确率分别下降到72.3%和86.1%，情况不是很好。在两步混合计算中，两个班的正确率都在83%左右。74000日元与100日元兑换多少人民币，二者单位一样，大部分学生利用单位化思想解决，只有少数学生不明白。如果汇率呈现100元的币种与较大数额的币种不一样，需要转化。如对于“100泰铢换23.28元人民币，3400元人民币换多少泰铢”，学生正确率约75%。因此，教师要引导学生对两类题进行强化训练，一类是用除法解决的问题，另一类是兑换率以100为单位呈现的题。为了让学生真正理解其中的道理，用单位化思想解决问题时条理更清晰，笔者开展了教学实践。

情境问题：淘气和爸爸去香港迪士尼玩，成人票539港元，儿童票383港元，两人门票共折合人民币多少元？（当时1元人民币兑换1.15港元）

生1：以前我用“单位进率”的思想来做，单位大化小用乘法，小化大用除法。但发现有些题不能用这种方法，比如，1元人民币换多少港元，1港元换多少人民币，搞不明白究竟用乘法还是用除法，要思考好一会儿。

生2：需要明白题目的意思才行，不能套用公式。门票是港元，就把1.15港元作为1份，看总数里有这样的几份，就能换几个1元人民币。

生1：你的意思是把1.15港元作为一个标准，去度量539港元，看539里面包含几个1.15，就知道能换多少人民币。哦，那我知道了，用除法做。

为了强化单位化思想，笔者呈现了一组两步计算的题。

情境问题：“五一”假期明明一家去日本旅游，5天共花了36000日元，折合人民币多少元？（当时100日元兑换人民币6.42元）

生3：我以100日元为1份，36000里有这样的360份；再利用份数×每份数=总数，就能得到结果。

生4：我先算1日元兑换人民币多少元，再算36000日元兑换多少元人民币。

为了让学生更容易理解，笔者对每一种方法都画了线段图进行说明，如图1所示。

师：对比一下两种方法，有什么相同的地方？

生5：我发现两种方法都是以“1份”为单位来思考。第一种方法以100日元为1份，第二种以1日元为1份，先算出份数，再乘以每份数就得到结果。第二种的1份更小，线段也画得更短。

师：1份可以是1，也可以是100，还可能是多少？

生6：1000、10000都可以。

生7：不是整百整千也可以，只要每份是相同的数。

学生说的“1份”就是一个单位，有了这样的铺垫，学生对复杂的问题也能顺利解决。

情境问题：泰国学生小奇来到中国，买了一部价值2000元人民币的手机，这部手机需要多少泰铢？（当时100泰铢兑换人民币23.28元，结果保留整数）

在没有强调“份”之前，笔者对中等能力的学生小高进行访谈，发现他说不清解题过程。小高认为100泰铢为1份，2000元人民币里有多少个100泰铢，显然其思维是混乱的。

学习单位化思想后，小高认为这道题不能把100泰铢作为1份，如图2所示，要把23.28元人民币看成1份，都是人民币才能与2000元人民币具有倍数关系，即2000元里有几个23.28元，就有几个100泰铢。

笔者调查了全班50人，有42人选择以23.28元作为1份进行思考，有8人选择1元人民币换多少泰铢，再算2000元人民币换泰铢的总额。由此可见，单位化思想已经植根在学生心中，使学生分析问题条理清晰，解决问题的能力得到了提高。

五、单位化视角下的结构化学习

在解决问题的过程中，教师要引导学生总结梳理单位化思想，发现不同问题之间的共同特征，形成结构化思维，促进知识的迁移。

比如，如图3所示，两摞同样的纸，第一摞100张，第二摞大约有多少张？教师要引导学生用“份”数思想解决这一类问题，把1.2厘米高的纸看作1份，7.2厘米的纸有这样的几份，就有几个100张。纸的张数不仅可以数出来，还可以通过测量高度算出来。

回顾教材，虽然场景不同，但到处都有单位化思想。比如，一捆铁丝的长度不用靠长度单位测量出来，可以通过称重量算出来；估算体育馆有多少个座位时，可以把场馆进行区域划分，每份差不多，数出其中1份，有这样的几份就能算出大概的座位数。

如图4，估计数量时，同样用到单位化“份”的思想，这成为解决问题的一个重要策略。

在分数除法教学时，如图5所示，教师要以单位化思想引导学生理解分数除法的意义、解释算理、解决实际问题。

马芯兰老师认为，乘除法、倍、比、分数等知识以“份”的概念为核心生长起来，“在教学中，怎么重视‘份’这个概念都不为过”［５］。这里的“份”就是单位化的具体表现，也是理解除法意义的重要手段。

教师以单位化思想为主线，不仅可以提高学生对除法的认识，加深对整数除法、小数除法、分数除法本质的理解，还能让学生串起分数、比、倍等内容与除法的联系，提升学生以结构化思维分析各种现象本质的能力。

参考文献：

［１］［３］ 刘加霞，孙海燕.单位化思想视角下的除法运算本质与教学建议［Ｊ］. 教学与管理，２０２１（２６）：５６－５８.

［２］ 林婕纯. 基于单元整体教学的核心课例研究：以“除法的初步认识”为例［Ｊ］. 小学数学教育，２０２１（Ｚ３）：１７－２０.

［４］ 张奠宙. 教材编写要注意防止片面的思维定式：评小学数学教材中忽视“包含除”的倾向［Ｊ］. 小学教学（数学版），２０１５ （９）：４－６.

［５］ 温寒江. 小学数学教学与创新能力培养：马芯兰教学法的研究与实践［Ｍ］. 北京：北京科学技术出版社，２００６.