以“材”突破难点 用“序”进阶思维

［摘  要］ 研究者以“用字母表示数”一课为例，通过“课前思考，明确单元目标”“课堂实践，彰显代数思维”“教学反思，回顾整体教学”来提炼单元核心目标、重构单元教学序列，尝试以“关系”为主线，发展学生的代数思维。

［关键词］ 代数思维；教学实践；字母表示数；单元视域

一、课前思考，明确单元目标

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）在小学阶段删除了有关方程的内容，移至初中阶段。这样的修订是对小学阶段学生代数思维的削弱吗？笔者从两个方面进行了思考。

1. 如何凸显代数思维，发展学生的符号意识？

新课标将“字母表示数”调整到 “数量关系”主题中，旨在让学生在具体情境中探索用字母表示事物的关系、性质和规律的方法，感悟用字母表示的一般性。

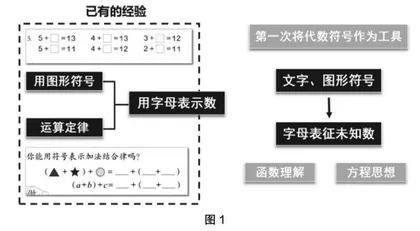
如图1所示，在第一、第二学段中，学生接触过用“图形符号”表示特定的数和用字母表示运算定律，初步积累了用字母表示数的经验。“用字母表示数”单元第一次将代数符号作为工具，让学生经历从文字、图形符号逐步过渡到字母表征未知数的过程，为理解字母表示数的函数和感悟方程思想打下坚实的基础。随着小学教材将“方程”内容移除，“用字母表示数”意在让学生从数量关系的角度来理解“字母表示数”的学科本质，丰富学生对“符号意义”的理解，初步发展学生的代数思维。

2. 如何实现结构化教学，促进学生素养提升？

笔者结合新课标的内容要求、学业要求、教学提示进行系统梳理，明晰“用字母表示数”单元的核心素养表现为符号意识、推理意识和应用意识，并确定本单元的核心目标（如图2所示）。

结合核心素养表现以及核心目标，可以划分出具体的表现性目标（如表1所示）。教师要思考：学生刚刚接触“字母表示数”这个内容的思维瓶颈究竟在哪里？他们面临的“真问题”到底是什么呢？通过学情调查，笔者发现学生主动使用字母表示未知量的意识薄弱，对于字母式表示数存在认知困难，能找出规律却难以抽象出用字母表示的形式。

基于以上分析，从新课标出发，笔者尝试以“关系”为主线进行单元主题架构设想，分成“关系”“性质”和“规律”三个板块，共五个课时（如图3所示）。

第一板块的“关系”建构课，由用字母表示“数”和“关系”两个主题构成，让学生理解字母既可以表示数，也可以表示关系。第二板块的“性质”探究课，让学生学习用字母表示运算定律、公式和性质，强调用字母表示一般化的“数量关系”。第三板块的“规律”主题活动课，让学生对规律进行探究，进而将经验迁移到生活中的其他事物中，从探索生活中复杂的规律到提炼探索一般关系的方法，感悟字母参与运算的价值。

二、课堂实践，彰显代数思维

基于上述分析，笔者围绕单元重构后的关键课例“用字母表示数”进行例证。

1. 回顾百数表，唤醒经验

思考：在一年级的时候，我们已经认识了百数表，百数表里的数字有规律吗？

预设：竖着看，下一行比上一行多10。

预设：也可以横着看，后面的数比前一个数多1。

小结：看来大家对百数表并不陌生，今天我们就借助百数表来进行学习。

2. 借助百数表，直击本质

（1）在猜测中感知

思考：用两个连续的正方形□□去遮住百数表中的两个数，可能会是哪两个数？

预设：可能会是35、36，72、73……

问题：仔细观察，你们发现了什么？

预设：都是相邻的数。

预设：后面的数都比前面的数大1。

追问：除了这几种，还有其他情况吗？

预设：还有很多种可能。

关键问题：这样的情况还有很多，能不能用简明的方式表示被遮住的任意两个相邻的数？

设计意图：教师借助百数表，让学生回顾百数表中上下左右数的关系。在猜一猜的任务驱动下，学生发现每次被遮住的数都是两个相邻数，这样的情况还有很多，如果一种一种表示会很麻烦，需要用一种方式表示所有的情况。这就激发了学生的探究欲望，为感受用字母表示的一般性做好铺垫。

（2）在对比中建构

学生开展关键活动1（如图4所示）。

教师呈现学生作品（如图5所示）。

反馈层次一：

问题：老师收集了这三幅作品，静静观察，你们看懂了吗？

预设：①号只能表示一种情况，不符合要求。

预设：②号表示了一些情况，不是全部。

预设：②号不能表示是相邻的两个数。

预设：③号用字母来表示，字母可以表示很多数，符合要求。

小结：这个方框里的数有很多，是不确定的未知数（板书：未知），未知数可以用字母来表示。

设计意图：教师选取代表具体算术思维和抽象代数思维的学生作品，进行第一层次的对比。在交流中学生发现一个字母可以表示很多数，表示其是一个未知数，初步感知用字母表示数的一般性。

反馈层次二：

思考：如图6所示，也有同学是这样表示的，你们能看懂吗？

预设：前面的数可以用字母a表示，相邻的数比前面要大1，所以就是a+1。

追问：③④两位同学都想到了用a来表示前面的数；对于后面的数，一个是用b来表示的，一个是用a+1来表示的，你们觉得哪一种更合适？

预设：b更加合适，更加简捷。

预设：a+1更加合适，a+1能看出和a的相邻关系，b看不出和a的相邻关系。

预设：字母表中，b就是a后面的数，能看出相邻。

学生在交流中，辨析b和a+1的优势。

（3）在操作中深化

思考：如图7所示，到底哪一种表示方法更合适呢？

①摆一摆

问题：a确定了，b在哪里？a+1在哪里？

（学生上台操作，摆一摆、说一说）

预设：b在a的后面。

预设：b可以在a的后面，也可以在其他的位置，b是自由的。

预设：a+1只能在a的后面。

预设：a+1就表示比a要大1的数。

小结：用b表示，看不出和a的相邻关系，a+1能看到和a的相邻关系。

②移一移

思考：a的位置移动起来，a+1会怎么样？

教师和学生操作互动，教师不断移动a的位置，学生不断找出a+1的位置。

问题：刚才的过程，谁有发现？

预设：a跑到哪里，a+1就跟到哪里。

预设：a+1就是a的“跟屁虫”。

追问：为什么a跑到哪里，a+1就跟到哪里？

预设：a+1就表示比a要大1的数。

预设：不管a怎么跑，它们之间的关系是不变的。

过渡：你发现了不变的地方，那有什么在变化呢？

预设：a和a+1的位置在变化。

预设：a和a+1表示的数在变化。

看来，a变了，a+1也会跟着变化，但是它们之间的关系始终不变。

小结：通过刚才的讨论，我们发现像a、b、a+1这样的字母或者含有字母的式子可以表示数，但是a+1不仅可以表示数，还可以看出和a的相邻关系。（板书）

设计意图：学生通过第二次的对比交流，初步感知a+1的优越性。教师借助空白的百数表，通过摆一摆、移一移，让学生直观发现用b表示的不确定性与a＋1表示的确定性，理解两个变量之间变与不变的关系。通过百数表中一个框代表一个数，让学生潜移默化地突破含有字母的式子既能表示数、又可以反应两个量之间的关系这一难点。

反馈层次三：

问题：如图8所示，还有同学是这样表示的（出示⑤号），你们能看懂吗？

预设：先确定后面的数，前面的数就是a-1。

预设：这两个数是相邻的两个数。

思考：如图9所示，比一比，你有什么发现？

预设：④和⑤都表示相邻的两个数。

预设：它们的标准不一样，一个是用前面的数作为标准，一个是用后面的数作为标准。

小结：看来，选择的标准不同，表示的字母式也不同，但是它们的关系是不变的。

设计意图：经过第三层次的对比，进一步深化学生对字母表示两个变量的理解。在表示的过程中，选择的变量不同，表示的方式也不同，但都表示两个量之间的相邻关系，为学生后续学习用方程设不同的未知量做好准备。

（4）在辨析中完善

问题：想一想，对于④和⑤两种情况，a可以是哪些数？

预设：a可以是任何数。

预设：a可以是1～100的整数。

预设：用④来表示，a不可以是整十数。

问题：你能上来一边摆一边说吗？

预设：如果a是整十数，那么a+1就跑到百数表外面去了。

预设：用⑤来表示，a的个位不能是1，不能是第一列的数。

问题：看来，某些情况下，字母表示数是有范围的。（板书）

问题：尝试代入求值，a=25时，a+1=25+1=26。其他情况会求吗？

设计意图：在讨论、想象和辨析的过程中，学生感受到用字母表示数，在具体的情况下是有一定的范围的，并且字母和字母式中的数可以参与运算，进一步完善了用字母表示“数”的内涵。

（5）在创造中巩固

思考：如图10所示，现在a的下面有一个方框，这里的数会是几呢？

预设：a+10，从百数表里竖着看，下一行的数比上一行的数多10。

如图11所示，学生开展关键活动2：现在还有一个方框，这个方框可以放在哪个位置，方框里的数会是几呢？

教师呈现学生的作品（如图12所示）。

预设：放在④号位置，用a-1来表示。

预设：放在②号位置，用a-10来表示。

预设：放在⑦号位置，用a+11来表示。

预设：也放在⑦号位置，我用a+1+10来表示。

追问：都是⑦号位置，怎么会有两种答案呢？

预设：a+11和a+1+10是相等的，里面的1+10就是11。

小结：看来字母式中的数可以参与运算。

问题：如图13所示，如果把中间的3个数圈起来，你们能求出它们的和吗？

预设：a-1+a+a+1=a+a+a。

预设：a×3。

设计意图：根据百数表中上下左右方框之间的数量关系，教师借助“一个方框可以放哪里”的任务驱动，让学生经历想象与创造的思维过程。在游戏化的学习过程中，学生不断深化理解含有字母的式子既可以表示数，又能表示两个量之间关系，无痕过渡到对用字母表示乘法的数量关系的理解。

3. 跳出百数表，走向生活

思考：a×3表示百数表中连续3个数的和。如果跳出百数表，a×3在生活中还能表示哪些情况呢？

如图14所示，这些情况能用a×3表示吗？如果可以，请连一连；如果不可以，请写出正确的字母式。

追问：③和④为什么不能连呢？

预设：③知道总价求单价，应该是a÷3。

预设：④应该是a×3+3。

追问：除了这些情况，生活中还有哪些情况可以用a×3表示？

预设：长方形的长是3，宽是a，面积是a×3。