结构化视域下单元整体教学的实践探索

［摘  要］ 文章以“有余数的除法”复习教学为例，基于“结构化”的设计思想，从“梳理旧知，整理巩固”“闯关练习，实际应用”“思维导图，构建体系”三个环节开展教学设计与分析，研究小学数学课堂中单元整体教学的可行性，为发展学生核心素养奠定基础。

［关键词］ 结构化；单元整体；教学

《义务教育数学课程标准（2022年版）》强调数学教学要将知识纳入整体结构中，基于整体视域设计教学活动，这对促进学生的发展具有重要价值。然而，仍有部分教师习惯以课时教学为主，导致学生对知识的掌握存在碎片化的情况，无法抵达深度学习。为此，笔者基于结构化视域对单元整体教学开展实践与探索，以期优化教学。

一、教学设计思想

数学是一门系统性的学科，教师要基于整体的视域设计教学方案，让学生感知数学学科的系统性，避免形成孤立无序的知识结构。为了实现这一目标，教师在设计教学方案时要灵活应用教学方法，让每个认知水平层次的学生都能各扬所长，在课堂中获得不同程度的发展。在教学过程中教师要充分体现“生本”理念，让学生基于自主思考、合作交流、及时反思等模式主动接纳教学内容。从教学评价的维度来看，教师在结构化视域下单元整体教学时，要多维度、多元化、综合性地评价教学过程。

二、设定教学目标

教学目标是教学的方向，课前教师要结合学生的实际认知水平与教学内容特点设定教学目标。尤其是复习课教学时，教师要关注知识的整体性特征，为优化学生的数学思维建构结构化的知识体系服务。“有余数的除法”的教学目标主要有：①借助思维导图揭示“有余数的除法”的竖式写法、读法等，进一步巩固学生对除法竖式中各个数的理解，为形成结构化思维做好铺垫；②借助闯关法实施练习训练，让学生对除数与余数间的关系产生明确认识；③让学生用所学知识解决实际问题，进一步感悟“有余数的除法”的实际应用。

三、教学过程设计

1. 梳理旧知，整理巩固

师：在之前的学习中，大家已经接触过“有余数的除法”这部分内容，现在请大家组内交流，说说自己已经掌握了哪些与“有余数的除法”相关的知识？

生1：关于“有余数的除法”算式，我会读，也会写。

师：请你到讲台上给大家展示一个有余数的除法算式，并规范地读出来。

生2：我还知道在这一类式子中，余数都比除数小。

师：很好！现在来看这个情境——小明有15个梨，准备将这些梨平均放到4个水果盘内。大家以此为例，说说为什么余数小于除数？

生3：将15个梨平均放到4个果盘内，列式为15÷4；如果一个一个地放，当每个果盘内放1个梨时，剩下11个梨，11＞4，需要继续分；当每个果盘内有2个梨时，还剩下7个梨，7＞4，需要继续分；如果每个果盘内有3个梨，剩下3个梨，3＜4，此时不够分。

总结：除法算式中，如果余数大于除数，则具备继续分的条件；如果余数小于除数，则不再具备继续分的条件，由此可确定在除法算式中，余数都比除数小。

师：有余数的除法竖式该怎么列式？

教师引导学生一起规范书写有余数的除法竖式，总结计算过程中的“除”“乘”“减”，并强调商与被除数数位对齐的要求。完成之后，教师鼓励学生自主总结提炼，为厘清复习思路以及灵活应用相应的知识做好铺垫。

设计意图：复习教学环节，在教师的引导下，学生对旧知进行回顾与梳理，并鼓励学生自主应用思维导图的方式整理知识点，起到再次回顾、总结与巩固的作用。

2. 闯关练习，实际应用

（1）分析除数、被除数、商以及余数间的联系

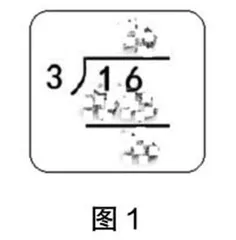
教师用多媒体展示竖式（见图1），竖式的商和余数均显示不清，要求学生根据已有的认知经验，猜想该竖式的商和余数分别是什么，并说明理由。

学生讨论，一致认为商为5，余数为1。理由为：如果商为4，那么该竖式的余数就是16-4×3=4，余数4＞除数3，不合理。如果商为6，那么6×3=18，而18又大于被除数16，也不合理。由此可确定，本题的商必然为5，余数只能是1。

师：观察图2，其中显示不清的除数是什么数？

学生考虑到“除数×4”能让个位数出现8的情况，只有除数为7才行，因此确定7为本竖式中的除数。

设计意图：显示不清的竖式，让学生学会从不同维度来思考竖式中的各个数，如此设计可训练学生分析问题的能力，让学生学会根据已知条件反推出除法计算中的商、除数等［１］。此为发展学生推理意识、数学运算等素养的过程，能进一步强化学生对算法、算理的理解。

（2）探索“整除”与“有余数的除法”的联系

教师要求学生观察四个算式：①42÷7；②26÷4；③32÷5；④16÷4，并按照“算式结果是否存在余数”进行分类，说说快速判断的方法。

学生通过观察，用乘法口诀进行快速判断，一致认为可将①④归为整除，②③归为有余数的除法。

师：接下来，大家一起来观察□4÷2、□3÷5两个式子，这两个式子被除数的十位数均不明确，该怎样判断这两个式子的计算结果是否有余数呢？

生4：第一个式子的除数为2，被除数个位上的数为4，不论十位上的数为几，这个被除数均为双数，任何双数除以2均为整除，故不会出现余数。

师：分析得很好，第二个式子呢？

生5：以前我们学过5的乘法口诀，有5、10、15、20、25等，即任何数与5相乘，个位只能是0和5。问题中的被除数个位数为3，因此该式除以5必然无法除尽，存在余数。

设计意图：两个缺失十位数的算式，成功激活了学生的思维。如此设计不仅进一步巩固了学生乘法口诀在有余数除法中的应用，还促使学生学会通过分析问题，主动进行知识的建构，形成良好的解题能力。通过两个算式的探索与交流，能让学生切身体会有余数的除法与原本学过的乘除运算有内在关联，感知数学知识的系统性特征。

（3）借助有余数的除法解决实际问题

问题1：小红有一串漂亮的彩色串珠手链，手链分别由红、黄、蓝、绿四种颜色的珠子依次串联，如果手链上的红色珠子数量为4，那么这串手链一共有多少颗珠子？

师：请大家先画图，再分析问题，用列式计算法解决问题。

生6：手串中存在4颗绿色的珠子，根据手串的组合，可认为串珠的总数量为4×4＝16（颗）。

生4：万一串联了4个组合之后，后面又增加了1颗红色珠子呢，在这种情况下，可列式为4×4+1=17（颗）。

生7：按照这种理解，在串联了4个组合之后，后面还有可能增加“红+黄”或“红+黄+蓝”，即增加2颗或3颗珠子，分别列式为4×4+2=18（颗），4×4+3=19（颗）。

师：有没有可能在串联了4个组合后，再增加4个珠子？

生8：不可能，因为题设条件中已经明确只有4颗红色珠子，如果增加4颗珠子，那就出现了5颗红色的珠子。由此可获得本题的结论可能为16、17、18、19颗珠子。

设计意图：此为“有余数的除法”应用到生活中解决实际问题的过程，解决问题的本质是“余数＜除数”。通过对实际问题的分析与思考，学生发现除法的核心为物品的平均分配问题，在剩余数量小于份数的情况下，剩余数量则为余数。教师如此设计，意在进一步强化学生对余数必定小于除数的认识。

（4）“进一法”与“去尾法”的应用

科技活动中，学生准备自制一些纸船帮助玩具过河。已知制作1条纸船需耗费3张纸板，1条纸船限装5个玩具。

问题1：20张纸板可以制作几条船？

生9：20÷3=6……2，可制作6条纸船。

师：说说你的理由。

生9：因为1条船要耗费3张纸板，当做完6条纸船时，就剩下2张纸板，不够再做1条纸船。因此，20张纸板只能制作出6条纸船，剩下2张纸板无法利用。

师：不错，这就是我们数学中常用的“去尾法”。

问题2：现有23个玩具，如果想让它们全都渡过河，最少要制作几条船？

生10：列式为23÷5=4……3，确定需要5条船才能将这些玩具一次性渡过河。

师：5条船的理由是什么？

生11：如果制作4条船，那么能运走的玩具数量为4×5=20（个），这样就有3个玩具无法过河，只有增加1条船才能一次性将这些玩具都运到河对面去。

师：这就是数学中的“进一法”。

问题3：如果我们班有17个玩具，隔壁班有23个玩具，两个班合作，至少需要制作多少条船才能将这些玩具一次性运到河对面？

生12：考虑到两个班合作，可将玩具放在一起，列式为17+23=40（个），40÷5=8，即制作8条船可完成任务。

设计意图：此问意在考查学生灵活应用数学知识解决生活实际问题的能力，让学生获得具体问题具体对待的思想，同时渗透“去尾法”与“进一法”，不断提升学生的应用意识。

3. 思维导图，构建体系

教师要求学生自主梳理有余数的除法相关知识结构，并将相应的内容以思维导图的形式呈现。学生自主整理与总结，形成知识结构图（如图3）。

设计意图：思维导图的制作可进一步完善学生的认知结构，让学生在知识的梳理与总结中发展数学逻辑思维，获得探索与分析数学问题的基本能力。

四、教学思考

1. 关联生活，获得数学眼光

核心素养导向下的课堂教学要关注学生“三会”能力的培养；结构化视域下的单元整体教学同样要培养学生用数学的眼光观察世界的能力［２］。本节课为复习教学，学生对有余数的除法已经有一定的经验基础，因此教师在设计教学活动时，可关联学生的生活实际，引导学生学会抽象生活现象，获得用数学知识解决生活问题的基本能力。纵观本节课，从课堂伊始的梨子分配问题到手串问题，再到制作船运玩具的趣味问题，都与学生的生活实际相关联，让学生在潜移默化中形成用数学的眼光观察世界的能力。

2. 关联知识，完善知识结构

复习教学与课时教学最根本的区别在于，复习教学将零碎的知识串联重构，可进一步完善学生的知识架构，让学生对教学内容形成系统化的认识。课时教学受到很多限制，教师授课时要关注知识重点与难点的突破，导致学生在新知的建构上难免会厚此薄彼。复习教学在学生已有认知经验基础上进行，教师要注重知识的关联，厘清知识内部结构与联系，让学生形成完整的知识体系。本节课，学生就在教师的引导下，将零散的知识聚合到一起，用完整的思维导图呈现知识体系，凸显了结构化思维与整体性教学的优势。

总之，新课标引领下的数学教学，要以学科知识为基础，以知识结构为载体，联系学生的生活实际设计问题，逐步发散与拓展学生的思维，让学生自主形成用数学的眼光、数学的思维与数学的语言去观察、思考与表达世界的能力。

参考文献：

［１］ 董欲爽. 串点成线，巧编知识网：“有余数的除法单元复习课”教学设计［Ｊ］. 小学数学教师，２０２１（１２）：５４－５７.

［２］ 丁科州. 小学数学“图形与几何”大单元教学实践策略研究：以人教版六年级上册为例［Ｄ］. 银川：宁夏大学，２０２２.