大单元视域下问题引领小学数学教学的探索

［摘  要］ 文章阐述了问题引领教学的内涵、模型，并以“比的认识”的教学为例，从情境引发问题、分类整理问题、衍生新的问题、回应其他问题、分享问题积累经验等方面进行探索与研究。

［关键词］ 问题；大单元；情境教学

《义务教育数学课程标准（2022年版）》倡导教师应引导并鼓励学生积极主动参与课堂教学活动。教师基于大单元视域，以“问题”为线索，通过问题揭示教学内容，不仅能激活学生的思维，提高学生的课堂参与度，还能引发学生的探究意识，培育学生的创新思维。

一、问题引领教学的内涵

以问题引领教学是指教师基于真实的情境开展教学活动，把引导学生自主发现与提出问题作为初步教学任务，把引导学生自主分析并解决问题作为教学目标，以此激发学生的学习动机与自信，发展学生“四能”，从情境中培养学生“三会”的能力。

问题引领教学的内涵主要表现在三个方面：①让学生学会从情境中发现并提出问题；②让学生持续不断地发现问题并解决问题，以此作为促进学生持续发展的动力；③“学问交融”，即让学生经历不断重复发现、提出、分析与解决问题的过程，让问题伴随学生学习的全过程［１］。

二、问题引领教学的模型

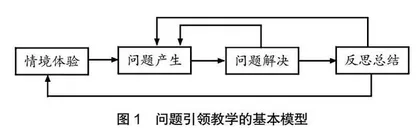
利用问题引领教学的本质是真实还原学生的学习过程。部分教师只是为了完成教学任务而设计问题，学生缺乏自主发现问题并提出问题的机会。这种将问题“喂”给学生的教学模式，不是真的“问题引领教学”，实则为流于形式的“程式化教学”。因此，教师应灵活变通教学模式，用各种方式最大化地发挥问题的作用。如图1所示，在不同形式与时长下，问题引领教学的方式可以灵活变动。

图1揭示了问题引领教学的基本流程，值得关注的是，由情境引发问题仅是开始，在问题解决与反思总结阶段都能产生新的问题，正是这种不断产生问题与解决问题的教学过程发展了学生的思维。

三、问题引领教学实践

1. 情境引发问题

数学知识是由现实生活中的真实事物抽象而来，解决生活实际问题是数学知识存在的主要作用。教师在课堂中创设丰富的教学情境，能有效激起学生的兴趣。新颖、复杂、具有显著冲突性的情境能引发学生的认知冲突，吸引学生开展探究。在教学“比的认识”时，教师可以结合学生的生活经验创设情境，引导学生感知怎样运用两个数量的比来处理问题。

（1）情境创设

情境：展示图2，要求学生观察图中哪两幅图具有相像性，并分析其长与宽的比。

为了深化学生的理解，揭示“像”与“不像”的本质，促使学生从真正意义上理解“比”的意义，教师课前布置了一个“照片拉伸”的任务，要求学生在课前自主完成：利用计算机软件处理图片，借助“拉伸”功能调整图片的大小，看看拉伸过程中会出现什么情况，并将操作过程中的情况与感悟记录下来（见表1），为经验交流作准备。

学生通过自主操作、观察、记录，直观感知图形在拉伸过程中产生的变化，发现图形的变化与其长、宽的改变相关，由此充分感知探索“比”的必要性。

（2）提出问题

随着以上情境的探索，学生不仅获得丰富的体验，还自然地提出了很多有趣的问题。从搜集的问题来看，大部分问题都是围绕图形拉伸前后的关系提出的，也有少数问题与比有关，比较典型的问题有：①如何调整照片的长、宽，使原图的外观不会发生变形？②有什么办法让图片与原图高度相似？③为什么经拉伸后的图片大小不同，视觉效果却一样？是因为拉伸前后的长、宽的比是一样的吗？④为什么从上下或左右拉伸后，图片会变形？⑤如果将长、宽拉长或减少的长度一样，图片会发生变形吗？

以上问题都是围绕图片的拉伸提出的，也有不少学生提出其他问题，如鼠标技术、图片处理器、A4纸的长宽、黄金分割等问题。

从学生提出的问题来看，恰当的情境不仅可以将学生的目光聚集到相应的探索内容上，还能突破学生思维定式，促使学生从不同的角度来思考同一现象，这对发展学生的创新意识具有重要意义。

2. 分类整理问题

学生所提出的问题多且杂，课堂上教师不需要将所有问题都讲一遍，最好的办法就是将这些问题按照一定的逻辑进行梳理，形成问题链，为学生的单元学习提供方向，这是促进学生阅读与理解问题的过程。

具体操作方法为：首先，学生通过阅读问题，将不理解与最想解决的问题提取出来；然后，师生共同探讨，去掉一些重复的问题，将剩下的问题以一定的标准进行分类；最后，选取具有代表性的问题在课堂上共同交流。

学生经过交流与提炼，将问题分成三类：第一类，拉伸前和拉伸后的图形像不像，如何调整图形的长与宽，使之不变形等；第二类，与“比”相关，如黄金分割的概念、确定A4纸长与宽的方法等；第三类，与技术相关，软件能否实现拉伸后让图形不发生变形。

将问题分类之后，教师要鼓励学生从每一类问题中挑选一些问题进行讨论与分析。比如，有的学生选择第一类问题“如何调整图形的长与宽，让图形不会发生变形”，随着这个问题的探索与解决，学生发现这一类问题中的其他问题都能顺利解决。据此，单元的学习方向与路径基本确定，当学生在探索本单元其他内容时也可以采取这种模式促进深度学习的发生。

3. 在解决问题中再提出新的问题

关于“如何调整图形的长与宽，让图形不发生变形”这个问题，教师借助情境中的图引导学生自主分析与探索。

如图3所示，不少学生认为，与原图相比，图3中①和③只是图片大小发生了变化，图片并没有变形，②明显变形了；有的学生提出反对意见，因为仅凭借肉眼无法判断图片是否变形。由此，学生衍生出一个新的问题：“用什么办法来确定图形是否变形了？”

随着新的问题的提出，学生进行了交流。

生1：将原图和其他三幅图片剪下，进行折叠、测量可确定：图3中②的长宽与原图的长宽不是倍数关系，①③的长宽与原图的长宽为1.5倍的关系。

生2：其实我们可以将这些图放到图2中的方格纸上，这样就能快速看出图片长宽的倍数。

师：这个方法不错，现在请大家用方格纸分别测量几幅图的长宽，比较每一幅图的长宽倍数。

由此获得结论，即想要让原图不发生变形，就要按照一定的比例拉伸原图的长宽。“比”的概念在这个结论中诞生。

随着“比”的概念的形成，学生将概念延伸到生活中，探索实际生活中与“比”相关的情境。

实践发现，“学问交融”是问题引领教学的重要策略之一。学生在对问题的探索中不断发现并解决新的问题，并应用所获得的结论来解决实际问题，不断提升自身的“四基”与“四能”。当学完“比”的概念后，学生产生了新的问题：如果图3中的①③由原图拉伸而来，那么这三幅图的长宽比一定相同吗？为了探索这个问题，学生借助信息技术将图形粘贴到方格纸上进行观察，并记录，获得表2。

探索每幅图拉伸后的长宽比与原来的长宽比的关系，发现化简后的比值一样。由此，学生自然形成了问题：“任意图形的长宽比都需要化简吗？‘比’适用‘商不变’的规律吗？”

从教学流程来看，随着“比”的概念的抽象，通过问题的提出与解决，学生自然地过渡到新的探索主题“比的化简”［２］。此过程凸显了单元整体教学的优势，使学生的思维经历由浅入深的变化过程，逐渐搭建出完整的知识架构。

课堂尾声，有的学生提出问题：“‘比’与‘比的化简’具体应用在生活的哪些方面呢？”

显然，这个问题涉及后续探索的“比的应用”。由此可见，问题的形成与解决是一个不断循环、向前推进的过程，因为有问题的引领，学生的思维才能拾级而上。

4. 回应其他问题

问题推动了教学的进展，促使深度学习的发生与学生思维的发展。本节课的问题主要由学生自主提出，取得的教学成效非常明显。教师该怎样处理学生提出来的与课堂教学内容无关的问题呢？此为值得重视的问题。

为了回应学生在本节课所提出的与教学内容关系不大的问题，教师可以设计一个“问题角”，将课堂上无法解决或难度较大的问题打印出来展示在教室的某个区域，比如学生提出的“怎样确定A4纸长与宽”的问题，为教学留下悬念。如图4所示，“问题角”的应用可以遵循这个流程。

这种方式不仅尊重了学生，重视学生所提出的每一个问题，还在无形中提升了学生思考的时间与空间，增强了学生的学习自信。教师要从真正意义上促进学生的可持续发展，要尊重学生的个体差异，为学生提供充足的时间与空间，鼓励学生自主探索与研究。

5. 分享问题积累经验

单元教学结束时，教师可以有针对性地安排一个问题交流时间，让学生将自己在学习过程中所获得的发现与解决问题的经验展示出来。比如，教师先要求学生回顾自己所提出的问题，将自己觉得最满意的那个问题展示出来；然后，让学生选出最喜欢的问题进行投票，将得票率最高的问题选出来；最后，让提出这个问题的学生说明问题背景与提出缘由。

随着活动的开展，学生不仅可以选出自己最喜欢的问题，还可以修改完善自己提出的问题，分析总结提问的经验。

总之，在单元教学中，教师应用“问题引领教学”模式可以揭示知识的本质，将零散的知识点串在一起形成结构清晰的知识体系，促使学生在问题的形成与解决中不断产生新的问题，并在新的问题的解决中逐步提升与发展能力。

参考文献：

［１］ 张丹. “问题引领学习”：让儿童学习走向深入［Ｊ］. 中小学管理，２０１７ （６）：４１－４４.

［２］ 史宁中，娜仁格日乐. 小学数学教科书中的比及其教学［Ｊ］. 数学教育学报，２０１７，２６（４）：１－５.