简便运算错误归因及对策探析

［摘  要］ 研究者对学生的乘法简便运算错误归因进行分析，抓住乘法分配律的本质特征进行教学，帮助学生巩固乘法分配律，促进学生形成知识体系。

［关键词］ 小学数学；简便运算；知识体系；对策探析

运算是数学的基本研究对象，也是数学的一种基本思维形式。运算能力主要包括能够根据运算律、运算法则和运算程序熟练进行四则运算。在小学数学教学中，简便运算的教学是培养学生运算能力不可或缺的一部分，不仅可以渗透化繁为简的思想，提高学生的运算能力，还可以提升学生的数学思维品质，促进学生高阶思维能力的发展。

一、简便运算的错误成因及现状

在简便运算中，对运算定律本质的理解是学生灵活进行简便运算的关键。对学生来说，最难掌握的运算定律是乘法分配律，学生在运用时常常出现错误，容易与乘法结合律混淆。究其原因主要是乘法分配律的模型与其他运算定律的模型不同，学生难以理解，尤其是学生学习了小数和分数乘除法后遇到的简便运算类型繁多。因此，教师要引导学生掌握简便运算的技巧和方法。

现行的小学数学统编教材第二学段运算定律内容包括加法交换律和结合律、乘法交换律和结合律以及乘法分配律，要求学生能用字母表示运算律，并理解算理和掌握算法，培养代数思维；第三学段运算教学的主要内容包括简单的小数、分数四则运算和混合运算，重点是让学生感悟运算的一致性。因此，在第三学段学生学习了小数和分数的运算后，教师要对学生的乘法分配律运用能力进行检测和错误归因，并通过结构化设计“乘法分配律再认识”的教学活动，帮助学生深入理解乘法分配律的本质特征，巩固乘法分配律的应用，牢固架构乘法分配律的模型，促进学生形成知识体系，提升学生的运算能力和高阶思维能力。

二、简便运算的有效策略

简便运算在小学数学教学中具有重要地位，它不仅能提高学生的计算速度和准确性，还能激发学生学习数学的兴趣，培养他们的思维能力和创新精神。

1. 检测练习，铺垫精准施教

当学生学完第二学段的探索运算定律之后，教师要在第三学段的小数乘除法四则运算中继续探索运算定律对于小数是否适用。教学中，笔者发现学生在简便运算中乘法分配律的应用错误较多。因此，在教学整数乘法运算定律推广到小数后，教师要利用习题进行检测，帮助学生寻找产生错误的原因及对策。

师：同学们，小数乘除法的学习已经结束，下面挑战“计算小能手”的时刻到了。现在老师给出12个题目，请你们快速进行简便运算。

①472×78＋528×78；②（1.25－0.125）×8；③1.25×2.5×32；④7.6×102；⑤65×101－65；⑥9.8－9.8×0.7；⑦10.6×5.09－0.6×5.09；⑧44×250；⑨6.8×3.8＋38×0.32；⑩36.5×9.9＋3.65；？輥？輯？訛7.2×0.4+2.4×4.8；？輥？輰？訛98×7.2+14.4。

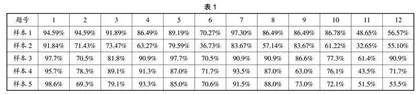
运算结束后，通过数据的收集和统计，笔者发现学生错误较多的地方集中在变式练习。部分学生直接运用四则运算，虽然结果正确，但是方法不简便。为了收集更多的第一手资料，以便进一步了解学生的运算错误原因，笔者对本校其他班级进行了抽样比对，并对所抽测班级的学生进行访谈，发现学生在运算时遇到的困难很多，正确率见表1。

（1）学生对乘法分配律的基本模型掌握不牢固，容易在分与合的过程中出错，比如出现（1.25－0.125）×8=1.25-0.125×8或1.25×8-0.125的错误。

（2）学生对乘法分配律和乘法结合律出现混用，比如出现1.25×2.5×32=1.25×8+2.5×4，7.6×102=7.6×100×2，44×250=40×250×4或者40+4×250等错误。

（3）在变式练习中运用乘法分配律时出现错误。部分简便运算的题目在不改变运算结果的情况下，需要学生创造条件找到适合乘法分配律的模型进行运算，但是有的学生无法创设出与运算结果一致的乘法分配律模型。比如出现44×250=40+4×250，36.5×9.9＋3.65=3.65×（9.9＋0.1）；7.2×0.4+2.4×4.8=7.2×（2.4-0.4）×4.8；98×7.2+14.4=98×7.2+（14.4÷2）等错误。

精准定位学情是教师进行教学思考与实践的前提，通过检测，对学生的错误进行归因，能为下一步的精准施教做好铺垫。

2. 课堂实施，探究解决方法

笔者通过检测摸清了学生在简便运算过程中的错误类型，找到了乘法分配律应用错误的根本原因，即学生对本质模型理解不到位，无法创造符合乘法分配律模型的简便运算方法。因此，笔者通过三个教学活动串联本节课，帮助学生加深对乘法分配律模型的本质理解。

活动一：快速完成解答（限时4分钟）。

①笔算：14×12。

②简算：3.5×9+3.5。

③如图1所示，求长方形的周长。

④如图2所示，求组合图形的面积。

⑤妈妈到超市买了4千克的苹果，每千克7.5元，又买了同样价格的梨子8千克，妈妈一共花了多少钱？

东北师范大学史宁中教授认为，模型是数学发展所依赖的思想本质之一。因此，理解乘法分配律模型有助于学生理解乘法分配律概念的本质，为灵活简便运算打下坚实的基础。教学伊始，在学生快速完成解答后，教师应激活学生原有的知识经验，促使学生在挑战练习的过程中逐渐形成乘法分配律的模型意识，进而掌握乘法分配律的定义和字母公式，凸显乘法分配律的本质特征。

活动二：引导学生对熟悉的教材内容进行梳理，寻找教材中乘法分配律的模型，在归纳与提炼的过程中系统认知乘法分配律，并形成乘法分配律的结构化知识链（具体见表2）。

通过梳理教材可知，乘法分配律的模型分布较广，涵盖小学的各个年级。教师要引导学生对熟悉的数学问题进行简化和抽象概括，且重视梳理与提炼，以实现对乘法分配律的结构化认知。在知识模块上，教师要从简单到复杂、从低年级到高年级，一步一步地引导学生梳理其中的乘法分配律模型a（b±c）=ab±ac或（a±b）c=ac±bc，让学生整体感知整数、小数、分数在乘法分配律中的运用，真正理解乘法分配律以及如何简便计算整数、小数和分数的四则混合运算。教师要引导学生将已经学过的与即将学习的乘法分配律内容整合在一起，构建一个完整的知识体系。在这一过程中，教师引导学生进一步体会乘法分配律的本质特征，培养学生乘法分配律的模型意识。

活动三：不用计算，哪些题目可以运用乘法分配律进行简算？

①21×9＋19×9；②4.2×7.5+7.5×5.8；③3/5×2+2/5×2；④9.8－9.8×0.7；⑤（1.25－0.125）×8；⑥0.65×102；⑦98×7.2+14.4；⑧1.25×2.5×32；⑨44×250。

首先，教师引导学生观察数据，让学生直观寻找算式中含有乘法分配律的模型a（b±c）=ab±ac或（a±b）c=ac±bc，即含有两级运算的乘法是否有一个因数是相同的，另外两个因数是否可以凑整进行简便运算。比如：21×9＋19×9，4.2×7.5+7.5×5.8，3/5×2+2/5×2，（1.25－0.125）×8。

其次，让学生观察符号。观察符号和观察数据同等重要，能让学生懂得必须明确乘法分配律的本质特征才能真正进行简便运算。乘法分配律的模型包含着两级运算符号形式，教师要引导学生寻找乘法分配律的模型，判断题目是否具有乘法分配律的模型。

再次，让学生创造条件。当算式中无法直接看出乘法分配律模型时，学生可以在不改变运算结果的情况下，创造符合乘法分配律的模型进行简便运算。比如，9.8－9.8×0.7中有相同的因数，但是缺少一个相减的因数，此时可创造条件9.8×1－9.8×0.7，使其符合乘法分配律模型。这样的创造需要学生以模型为基础，充分思考符合要求的条件进行创造，并借助乘法分配律对运算过程进行重组和化简，得到不同的算法，提升自身的思维品质。

活动中，学生对于0.65×102、98×7.2+14.4、1.25×2.5×32、44×250这四个题目都能通过创造条件，重组与乘法分配律模型一致的简便运算。但是在1.25×2.5×32这一题中，学生还是会经常出现创造错误的条件，如1.25×8+2.5×4，这说明其没有掌握乘法分配律的本质，将乘法分配律与乘法结合律混淆。因此，突破这一难点的关键是教师要让学生理解运算律的本质，在仔细观察数据时注意观察符号，树立乘法分配律的模型意识。

最后，让学生优化简算。在44×250中，学生能够创造条件进行简便运算，如4×11×250和（40+4）×250=40×250+4×250，两种形式一个是运用乘法结合律简算，另一个是运用乘法分配律进行简算，通过多种对比，从中找到最优的简便运算方法。

活动三中层层深入的问题设计，旨在让学生经历“观察数据—观察符号—创造条件—优化简算的运算策略中逐一体验乘法分配律模型”的过程，提升运算能力，发展高阶思维。

3. 回顾反思，提升数学素养

（1）在活动中抓本质——识模

学生的认知结构在掌握知识的过程中形成和发展，是其原有认知结构与新知识相互作用的结果。教师要引导学生在活动中建立乘法分配律的模型，通过激活学生原有的知识经验，增强学生对乘法分配律概念本质的理解，形成乘法分配律的知识链，体会乘法分配律应用的灵活性。在强化乘法分配律原型认识的变式练习中，教师要通过生生互学、思辨讨论，让学生形成一定的方法和策略，从而使学生的认知结构达到新的高度与深度。

（2）在梳理中重结构——固模

在单元整体教学设计时，教师可能会较多地立足一个单元的设计，较少从纵横交错的教材中思考。学生对于乘法分配律并不陌生，虽然到四年级才正式学习，到五、六年级进行深度学习，但学生脑海中存在的都是点状的认知。本节课的活动二是梳理教材中的乘法分配律模型，关联了整个小学的阶段，甚至包括初中阶段的猜想，从不同的角度给了学生不一样的思路。教师要从不同的视角巧妙设计乘法分配律的学习活动，让学生将乘法分配律连点成线，加深对乘法分配律的再认识，促进对乘法分配律知识体系的架构和固模。

（3）在思辨中成系统——用模

课堂要以学为中心进行变革，变的不仅有教师的教学方式，还有学生的学习方法。比如在活动三中，教师不仅引导学生去观察数据、观察符号、结构性创造条件，掌握乘法分配律的应用，还引导学生对乘法分配律进行深入探究，并体会方法的多样性，强化对乘法分配律的建模和用模。

三、结语

乘法分配律的应用是运算定律教学中学生容易出现“反复性错误”的内容。教师要引导学生建立乘法分配律的基本模型，加深学生对乘法分配律概念本质的理解，并以乘法分配律的本质模型为关键点，让学生在经历梳理教材、变式练习中加深对概念本质的理解，形成对概念的基本认知。教师要引导学生在归纳与提炼的过程中实现概念的结构化，形成乘法分配律的知识链；让学生在梳理解题思路中获得简便运算的方法与策略，从而培养学生数感，促进学生形成知识体系。