基于“深度学习”的数学高阶思维培养策略

［摘  要］ 研究者以“负数的初步认识”的教学为例，提出基于“深度学习”理念，培养学生数学高阶思维的教学策略：聚焦学情，真实体验是培养高阶思维的前提；巧妙设问，引发探究是培养高阶思维的源泉；学会等待，充分“让学”是培养高阶思维的关键。

［关键词］ 深度学习；高阶思维；负数

教师要以“核心问题”引导小学生进行数学深度学习，从而培养其数学高阶思维能力。那么，教师要怎样基于“深度学习”理念培养小学生的数学高阶思维能力呢？笔者以“负数的初步认识”的教学为例进行阐述，以供参考。

一、高阶思维能力的实践

1. 教学环节1：抛出问题，激活思维

问题1：大家课前“找负数”的任务完成得怎样？请分享自己的成果。

学生踊跃回答，比如电梯里的负数、天气预报播报中的负数、股票市盈率的负数等。

问题2：显然，负数与日常生活息息相关，你们想知道哪些有关负数的知识呢？

学生开动脑筋，提出问题：负数究竟表示什么？什么情况下用负数表示？负数该怎么读和写？负数是如何产生的？

设计意图：问题是引发学生思维的动力。这里，在课堂导入环节，教师以“上位概念”为背景，以问题为载体，引导学生认识和了解生活中的负数，并促使他们自然深入地思考负数。学生通过对问题的深度思考，逐步明晰探究方向，并为后续的深度探究做足准备。

2. 教学环节2：渐深探究，发散思维

问题3：《九章算术》中记载“粮食入仓为正”，“入仓为正”是什么意思，你知道吗？出仓粮食的数量该如何表示呢？

学生发挥想象，认为粮食进入仓库就是“入仓”，“入仓为正”就是入仓粮食的数量记为正数。同理，出仓粮食的数量就记作负数，即“出仓为负”。

问题4：1700多年前，中国数学家刘徽提出正数、负数的概念；400多年前，法国数学家吉拉尔首次用“+”表示正数、“-”表示负数。比如，“入仓35石”可记作“＋35石”，那么“出仓15石”该如何表示呢？（－15石）

设计意图：融入负数的发展史，让学生感知负数的背景和发展进程，自然地引出负数的概念。更重要的是，通过巧妙揭示负数的数学本质能促进学生对其意义的正确理解。

问题5：组内分享收集的负数例子，并思考这些负数表示的意思。

学生在组内讨论后出现了几种想法。

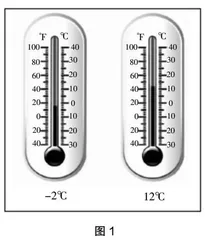
想法1（关于温度）：2023年1月20日某市最高气温是12℃，最低气温是-2℃，这里的12℃表示的是零上12℃，-2℃表示的是零下2℃。从温度计上来看，如图1所示，-2℃就是从0℃往下数2小格，而12℃就是从0℃往上数12小格。温度计上，虽然有两个刻度都是“2”，但-2℃是0下面的这个刻度“2”，这是因为-2℃表示的是零下2℃，就是比0℃还要低2℃，自然是0下面的刻度“2”。因此，以0℃为分界点，从0℃起往上，越往上温度越高；从0℃起往下，越往下温度越低。由此可见，正数、负数均有方向，且方向相反。

想法2（关于走路）：如图2所示，从这棵树出发，往东走1米，可以用“＋1米”表示。同样，往西走1米，可以用“－1米”表示。那么，这棵树就是正、负数的分界点，可用0来表示。

教师提出问题：“是否向东走用正数表示，而向西走用负数表示呢？”

从图2所示的“＋5”这一点出发，往西走2米，到达“＋3”这一点，该点是否可以用“－2米”来表示呢？学生开动脑筋、各持己见，在深入探究后生成结论。

问题6：结合上述想法，如图3所示，可以用数轴表示正数与负数。观察数轴，你们发现了什么？

学生在深度思考与交流后明晰：“0是正、负数的分界点，它既不是正数也不是负数” “正、负数都有方向”“以0为中心，每个正数均有一个与之对应的负数”。

设计意图：教师以实例为素材，拾级而上地引导学生进行深度思考、探究与交流，让学生在师生交流和生生互动中切实理解负数的意义，实现数系的自然拓展，对概念本质的理解与建构水到渠成。

3. 教学环节3：切实应用，拓展思维

问题7：列举人们在日常生活中用正、负数表示信息的例子。

问题8：综合上述例子，你能归纳正、负数的共同特征吗？

设计意图：教师利用实例的扩展引起学生的认知冲突，引导学生进一步厘清正数、负数和0之间的关系，切实体会负数的实际应用价值，增强认数的活动经验。在整理中，教师给予学生充分的时机探索与表达，以提升学生的数学思维品质，培养学生的高阶思维能力。

4. 教学环节4：反思提炼，深化思维

问题9：回顾本节课的学习过程，我们是如何认识“负数”这个新朋友的？

问题10：你还想知道哪些关于负数的知识呢？

设计意图：及时反思、梳理和提炼是课堂教学的深化，可以让学生经历知识的再认识和再创造过程，以深化理解和认识，培养有效的数学学习能力。

二、培养学生数学高阶思维能力的思考

1. 聚焦学情，真实体验是培养高阶思维的前提

教师要通过有效的活动来培养和发展学生的数学思维，提高学生的数学核心素养。教师从学生的生活实际、已有知识水平着手创设多样化的问题情境，设计挑战性的学习任务，可以激发学生的好奇心、求知欲和探究欲，促进学生的深度学习。本课中，教师在课前让学生搜集关于负数的实例，为学生在课堂中有意义经验的生成做足准备。更重要的是，整个教学中教师从学生的实例出发创设问题情境，设计实践性和探究性的活动，能撬动学生的思维，引导学生经历深度探究的过程，最终在真实体验中形成自己的认知经验，促使其高阶思维能力的逐级跃升。

2. 巧妙设问，引发探究是培养高阶思维的源泉

在具体教学的过程中，教师要创设问题情境。学生高阶思维的形成与发展无法通过知识的直接传输获得，需要学生在操作、猜想、实践、思考和创造中逐步形成与发展。当然，学生思维的形成离不开问题的支撑，问题不是随意预设的，需要指向学生深度思考和探究。实践证明，有效的问题有利于发展学生的思维。本课中，教师提出问题引导学生思考，促使学生拾级而上地探究，让学生自然构建知识框架。

3. 学会等待，充分“让学”是培养高阶思维的关键

在数学教学中，教师要给学生留足尝试和探究的时间和空间，促进学生思维的发展。问题解决后教师留足时间让学生及时反思，可以实现探究经验的内化，从而水到渠成地发展学生的数学核心素养。教师要充分地让学引思，创新学生的数学思维方式，真正意义上发展学生的高阶思维。本课中，教师在教学过程中时刻关注生成的教学资源，并留足时空让学生探索、合作和反思，促使学生在深度学习中水到渠成地发展高阶思维能力。

总之，教师要从“以生为本”的理念出发，紧扣知识内核，创设问题情境，充分地让学，引导学生亲历具有思维含量的数学探究活动，在深度探究、深度合作中培养其联想、质疑、反思、迁移等高阶思维能力。