思维生长：让数学学习朝向深度建构

［摘  要］ 学生的天性好奇又具有探索性，教师不能“禁锢”学生的思维，要创设条件给学生一个深度思探的机会。教师应将适合学生思探的知识点设计成教学情境让学生审问、慎思、广议、明辨，通过经历数学、感悟数学、运用数学，使学生在数学知识思探中获得数学知识，让数学学习朝向深度建构。

［关键词］ 行知思想；思维生长；数学学习；深度建构

陶行知先生说：“千教万教教人求真。”在数学教学过程中，教师要教会学生“爱思维、真思维、活思维、善思维”，朝向积极的深度思维“挺进”。

从2019年起，笔者一直在开展“让数学学习朝向深度建构”专题实践与探索，历经课堂调查、分析研究、实践论证、理论提升、实践再论证等过程，进行反复循环实践验证，取得了较为丰富的实践经验，并与多所学校进行了多次相关研讨活动，产生了一定的辐射效应。

一、理性解读：数学深度思维建构的双维思考

1. 学生“深度思探学习”现状剖析

笔者针对近3年观摩的320余节数学课进行系统分析，发现课上学生“思而不乐”“思而不深”“思而不清”等现象约占47%。

《义务教育数学课程标准（2022年版）》（以下简称新课标）指出，学生要“会用数学的眼光观察现实世界”“会用数学的思维思考现实世界”。然而，部分教师在课前设计了很多琐碎的小问题，希望能够激起学生思考的兴趣，让其通过探索、合作，从而自主获得新知。因为教师没有基于学生思维生长特点，围绕教学目标设计教学预案，在有效思维、深度思维上考虑不够深入，因此问题呈现“表层化”“繁杂化”“零散化”等问题。这些问题虽然能够让学生很容易获得答案，但是从发展学生思维的角度来看没有太大的价值。

案例1  两位教师执教一年级下册“认识人民币”

A教师

师：动物王国的狮子大王要给小猪、小鸡、小狗、小兔发红包，你们爸爸妈妈给你们发过红包吗？

师：狮子大王的这个红包漂亮吗？想知道狮子大王为什么要给小猪发红包吗？红包里面装着什么呢？猜猜看。

生1：我猜是人民币。

师：你真聪明，我们一起来看看吧。（出示人民币1元）这是什么？

师：我们一起说1元。你们知道1元钱能买到什么东西吗？

此案例可以看出，A教师在创设情境时花了一些心思，学生一定学得“很欢”，但在“欢天喜地”之下，却是无效化问题。“苍白”的问题无法激起学生深度的思考，只剩童趣而已，缺乏数学课应有的思维味。

B教师

师：动物王国狮子大王要给小猪发红包，聪明的小朋友替狮子大王想想，红包里放什么比较合适？

生（异口同声）：放钱。

师：是啊，过年时爸爸、妈妈、爷爷、奶奶一般都是在红包里放压岁钱，这是中国人过年的习俗，是对我们的美好祝福。你们见过怎样的钱呢？

学生纷纷说有人民币、美元、欧元等。

师：是啊，地球是一个美丽的大家园，钱包里的钱是丰富多彩的。但祝福是一样的，都是大人对我们的爱。那狮子大王在红包里放了哪国的钱呢？让我们一起来猜一猜、认一认。

师：是啊，这些钱都是我们国家的人民币。谁来说一说你是怎样猜的？

从上述案例可知，教师在课堂上不仅是知识的传授者，还应该是学生思维的引路者。教师不仅要联系学生的生活经验，激发学生思考的欲望，还要为学生的思维向纵深挺进“铺路架桥”，从而提升学生思维的敏锐性、深刻性。而B教师既能够捕捉知识的思维生长点，又能融合民俗进行爱国主义教育。教师的问题设计要具有教学艺术性，能让学生在“摸—思—说”中进行深度的思考。在教学中，B教师颇具教学智慧，他的问题“点到为止”，不纠缠，可谓恰到好处。

2. 学生“深度思探学习”的价值取向

（1）找准思维基点——尊重学生的思维差异，让学生思维“拾级而上”

小学生的思维方式带着一份儿童味，常常用“自以为是”的方法来解答。教师要用“特别的眼睛”观察和关注学生，并尊重他们的思维方式和思维结果。有的学生数感很强，有的学生需要借助几何直观才能解答，有的学生只会“计算”。教师要尊重学生的差异，让每个学生都获得相应的思维训练和提升。比如，问题“0.33333×0.33333”，如图1，教师在学生积极自主探究的基础上设计了三种方法，帮助学生理解和求出答案。教师针对学生思维力差异创设了不同的思维空间，给学生找到相应的导思方法，巧妙地把0.33333×0.33333转化为逐层思探的过程，化难为简，收到很好的效果。无论是“找规律法”“列竖式计算法”“线算法”，还是直接用“计算器计算法”，都不能淡化思维训练，教师要引导学生经历从“表象→规律→结果”，或“结果→规律”的过程。不同学情、不同思路、不同方法，但殊途同归，像这样有梯度的思维碰撞能让数学课堂更有数学“发现”的味道。

（2）延展思维生长点——发展学生的思维意识，让学生“扶摇直上”

给学生一个深度思探的平台可以延展思维生长点，教师要相信学生思探的能力，让学生乐于探究。

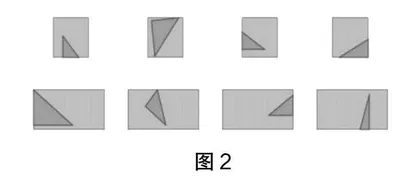
在一节数学活动课上，教师出了一道开放题：“在1张正方形或长方形纸片上剪去1个三角形，剪去的三角形至少有1条边或1个顶点在正方形、长方形的1条边上。有多少种不同剪法？”

学生纷纷开始操作起来，在操作结束后进行交流。如图2，教师要求学生把自己剪的结果在黑板上展示出来（必须是不同的），并启发学生思考：你们从这组图中发现了什么规律？在短短的5分钟时间里，学生们纷纷把自己的观察发现与伙伴分享。

开放的形式，活跃的思维，多种的答案，在探索与相互欣赏中每个学生的思维得到了最大限度的发展。精彩的“观察、找规律、交流”点亮了数学课堂，使学生不仅学到了更多解决问题的策略，掌握了数学技能，还认识到了交流和倾听的重要性。

（3）触摸思维最高点——升华学生的数学素养，让学生思维“青云直上”

思维的最高点就是学生运用所学知识进行自主探索创新。在数学教学中，为了让学生巩固所学的新知，教师要提供问题情境，通过改变习题的内容和练习的方式达到巩固训练的目的。在练习过程中，教师要充分挖掘教材，积极引导学生，使学生产生更多的联想与创新，使每个练习发挥最大的功效。

在教学“年、月、日”的知识时，教师设计了一道题：2001年的元旦是星期一，那么2002年元旦是星期几？一个学生利用学过的方法，用2001年全年的365天除以7就算出有52个星期还余1天，把2001年的元旦星期一加上余下的1天得到2002年的元旦是星期二。教师及时肯定了这名学生的方法迁移很有价值。然后，教师设计了新问题：2021年10月1日国庆节是星期五，那么2022年10月1日是星期几？学生用多种方法进行解答，有的直接回答，有的通过计算，有的相互协作完成。

自疑、自探、发现是思维重要的因子。学生带着“方法迁移”的思维习惯，会不断迸发出思维创新的火花。教师及时的理答和引导能促使每一位学生成为课堂上的积极参与者和合作者，从而使每个学生都成为思辨者、释疑者、创新者。

二、思探课型导学：让数学学习走向深度建构

新课标指出：“能够合乎逻辑地解释或论证数学的基本方法与结论，分析、解决简单的数学问题和实际问题。”思探教学课型是给学生一个解释、论证以及分析、解决问题的“窝”，给学生学习铺设一条深度思维的路径，让学生的思维在问题探索中有深度、有发散、有创新，在思维拔节的时空中，使数学学习走向深度建构。

思探教学概括起来就是：先探后教，学生先围绕学案进行有目标的自探；然后教师根据学生自探情况进行点拨、查漏补缺、提供训练题目，提升学生思维能力。

1. “传统教法”与“思探教学”教法比较

详情见表1。

2. 思探课型教例——以“小数加法和减法”的教学设计为例

环节一：激疑先探、激活思维

（1）观察思考，如图3，启思：你发现了什么？出现这样情况的原因是什么？

（2）思探例题

师：我们已经学会了整数的加减法，这一节课我们要继续学习小数的加减法。如图4，请同学们思考，时间为5分钟。根据题中信息，求“小明和小丽一共用了多少钱”就是求（    ）与（    ）之（    ）。

估一估：结果可能为（    ）元。

算一算：列竖式计算。

想一想：用列竖式计算小数加法时，把两个加数的（    ）数位对齐，然后从（    ）位算起，把相同数位上的数相加，满（    ）进（    ）。

验一验：我是这样验证刚才计算的结果对不对的。

（3）交流思探

师：通过刚才的思探，哪位同学来分享一下自己的成果呢？（学生汇报）

师（查漏补缺）：列竖式时，先回忆一下整数加法时把什么对齐？

生（齐声答）：个位对齐，也就是相同数位对齐。

师：那么小数加法呢？

教学预设：如果学生说出是相同数位对齐，教师出示4.75，让学生分别说出每一个数位，再追问几和几对齐。

教师边板演算式边提问：对齐后，从哪一位开始算起？

生1：和整数加法一样，也是从低位算起。

师：你们做得正确吗？如何验证自己的计算结果？

师（课堂小结）：刚才，我们用竖式计算了小数的加法，谁来完整地说一说在计算小数加法时应该怎么做？

生2：把两个加数的相同数位对齐，然后从低位开始算起，把相同数位上的数相加。（指名说，齐说）

师：同学们真棒，这么快就探索出小数加法的计算方法，想不想继续接受挑战？

生（齐声答）：想。

师：好的，请同学们继续看学案2，时间为3分钟。

环节二：例题深探、逐步建构

（1）思探题

①求小明比小丽多用多少元？可以怎样列式？

②如图5，小明列的竖式正确吗？为什么？那你是怎样列竖式的？你想给小伙伴提醒什么？

（2）探学交流。

师：同学们，谁来展示一下自己的列式？

师（追问）：让什么对齐？

生（齐声答）：相同数位对齐，也就是小数点对齐。

教师出示算式，边板演边问：从哪一位开始计算？

生（齐声答）：低位。

师：5的下面没有数怎么办？

生3：相当于减了0。

师（小结）：同学们，你们认为在计算小数的减法时有什么要注意的地方吗？

生（齐声答）：要让相同数位对齐，就是小数点对齐，还有空位是“0”。

环节三：应学导练、夯基提能

师：刚才同学们计算了小明和小丽一共用了多少元，小明比小丽多用了多少元，现在小芳也想让你帮她解决几个问题，有信心吗？

生（齐声答）：有。

师（出示试一试）：大家分组完成，每一大组完成一小题，结果要按照老师的要求做哦！

学生汇报，板演四个竖式。

师：你们能把计算结果化简吗？是根据什么来化简的？

师（小结）：大家想想，小数加减法与整数加减法有什么相同点？在计算小数加减法时有没有要提醒同学们注意的地方呢？

环节四：梳理总结、完善建构

通过今天的学习，你们有哪些收获？有什么疑惑吗？下面我们走入“小老师夏令营”，看看大家有哪些收获？（多种形式的练习）