在实践探索中走向深度学习

［摘  要］ 在小学数学教学中，教师应贯彻“以生为本”的教学理念，结合教学实际设计实践活动，让学生的思维在实践探索中走向深入。研究者以“正比例图像”教学为例，让学生通过描点、连线等活动，初步认识正比例图像；借助几何直观，培养学生数形结合意识，提高学生深度思维的能力。

［关键词］ 以生为本；实践活动；深度思维

在“正比例图像”教学中，教师以学生的已有认知为起点，结合教学实际精心创设问题，让学生在问题的引导下初步认识正比例图像的特点及要素。同时，教师引导学生在变化中抽象不变的规律，以加深学生对正比关系中变化规律的认识，提高学生自主探究能力，提升教学的有效性。

一、教学过程

1. 回顾旧知，复习引入

师：上节课我们学习了有关正比例的知识，谁来说一说当两个量存在怎样的关系时，它们成正比例呢？

生1：当两个量的比值总是一定时，这两个量就是正比例关系。

师：如果用一个关系式来表达，可以如何表达呢？

生2：=k，其中x和y表示相关联的两个量，k表示它们的比值。

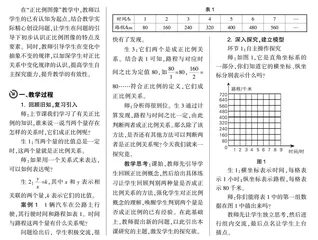
案例1  1辆汽车在公路上行驶，其行驶时间和路程如表1。时间与路程这两个量有什么关系呢？

问题给出后，学生积极交流，很快有了发现。

生3：它们两个是成正比例关系。结合表1可知，路程与对应时间之比为定值80，如=80，=80……符合正比例的定义，它们成正比例关系。

师：分析得很到位。生3通过计算发现，路程与时间之比一定，由此判断两者成正比例关系。那么除了该方法，是否还有其他方法可以判断两者是正比例关系呢？今天我们就来一探究竟。

教学思考：课始，教师先引导学生回顾正比例概念，然后给出具体练习让学生回顾判别两种量是否成正比例关系的方法，强化学生对正比例概念的理解，唤醒学生判别两个量是否成正比例的已有经验。在此基础上，教师提出新的问题，以此引出本课研究的主题，激发学生的探究欲。

2. 深入探究，建立模型

环节1：自主操作探究

师：如图1，它是直角坐标系的一部分，你们知道它的横坐标、纵坐标分别表示什么吗？

生1：横坐标表示时间，每格表示1小时；纵坐标表示路程，每格表示80千米。

师：你们能将表1中的第一组数据在图1中描出来吗？

教师先让学生独立思考，然后进行组内交流，最后点名让学生上台描点。

师：大家看看他描点的位置对吗？（生点头表示赞成）

师：谁来说一说，你是如何确定点的位置的？

生2：我是先在横轴上找表示1小时的点，然后在纵轴上找表示80千米的点，最后分别作平行于y轴和x轴的直线，两直线的交点就是所求的点，其表示1小时行驶80千米。

师：非常好，按照这种方法，你们能找出其他各组数据对应的点吗？

生（齐声答）：可以。

教师预留时间让学生描点。

师：连接图中各点，看看你有什么发现？

生3：这些点正好在一条直线上，而且是从左下向右上延伸。

师：这条线的起点在哪里呢？

生4：表1中的第一组数据就是起点。

生5：我不同意，汽车怎么可能一下子行驶80千米呢？我觉得应该将0小时0千米作为起点。

师：非常好，考虑得非常全面。起点就是这个点（教师在图1中指出该点），就是生5所说的0小时0千米。这个点在直角坐标系中叫作“原点”。

师：现在我们让汽车动起来。

教师动画演示汽车在0～1之间行驶，让学生观察图像的变化。

师：这条线段表示什么意思呢？

生6：表示汽车从起点出发，行驶1小时的距离。

师：这段距离呢？汽车行驶了几小时，距离是多少呢？

教师继续动画演示汽车在1～2小时之间行驶。

生7：汽车行驶了1小时，其行驶距离为80千米。

师：很好，还可以怎样表示呢？

生8：汽车从起点出发，行驶了2个小时，共行驶了160千米。

接下来，教师继续进行动画演示。最后，教师演示小汽车开出画面，图像也随之延伸出画面。

师：汽车能像这样一直开下去吗？

生9：我认为可以，如果不设定终点，汽车可以一直行驶下去。

生10：这应该是一个理想状态，但是要保证汽车有用不完的油。

师：说得很有道理。我们设想汽车有足够的油，在不设定终点的情况下可以一直开下去，这条直线向右上一直延伸下去。这条无限延伸的直线就是我们今天学习的正比例图像。

教学思考：出示直角坐标系（第一象限），让学生在这个直角坐标系中描点、连线，初步完成图像的建构。这样借助图像直观帮助学生充分感受随着时间的变化，其行驶路程也随之变化的规律。在此过程中，教师让学生思考“起点在哪里”，启发学生结合生活实际解决问题，培养思维的缜密性。此外，教师动画展示小汽车的行驶过程，让学生体会用图像刻画数量间的变化规律，培养学生数形结合意识。

环节2：合作交流，探寻图像特点

师：观察图像，你们还有哪些发现？

生1：直线上的点所表示的是路程和时间这两个相关联的量。

生2：当时间发生变化时，路程也随之变化。

生3：汽车行驶的时间增加，其行驶的路程也增加。

师：大家通过观察不仅发现一个量随着另一个量的变化而变化的规律，而且发现两个量是同时增加的规律，非常棒！那从变化的规律中，你们是否看到了不变的本质呢？

生4：尽管路程随着时间的变化而变化，但是两者的比值不变，也就是速度不变。

生5：我还发现，不管时间和路程如何变化，只要其中一个量确定了，那么另一个量也就确定了。比如，汽车行驶2小时，它的行驶距离就是160千米；若汽车行驶240千米，那么它的行驶时间为3小时。

师：很好，也就是说，已知时间，则有唯一的路程与之对应；已知路程，则有唯一的时间与之对应。你能进一步解释一下吗？

生5：因为路程和时间的比是不变的，就是说汽车行驶的速度不变，所以若时间（或路程）确定了，那么相应的路程（或时间）也就确定了。

师：非常好，其实很多变化都是有规律的，我们要学会用数学的眼光看世界。

师：通过以上操作、观察、分析等活动，我们掌握了正比例图像的一些特点。不计算，你们能根据给出的路程或时间来判断其对应值吗？

生（齐声答）：能。

师：汽车4小时行驶了多少千米？汽车行驶400千米需要多少小时？

问题给出后，学生在图中操作，很快有了答案。

生6：首先在横轴上找到4小时，它刚好在格点上，沿着方格线向上看，找到方格线和图像的交点；然后顺着交点向左看，它在纵坐标上所对应的值为320，就是说汽车4小时行驶了320千米。

师：很好，你能在图像上找到行驶400千米所需的时间吗？

生7：其实和刚才的方法是一样的，不过这次需要从纵轴出发，在纵轴上找到400千米，沿着网格线向右看，找到网格线和图像的交点；然后从交点沿着方格线往下看，它与横轴的交点是5，就是说汽车行驶400千米需要5小时。

师：刚才我们找的点有什么共同的特征吗？

生8：这些点刚好在方格线上。

师：如果这些点不在方格线上，是否能够在图像上找到对应的值呢？比如，汽车2.5小时行驶了多少千米？

生9：可以，其操作方法是一样的，可以在横轴上找到2.5这个点，从这点出发，作平行于纵轴的直线，找到直线与图像的交点；然后从交点出发，作平行于横轴的直线，这条直线与纵轴的交点就是我们要找的对应值。

师：很好，请大家动手做一做，然后给出你的值。（学生积极操作）

生10：这个点不在格点上，所以不一定得到准确值，我估计了一下，这个点对应的数值大约是200千米。

师：这里的“估计”和“大约”用得非常恰当。我们一起来看一下刚才的操作过程。（教师动画演示，得到图2）

师：如果汽车行驶360千米，需要多长时间呢？

教师让学生自己操作，然后与同学进行交流。

生11：先在纵轴上找到表示360千米的点，从该点出发向右作平行于横轴的直线，找到直线与图像的交点；然后从交点向下作平行于纵轴的直线，该直线与横轴的交点即为我们要找的点。根据图像我估计了一下，应该是4.5小时。

师：这样利用图像，我们可以根据一个量找到对应的另一个量。借助图像，你们还有什么发现？

生12：还能看出汽车1.5小时可以行驶120千米。

生13：汽车行驶720千米需要9小时。

……

师：在正比例图像上有无数个点，你们知道这些点有什么共同点吗？

生14：它们都表示速度为80千米/时。

师：在变化中寻找不变的关系，让数学变得更有魅力。

教学思考：教师引导学生充分挖掘图像中隐含的信息，让学生在“变”与“不变”的比较中厘清正比例图像的特点和要素，提升学生自主探究能力。此外，教师引导学生应用图像估值，让学生将“数”与“形”有机结合在一起，在求同比较中发展学生推理能力，提高学生数学素养。

3. 巩固练习，完善认知

案例2  小红打字时间和打字数量如表2。根据表2数据，你能判断打字数量和打字时间成正比例吗？给出你的理由。

案例2 与案例1研究的内容基本一致，属于基础练习，教师让学生独立完成。从学生反馈来看，有的学生从“数”的角度出发，通过计算发现“打字数量与打字时间之比为定值”，根据正比例概念判别两个量成正比例；有的学生从“形”的角度出发，通过描点、连线，根据图像判断两个量成比例。

案例3  小军和小明周末骑车去游乐场玩，他们两次骑行的路程和时间的关系如图3和图4，你能根据图像判断这两次骑行的路程和时间成正比例吗？说一说你的理由。

该题主要考查学生对正比例图像特点的掌握情况。解题前，教师引导学生根据以上练习对正比例图像的特点进行归纳总结，学生发现：正比例图像是一条经过原点的，从左下向右上延伸的直线。

师：根据图像你们是否能判断骑行时间和路程成正比例关系？

生1：图3不是，图4是，因为图3中的图像不是一条直线，而图4中的图像是一条直线。

师：非常好，你根据正比例图像的特点给出了判断。如果让你们验证这个判断是否正确，你们该如何验证呢？

生2：可以看看路程和时间的比是否一定，如果该比值一定，那么它们就是正比例关系，否则不是。

师：很好，请大家验证一下。

生3：图3中，=，=，显然其比值不是一定的，所以它们不是正比例关系。图4中，路程与时间之比均为，所以它们成正比例关系。

师：很好，对于以上两种判别方法，你们更喜欢哪个呢？

生4：我喜欢用图像来判别，图像更加直观，一目了然。

师：很好，现在我们在原有情境的基础上变一变，你们有什么发现？（教师给出案例4）

案例4  小军和小明两人周末相约去游乐园玩，图5是他们骑行路程和时间的关系。图5与刚才的图像相比有何不同，你们有什么发现？

教师先预留时间让学生互动交流，然后展示学生交流成果。

生1：图4中有一条直线，表明小军和小明的速度是相同的。图5中是两条直线，表明他们骑行的速度不同。

师：如果骑行的距离是16千米，根据图像你们能判断谁先到达吗？

生2：小明先到达，结合图像可知，小明骑行16千米需要40分钟，小军骑行16千米需要60分钟。

师：很好，仅根据图像，你们能判断他们两人谁的速度更快一些吗？

生3：小明的速度更快一些，因为除了原点外，虚线一直在实线的上方。

生4：图像与横轴所成的角度越大，速度越快，所以小明的速度更快一些。

师：说得非常有道理，大家不仅善于观察，而且善于推理，这样利用图像可以快速解决问题。

教学思考：在练习阶段，教师以现实生活为依托，引导学生应用所学知识解决实际问题，这样既提升了学生的解题技能，又让学生感悟了“学以致用”的真谛。同时，在此过程中，教师鼓励学生进行总结归纳，进一步强化对正比例图像的特点和要素的理解，让学生充分感知图像的直观、形象、简便等特点，促进学生直观想象素养的培养和数学能力的提升。

4. 课堂小结，内化知识

该环节教师引导学生回头看，对所学知识、方法、思想等进行总结归纳，组织学生进行互动交流，帮助学生积累活动经验和提高学习能力。

教学思考：课堂小结是课堂教学的重要组成部分，是学生将知识内化为能力的重要途径。教学中，教师要预留时间让学生进行反思回顾，以逐渐完善学生的认知体系，提高学生的认识水平。

二、结语

在小学数学教学中，若想引发深度思考，让学生学会学习，教师要少一些讲授，多提供一些机会让学生自主探究，引导学生在“变与不变”中探寻数学规律，以提高学生学习的主动性、积极性。在“正比例图像”教学中，教师从学生已有的正比例概念入手，让学生在比较中找到判断正比例关系的另一种方法，进而让学生感知图像在解决实际问题中的直观性，培养学生数形结合意识，提升学生数学素养。

总之，在小学数学教学中，教师应结合教学内容和学生学情创设一些有价值的问题，让学生在解决问题的过程中学会思考、学会探索、学会归纳，提高其深度思维的能力。