数学实验：优化学生思维品质的新门径

［摘  要］ 数学实验是优化学生数学思维品质的门径：实验猜想能让学生的数学思维有广度，实验操作能让学生的数学思维有新度，实验想象能让学生的数学思维有深度，实验反思能让学生的数学思维有温度。教师要精心设计、研发、实施数学实验，让数学实验成为驱动学生主动思维、提升学生思维品质的重要载体、媒介，让数学实验为学生的数学学习“铺路架桥”。

［关键词］ 小学数学；数学实验；思维品质；优化门径

数学实验是学生数学学习的一种重要路径。数学式观察、数学式调查、数学式操作等都是学生数学实验的有效方式。数学实验不仅能引导学生建构知识，而且能优化学生的思维品质，让学生感悟数学思想方法。教师要充分发挥数学实验对学生数学思维品质提升的功能，彰显数学实验对学生数学思维品质优化的价值。数学实验是促进学生数学思维品质生成、发展、提升的新门径。在数学实验过程中，学生能积极主动地投入数学学习中来，能进行有深度、有质量的数学思维、探究。

一、实验猜想：让学生的数学思维有广度

思维的广度是学生思维品质的重要方面，思维广度表征与确证的是学生思维的指向性。在数学教学中，笔者发现有时候学生的思维面、思维路径比较窄。借助数学实验的猜想能有效激发学生的思维兴趣，调动学生的思维积极性，让学生敢于、勇于、善于、乐于进行数学思考，从而让学生的数学思维具有宽广性。实践证明，经常让学生进行数学实验猜想，学生的思维活跃度就会比较高；如果教师淡化学生的猜想，甚至压抑学生的猜想，学生的思维就会越来越狭窄，最终陷入思维僵化、思维凝固等境地。

在数学教学中，教师要为学生营造良好的数学实验猜想的情境，给学生打开实验猜想的平台，赋予学生数学实验猜想的时空、权利等。只有这样，学生才能积极、主动地猜想［１］。甚至，学生能突破自我的认知习惯、思维定式等，从而进行发散性、多维度、多层次的猜想。对于学生的猜想，教师要多鼓励、多点拨，从而建构一种“踊跃猜想”的学生数学学习格局［２］。教学“平行四边形的面积”这一部分内容时，笔者引导学生猜想：平行四边形的面积与什么有关？如此，学生纷纷根据实验操作提出自己的猜想。

猜想1：认为“平行四边形的面积与平行四边形的底和斜边的长度有关”，因为用长的小棒做成底和斜边比用短的小棒做成底和斜边所得的平行四边形更大些；

猜想2：认为“平行四边形的面积与底和斜边的长度有关”，根据平行四边形可以推拉成长方形，而长方形的长、宽分别相当于平行四边形的底和斜边；

猜想3：认为“平行四边形的面积与平行四边形的底、斜边和夹角的大小有关”，因为平行四边形在推拉成长方形的过程中，平行四边形的四个角的大小都发生了变化；

猜想4：认为“平行四边形的面积与底和高的长度有关”，因为平行四边形可以剪拼成长方形，长方形的长和宽分别相当于平行四边形的底和高。

显然，这里学生的猜想都是有理有据的猜想。这些根据是学生在对平行四边形的相关简单操作、实验基础上生发的，都确证与表征了学生对影响平行四边形的面积大小相关因素的认知。教学中，教师必须注重学生的猜想，利用学生的猜想，让学生的猜想发挥教学功能。

猜想是实验发现的前奏，也是实验开展的基础［３］。通过猜想，学生能提出相关的问题；通过猜想，学生能进行积极的数学尝试、数学思考、数学探究。猜想让学生的数学实验活动成为一种理智历险、理智探险的活动。

二、实验操作：让学生的数学思维有新度

实验操作是数学实验的核心环节。实验操作要让学生真正地“做数学”，让学生通过“做”的方式将相关数学知识建构、创造出来。因此，学生的数学实验操作往往蕴含着学生的思维，是在学生的数学思维导引、驱动下开展的一种自然、自觉、自发的活动。在数学实验操作过程中，教师要给学生提供相关的结构性素材、结构性资源，充分发挥学生实验操作的主观能动性，让学生的实验操作成为学生本质力量的确证与表征，成为学生的生命实践活动。

比如教学“三角形的三边关系”这一部分内容时，笔者综合各方面的因素，设计了一组实验素材，将实验操作切入学生数学学习的“最近发展区”，让学生的数学实验操作富有挑战性。

材料：1根10cm的蓝色小棒，6cm、10cm、12cm的黄色小棒若干根。

实验1：从6cm、10cm的黄色小棒中选择1根，将其任意剪成两段，能与蓝色小棒围成三角形吗？

实验猜想1：能围成三角形或不能围成三角形。

学生开展实验操作。

实验思考：为什么能或不能围成三角形？

实验2：用1根12cm的黄色小棒，将其任意剪成两段，能与蓝色小棒围成三角形吗？

实验猜想2：能围成三角形或不能围成三角形。

学生开展实验操作。

实验思考：为什么能或不能围成三角形？

这样的实验设计不仅选择了结构性的实验素材、实验资源，而且选择了结构性的实验操作组织方式，让学生的数学实验过程有层次、有阶梯。其中，“实验1”让学生认识了不是任意的3根小棒都能围成三角形，如果2根小棒的长度和比第3根小棒的长度还要小，那么这样的3根小棒不能围成三角形。“实验2”以“12cm”的小棒作为素材，进一步探究“三角形的三边关系”，从而让学生建构起“任意两条边的和都必须大于第三条边”的数学实验结论。

实验操作是学生的一种手脑协同活动。教师要优化学生的实验路径，为学生的数学实验创设条件，借助数学实验催生学生的数学思维，让学生自主建构、创造知识，让学生从数学学习的“看客”转向数学学习的“创客”，让学生的数学实验不断升级。

三、实验想象：让学生的数学思维有深度

想象是数学实验的必要补充，是丰富数学实验内容、形式的重要策略。通过数学实验的想象能让学生逼近数学知识的本质，让学生的数学实验有思维的深度。学生的数学学习就是学生数学操作与数学想象的“珠联璧合”。教师要善于引导学生的想象、催生学生的想象，让学生想得合理、想得科学。

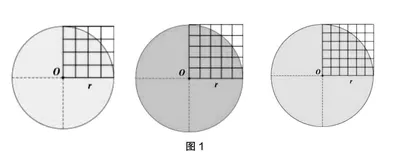
为了优化学生的想象，教师在教学中要引导学生直面数学问题本身，要从数学问题本身出发，把控学生的思维方向。通过想象，学生还能克服数学实验的某些不足，或者数学实验无能为力的地方，或者数学实验不到位的地方等。实验想象让学生的数学实验收获更丰富、完善。比如教学“圆的面积”这一部分内容时，笔者应用多媒体课件呈现方格图，将圆放置到方格图中，引导学生用数方格的方法，统计圆的面积大约是正方形面积的多少倍，由此猜想圆的面积和小方格的关系，也就是猜想圆的面积与半径的平方之间的关系（如图1）。

在学生猜想的基础上，笔者引导学生开展数学实验。学生分小组开展实验：“小组1”将圆平均分成8份，然后拼成近似的长方形；“小组2”将圆平均分成16份，然后拼成近似的长方形；“小组3”将圆平均分成32份，然后拼成近似的长方形。

在此基础上，笔者借助多媒体课件动态呈现圆被平均分成若干等份，拼成近似的长方形的过程。在多媒体的演示中，学生直观地看到，圆被平均分的份数越多，所拼成的近似的长方形也就越接近长方形。由此，学生进行动态的想象：将圆平均分成64份、128份、256份等后会如何？在动态的想象中，学生的头脑中构建了一个圆演变为长方形的动态发展过程。这一过程建立在学生数学实验的基础之上，但超越了数学实验。教师要有意识地引导学生将数学实验与合情想象、合理想象等结合起来，从而深化学生的数学体验，深化学生的数学认知。通过实验想象，不仅能促进学生对实验结果的认同，而且能促成学生对实验过程的认知，这其中融入了数学思想，如极限思想、转化思想、对应思想、建模思想等。

在引导学生数学实验想象的过程中，教师要把控学生的想象走向，要助推学生寻求正确的想象路径，同时相机融入相关的想象方法。通过数学实验想象，学生对数学实验内容、实验结果、实验过程等不仅“知其然”，更“知其所以然”。实验操作与实验思维、实验想象等是数学实验的两翼，它们相辅相成、相得益彰、相互促进、共生共长。

四、实验反思：让学生的数学思维有温度

实验反思是实验的一个必要的环节。如果学生在数学实验中不注重反思，那么学生极容易沦为一个简单的操作工。因此，教师在学生的数学实验中要注重引导学生反思，培养、提升学生的实验思维品质。教学中，教师不仅要引导学生在实验后反思，而且要在实验过程中进行反思，甚至在实验前进行“前反思”。反思，让学生的数学实验更加理性、理智，让学生的数学实验更有序、更富层次性，让学生的数学实验更有效度、信度。

实验反思让学生的数学实验突破碎片化、单子式的模式，走向一种实验整体、实验结构。实验反思让学生的数学实验更具系统性。比如在教学“圆的周长”这一部分内容时，笔者发现学生在数学实验中出现了很多可以避免的错误。为了激发学生的实验思维，笔者引导学生在应用“滚圆法”“绕圆法”测量圆的周长的基础上进行反思：为什么自己几次实验的结果不同？为什么不同小组测量相等直径的圆的周长，测量结果却不同？在反思之中，学生进一步检视自己的实验工具、实验过程、实验方法等，从而催生了学生的实验思维。这样的实验思维让学生的数学学习更有温度。

反思1（生1）：我之所以每一次测量圆的周长的结果不同，是因为我在滚圆的过程中，没有做记号，让圆多滚了一点距离或少滚了一点距离。

反思2（生2）：我在实验过程中没有将棉线紧贴圆周上，导致实验结果不准。

反思3（生3）：我用的是滚圆法测量圆的周长。我滚圆的时候不是沿着直线滚的，导致实验结果不准。

反思4（生4）：我用的是绕线的方法来测量圆的周长的，在绕线的过程中线比较松弛，导致测量结果不准。

通过实验反思，学生改进了实验，让实验操作不断走向规范、科学。学生用实际测量结果计算的时候，算出来的值虽然有差异，但是非常接近（有学生计算圆的周长和直径的比值精确到4位小数），由此进一步引发了学生的深度思维。

反思1（生5）：老师，我认为圆的周长除以圆的直径可能是除不尽的。

反思2（生6）：老师，我认为圆的周长和圆的直径的商可能是小数，并且小数的位数非常多。

在学生深度反思的基础上，笔者呈现了圆周率的发展史，让学生了解古人对圆周率的探索。比如刘徽的“割圆术”、祖冲之的“约率”与“密率”、现代计算机计算的圆周率的位数。有了学生的实验反思，学生对圆周率是一个“无限不循环小数”（即无理数）有了深刻的体验。这样的体验能深化学生对圆周率的认知，让学生触摸无限不循环小数的“无限”“不循环”的特性。

数学实验是学生重要的数学学习方式，真正的数学实验一定蕴含着学生的数学思维，并且一定能让学生的数学思维走向睿智与深刻。教师在数学教学中要精心设计数学实验方案，有效组织、实施数学实验，让学生充分经历数学实验的过程，引导学生自主实验、自能实验，不断提升学生的数学实验能力。只有这样，学生才能真正借助数学实验建构数学知识、积累活动经验，让数学实验为自己的数学学习“铺路架桥”。

参考文献：

［１］ 郑毓信.数学教学与学会思维——“教数学、想数学、学数学”系列之四［Ｊ］. 小学数学教师，２０１５（６）：４－１１.

［２］ 潘小福，陈美华. 小学数学实验教学理论与实践［Ｍ］. 南京：江苏凤凰教育出版社，２０１８.

［３］ 潘小福.小学数学教材的专业化解读［Ｍ］. 南京：江苏凤凰教育出版社，２０１７.