重视深度交流 提升数学素养

［摘  要］ 交流是发展学生数学素养的重要途径之一。在小学数学教学中，教师要关注学生的真实想法、真实体验和真实困惑，引导其进行有深度的交流，让学生的思维更有序，发展、提升其学习能力和数学素养。

［关键词］ 交流；深度的交流；数学素养

如何培养和发展小学生的数学素养一直是数学教学的热点话题。培养数学素养的路径有很多，交流是其中之一。交流是教学的“法宝”，通过有层次、有深度的交流，教师可以更好地了解学生，从而促进学生更好地理解知识和深度发展数学思维，提升数学素养。

一、数学交流的现状分析

交流是教师组织教学活动的重要手段之一。通过交流不仅可以活跃课堂气氛，而且可以让学生通过相互启迪明晰解决问题的思路，深化知识的理解，提高思维的条理性和逻辑性。不过，在实际教学中，会因为课堂交流缺乏深度而使交流流于形式，影响了教学质量的提升，限制了学生数学素养的发展。在数学教学中，部分教师对学生开展深度交流的认识还存在一些不足，教学中时常出现“为了交流而交流”的情况，从而使课堂交流失效。

1. 对深度交流认识不足

在实际教学中，数学交流停留在师生交流的层面上，忽视了生生交流的价值。此外，交流的形式单一，课堂交流主要是“师问生答”的形式，学生主动思考、主动探索的意识不强；交流中教师忽视了学生的主体性，限制了学生思维能力的发展和数学素养的提升。

2. 缺少有深度问题的引领

在日常教学中，教师通过主动提问，让学生在问题的引导下去交流、探索、感悟，以便学生更好地理解知识和掌握获取知识的方法。不过，教师习惯于提出“听懂了吗”“对不对”“会不会”等问题，显然这些问题缺乏深度，很难引发学生真正的思考，从而影响交流的效果。因此，教学中教师应关注那些指向数学知识本质的核心问题，以此引发学生深度思考，让数学交流更有效。

二、深度交流的缺失原因

导致课堂深度交流缺失的原因有很多，笔者从教师和学生两个角度进行分析。

1. 从教师角度来看

受传统教学观念的影响，有的教师认为只要按照预设顺利完成教学任务就可以了，没有必要“节外生枝”；有的教师认为小学生知识水平有限，即使开展交流活动也不会发现有价值的信息，而且容易让学生产生畏难情绪，为此课堂教学应以教师为主；有的教师对学生的认知水平把握不够准确，使得问题的创设不适合学生的认识水平而影响参与效果等。基于此，教师应更新教学观念，认真了解学情，准确把握学生的认知心理，以此通过有效问题的创设，引发学生深度思考与交流，有效提升其数学素养。

2. 从学生角度来看

一是在“师讲生听”教学模式影响下，学生对教师产生了依赖，缺乏主动思考、主动交流意识；二是受个体差异的影响，不同的学生认知起点不同，“一刀切”的教学模式会让学生因“吃不饱”或“吃不消”产生消极情绪，影响学生参与课堂的积极性；三是碍于教师的威严，部分学生不敢提出自己的见解、疑惑。可见，学生的“学”还处于一个消极、被动的状态，影响了深度交流的发生。

三、组织深度交流的几点建议

1. 关注真实想法，交流逐步深入

学生作为独立的个体，他们对问题往往有自己独特的见解。教学中，教师要尊重学生，以学生的原有认知为起点，鼓励学生提出自己的想法。当然，学生的想法可能是片面的、肤浅的，甚至是错误的，但这些是他们最真实的看法，也是课堂交流的最佳切入点。在课堂教学中，教师要充分关注学生的真实想法，从学生的角度去思考和解决，逐渐使交流走向深入，逐步抵达问题的核心，揭示问题的本质。

案例1  “圆锥的体积”教学片段

师：结合已有经验想一想，如何求圆锥的体积呢？（教师预留时间让学生思考）

生1：以前研究圆柱体积的时候是将它切开拼成长方体，不知道圆锥行不行。

师：我感觉这个方法行不通，不过我不知道怎么来解释，谁能帮老师解释一下？（学生跃跃欲试）

生2：圆锥和圆柱不同，圆锥上下粗细不同，不能拼成长方体。

生3：我觉得它的计算方法应该和圆柱有关系，它们的底面都是圆形。

师：圆柱的体积是“底面积×高”，求圆锥的体积也能用它来计算吗？

生（齐声答）：不行。

生4：虽然不能直接用“底面积×高”来计算，不过我猜圆锥的体积肯定与底面积和高有关。

师：到底有什么关系呢？

生5：我猜想应该是一半的关系，因为三角形的面积就是四边形面积的一半。

生6：这个不一定成立，接下来应该重点研究圆锥体积与圆柱体积存在怎样的关系。

师：你们觉得它们的体积可能是一半的关系吗？（教师拿出一个较小的圆柱和较大的圆锥让学生观察、辨析）

生7：这个很明显，它们的体积不是一半的关系。我觉得不应该这么比较。

师：你们有更好的办法吗？

生8：如果要比较，应该从“等底等高”的圆柱和圆锥中去观察、分析、比较，这样才能发现它们之间存在的数量关系。

师：你们赞成生8的说法吗？接下来我们需要做什么呢？

从以上教学过程来看，教师没有直接呈现公式让学生练习强化，而是紧紧抓住学生思考问题的最初想法，通过有效问题的引领开展有效的师生和生生交流。教学中，当学生提出将圆锥拼成长方体进行研究，教师明确指出该方法行不通。为了唤起学生的探究欲，教师将“行不通”的理由交给学生来呈现，以此为学生营造了深度交流的氛围。通过逐层深入的思考与交流，学生发现圆锥的体积与圆柱的体积有关系，然后通过探究“两者存在什么关系”这一核心问题，让学生通过观察、联想、实验、辨析等活动直指问题的本质，获得相应的体积计算公式。

教学中，从简单的交流开始，通过师生、生生的有效互动，让不同思维在交流中碰撞出新的思维火花。通过经历知识形成、发展的过程，学生对数学探究过程和特点获得更深层的理解，以此点燃了学生的智慧火花，促进了学生思维发展和学习能力提升。

2. 关注真实困惑，提升思维水平

在学习过程中，学生产生困惑在所难免。教学中，教师要重视呈现学生的思维过程，及时捕捉学生的真实困惑，并结合学生的实际情况组织相应的数学交流，以此通过深度交流消除学生困惑，让学生理解问题的本质，提升学生数学学习能力。

案例2  “小数的近似数”教学片段

通过相关知识的学习，学生能够按照要求写出近似数。教学中，教师给出了这样一个问题：地球与太阳之间的距离大约为1.496亿千米，若将其精确到十分位和百分位，其结果分别是什么呢？学生很快给出答案，其结果依次为“大约1.5亿千米”和“大约1.50亿千米”。答案给出后，教师给出这样一个结论：“1.50”比“1.5”更精确。此结论给出后，不少学生产生困惑，陷入沉思。学生提出疑问：根据小数的基本性质，“1.50”中末尾的“0”是可以去掉的，因此“1.50”和“1.5”是相等的，所以“1.50”比“1.5”更精确这个说法应该是错误的。以上困惑是真实的，而且涉及数学知识的本质，教师决定引导学生一探究竟。

师：比较“1.50”和“1.5”这两个近似值，你们有什么想说的吗？

生1：它们两个是相等的，因为“1.50”中末尾的“0”是可以去掉的。

生2：0不能去掉，去掉其意义就变了，它就不能表示“精确到百分位”的数了。

师：生2的说法很有道理，因为这里“1.50”和“1.5”是近似数，一旦去掉“1.50”后面的0，它所表示的精准程度就不一样了。谁来说一说，对于“精准程度”你们是如何理解的？

生3：就拿“1.50”和“1.5”来分析，前者是精准到百分位的近似数，后者是精准到十分位的近似数，它们的精准程度不同。

师：分析得很有道理。现在请大家思考这样一个问题，一个两位小数精准到十分位其近似值是“1.5”，那么这个两位小数最大是多少？最小是多少呢？

生4：最大是1.54，最小是1.45。

师：非常好，如果一个三位小数精准到百分位其近似值为“1.50”，那么这个三位小数最大是多少？最小又是多少呢？

生5：分别为1.504和1.495。

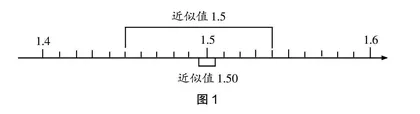
师：非常好，现在我将以上结果用图1演示，你们有什么发现？（教师课件出示图1）

生6：两个近似数所对应的小数范围不一样，范围越小表示它越准确，所以近似数1.50更精准。

师：现在你们认为近似数“1.50”中的“0”还能去掉吗？

教学中，教师及时捕捉学生的真实困惑，以学生的真实困惑“近似数1.50比近似数1.5更精确”为交流焦点，让学生通过交流发现“近似数1.50与近似数1.5”的精确程度是不一样的，所以不能去掉“0”。为了进一步深化理解，教师继续让学生思考“近似数1.50”和“近似数1.5”表示范围，由此借助图形的直观进一步明晰两者的区别，理解问题的本质。

在面对抽象的数学知识时，已有认知和新知难免会出现矛盾，教师要抓住这些“矛盾”，引导学生进行深层次的思考与交流，让学生既能深刻理解知识，又能感受数学的严谨性。

3. 关注真实差异，拓展交流空间

学生在思考和解决问题时，通常从自己熟悉的角度分析，选择自己擅长的方式去解决。学生的认知能力、思维方式、生活经验等存在差异，因此他们思考和解决问题的方式有所不同。教学中，教师既要尊重差异，又要合理利用差异。这样不仅可以拓展学生的交流空间，还能帮助学生积累丰富的交流经验，提升数学素养。

案例3  “除数是整数的小数除法”教学片段

教师出示练习：小明买了3支同样的笔共花费7.2元，问每支笔多少钱？

问题给出后，教师先让学生独自探究计算方法，然后组织学生合作交流。

师：谁来说一说计算结果是什么？你是如何计算的呢？

生1：我把7.2元看成72角，求得每支笔24角，就是2.4元。

师：非常不错的想法，通过等价转化解决了问题。还有其他方法吗？

生2：我是把7.2分成了6和1.2，6÷3=2，1.2÷3=0.4，合起来是2.4。

师：1.2÷3=0.4？你是怎么想的呢？

生2：12除以3等于4，所以12个0.1除以3就是4个0.1，就是0.4。

师：按照你的说法，0.12÷3=？

生2：4个0.01，就是0.04。

师：还有其他不一样的计算方法吗？

生3：可以先算72除以3，72除以3得24，所以72个0.1除以3，就是24个0.1，也就是2.4。

师：我是这样算的。（教师给出竖式计算过程，如图2）

师：结合刚刚的讨论，以上竖式可以如何理解呢？

生：（回答略）。

在以上探究活动中，教师鼓励学生从自己的已有知识和已有经验出发，先自主探索小数除以整数的计算方法，然后提供机会让学生表达自己的看法与见解，让不同思维在交流中碰撞出火花，以此让学生掌握计算方法和理解算法背后的计算原理，从而认清数学的本质。

4. 重视反思归纳，提升交流能力

反思归纳是数学教学的重要一环，是升华学生认知、提升学生数学素养的必经之路。教学中，教师要提供机会让学生回头看，通过有效的梳理和反思帮助学生将知识内化为能力，促进学生数学交流能力的提升。

案例4  如图3，比较两个图形面积的大小。

问题给出后，学生运用转化策略将图形转化为熟悉的长方形，从而判断两个图形的面积相等。问题解决后，教师给出如下问题让学生思考、交流：

（1）解决该题最关键的环节是什么？

（2）你是如何将它们分别转化成长方形的？

（3）是不是复杂图形都可以转化为相对简单的长方形呢？

（4）这种转化策略之前是否应用过？如果应用过，请举例说明。

通过以上问题的引导，学生进一步思考和交流，以此建构完善的认知。教学的目的不是简单地让学生解决问题，而是让学生获得自己解决问题的能力。因此，在整理反思有关的交流活动时，教师要有意识地引导学生多问“为什么”，比如“为什么要这样做”“还能怎么做”“还有什么疑问和困惑”等，让学生通过深层交流更好地理解知识与方法，提升学生交流能力和数学素养。

总之，教师要重视学生内隐的真实想法、体验、困惑，善于结合教学实际提出有深度的问题，从而让学生在有深度的问题引导下，通过经历思考、交流、反思等过程，更好地理解知识、提升技能和发展数学素养。