经历探究过程，培养转化思想

［摘  要］ 研究者以“多边形的面积”单元开启课“数图形的面积”为例，通过“复习旧知，揭示课题；自主探究，合作交流；课堂小结，回顾方法”等教学活动，让学生经历探究过程，培养学生的转化思想。

［关键词］ 转化思想；单元开启课；多边形的面积转化思想也叫化归思想，是重要的数学思想方法之一。转化思想是将一个问题由难化易、由繁化简的过程。在小学数学教学中教师要引导学生运用转化思想，比如，将两位数乘两位数的竖式计算转化为两位数乘一位数的竖式计算；通过具体的例子发现运算定律后用字母式来表示；解决几何问题时进行数与形的转化。

笔者在教学“多边形的面积”单元开启课时，引导学生运用转化思想探究平行四边形、三角形、梯形和不规则图形的面积，将多边形转化为学生已经学过的长方形或正方形，从而培养学生的转化思想。

一、课前思考

“多边形的面积”单元属于新课标中“图形与几何”领域中“测量与计算”的教学内容，图形的测量和计算是空间观念形成的载体，学习这部分数学知识的重要价值在于培养学生的空间观念和空间想象力。“测量与计算”的教学内容分布在教材的不同年级中，“多边形的面积”单元的教学重点是转化思想的运用，让学生经历长方形面积公式的推导过程，将未知图形的面积转化为已知图形的面积进行计算。

苏教版小学数学教材中的“多边形的面积”单元的课时编排是这样的：平行四边形的面积（2课时）、三角形的面积（2课时）、梯形的面积（2课时）、认识公顷和平方千米（1课时）、简单组合图形的面积（1课时）和不规则图形的面积（1课时）等。笔者对本单元的教学内容进行了重组：数图形的面积（1课时）、平行四边形的面积（1课时）、三角形的面积（1课时）、梯形的面积（1课时）、面积练习课（1课时）、认识公顷和平方千米（1课时）、简单组合图形的面积（1课时）、不规则图形的面积（1课时）和单元复习课（1课时）等。

二、教学实践与思考

基于对转化思想的理解，笔者确定“多边形的面积”单元开启课“数图形的面积”的教学目标：（1）让学生通过对图形面积的研究，加深对面积含义的理解；（2）让学生在数各种平面图形面积的过程中能把这些图形转化为长方形或正方形等规则图形，掌握割补法、倍拼法等转化方法；（3）让学生在解决几何面积问题过程中积累数学活动经验，培养转化意识。

1. 复习旧知，揭示课题

师：（出示边长是1厘米的小正方形）同学们，这个小正方形的面积还记得吗？

生（齐声答）：1平方厘米。

师：（出示一个长方形）如果我们要知道这个长方形的面积，你们会怎么做？

生1：先数长方形的长边有几个这样的1平方厘米的小正方形，再数长方形的宽边有几个这样的1平方厘米的小正方形，最后把长边小正方形的个数乘宽边小正方形的个数就是长方形的面积。这个长方形的长边有5个1平方厘米的小正方形，宽边有3个1平方厘米的小正方形，所以长方形的面积是15平方厘米。

师：我们可以用数面积单位的方法计算图形的面积。（出示一个正方形）请你们算一算这个正方形的面积。

生2：这个正方形的边有4个这样的1平方厘米的小正方形，所以正方形的面积是16平方厘米。

教学思考：学生在三年级时认识了面积和常见的面积单位，能用数面积单位的方法探究长方形和正方形的面积。在课堂伊始，教师先引导学生复习常见的面积单位，然后让学生通过面积的含义回顾长方形和正方形面积公式的推导过程。

2. 自主探究，合作交流

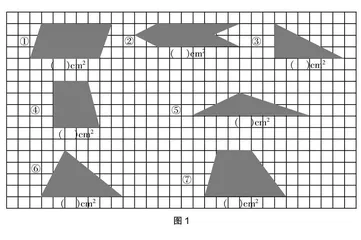
师：如图1，这里每个小正方形的面积是1平方厘米，你们能想办法计算这些平面图形的面积吗？先独立思考并完成学习单，然后在四人小组里交流。

生3：第一个图形是平行四边形，我先把右边的三角形剪下来拼到左边，这样就变成了长有6个1平方厘米、宽有3个1平方厘米的长方形，这个长方形的面积是18平方厘米，所以这个平行四边形的面积是18平方厘米。

师：这位同学把右边的三角形移动到左边，仔细看一看拼好后是不是一个长方形？

生（齐声答）：是。

师：（总结）我们要确保转化前的平行四边形面积和转化后的长方形面积保持不变。

生4：我把第二个图形左边的三角形移动到右边，正好变成长是7厘米、宽是2厘米的长方形，所以第二个图形的面积是14平方厘米。第三个图形是三角形，我把上半部分的三角形拼到下面就变成了一个长方形，它的面积是9平方厘米。

生5：我有补充，我可以再补一个完全一样的三角形，这样就变成了一个长是6厘米、宽是3厘米的长方形。因为这个长方形的面积是18平方厘米，这个三角形面积是长方形面积的一半，所以这个三角形的面积是9平方厘米。

师：生4是把上面的三角形移动到下面，补成一个长方形，这种方法叫作割补法；生5用两个完全相同的三角形拼成了一个长方形，三角形面积是长方形面积的一半，这种方法叫作倍拼法。

生6：第四个图形是梯形，我是把上面半个梯形旋转后拼到下面，这样就变成了长是7厘米、宽是2厘米的长方形，转化后长方形的面积是14平方厘米，所以这个梯形的面积是14平方厘米。第五个图形是钝角三角形，把左上角的三角形旋转下来，把右上角的三角形旋转下来，这样就变成了长是10厘米、宽是1厘米的长方形，所以这个三角形的面积是10平方厘米。

教学思考：在这个教学环节中，教师有目的地精选了七个典型的平面图形：平行四边形、不规则图形、直角三角形、直角梯形、钝角三角形、锐角三角形和普通梯形，这些平面图形都是本单元学生要学习的内容。教师让学生在探究中初步掌握用割补法和倍拼法把各种平面图形转化为长方形或正方形。

3. 课堂小结，回顾方法

师：同学们，回顾一下我们是怎么数出这些图形面积的？我们用到割补法和倍拼法，把未知图形的面积转化为我们已知图形的面积。割补法与中国古代数学家刘徽在《九章算术》中的“出入相补”非常相似，你们知道什么是“出入相补”吗？我们一起来看一个小视频。

师：同学们，通过观看这个小视频，你们学到了什么？

生7：一个几何图形可以被切割成任意数量或任意形状的小图形，总面积或体积保持不变，等于所有小图形的面积或体积之和。一个几何图形可以任意旋转、移动和复制，不改变其面积或体积的大小。多个几何图形可以任意组合，总面积或体积保持不变。

师：同学们，这样的转化在我们以后的学习中还会有更多的用途。

教学思考：在这个教学环节中，教师带领全班学生回顾了这节课的学习过程，总结了割补法和倍拼法在平面图形转化中的作用。教师还向学生介绍了中国数学家刘徽的“出入相补”与割补法的原理类似，都是把几何图形进行切割、旋转、移动、复制和组合，转化后的总面积和总体积与原来的总面积和总体积保持不变。

综上所述，教师在七个平面图形的面积计算的教学中，引导学生从平面图形面积度量的本质出发，通过对多边形进行图形的转化、迁移和类比，让学生积累数学活动经验和发展数学转化思想，真正提升了学生的探究能力和数学素养。