SOLO分类理论在小学数学教学中的实践研究

［摘  要］ SOLO分类理论将学习者的思维层次从低到高分成前结构、单点结构、多点结构、关联结构和抽象拓展结构五个层次。研究者以学生解一道“不规则物体的体积”的问题为例，从研究的缘起、理论概述、分层分析和教学启示四个方面展开分析。

［关键词］ SOLO分类；不规则物体体积；教学《义务教育数学课程标准（2022年版）》强调：评价不仅要关注学生数学学习结果，还要关注学生数学学习过程，激励学生学习，改进教师教学。“图形与几何”是小学数学课程的重要组成部分，对发展学生的数学思维与空间观具有重要价值与意义。

一、研究的缘起

在一次数学检测中笔者发现学生对“图形与几何”部分“求不规则物体的体积”的正确率仅有40%左右。为此，笔者深入剖析错因，以探寻解决问题的策略。

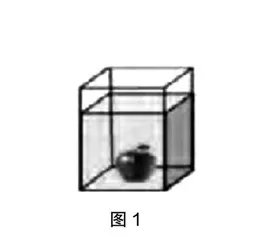
原题：如图1，向一个底面积为2.5平方分米的长方体容器内倒入3.5升的水之后再放入1个苹果，苹果完全沉入水底后水面上升到17厘米，且没有水溢出容器，求该苹果的体积。

图1

试题分析：此题以图文方式呈现，图的应用是为了唤醒学生对求不规则物体体积的记忆，笔者在学生以前的练习题中找到了本题的原型。

原型习题：向一个底面边长为2分米的正方体容器内倒入5升水之后再扔一块不规则的铁块进去，此时水没有溢出，水的高度为20厘米，求铁块的体积。

这两道题惊人的相似，问题的条件与待求问题都差不多，两题的异同点见表1。

通过对教材与学生以前的练习题的梳理，发现共有11道类似求不规则物体体积的问题。从这一点来看，学生对本题有一定的经验基础。但是实际检测结果不尽如人意，究竟是哪个环节出现了问题呢？为了追根溯源，笔者决定抽取一定的检测样本，借助SOLO分类理论进行分析与研究。

二、SOLO分类理论概述

SOLO分类理论是一种以等级描述为特征、对学生学习成效进行评价的方法，将学习者的思维层次从低到高分成五个层次，分别为：前结构、单点结构、多点结构、关联结构和抽象拓展结构。

从SOLO分类理论的分层情况来看，它体现的是学生思维循序渐进发展的过程，对评价学生的思维水平具有直接意义。前三个层次主要反映的是学生对基础知识的理解与掌握情况，后面两个层次则表现了学生思维的飞跃。结构越复杂对应的思维层次就越高，因此，这是一种能够有效评价学生思维发展程度的理论，对促进学生学习能力发展具有重要意义。

三、分层分析学生的作答情况

笔者将参与测试的223人视为整体，结合SOLO分类理论分别从学生的思维层次、整体答题情况等方面分析学生的认知水平。

1. 作答结果分析

完全正确59人，约占总人数的26.5%；解题思路正确，但单位换算或计算错误有21人，约占总人数的9.4%；完全错误有143人，约占总人数的64.1%。这组数据真实反映了学生的实际答题情况（见表2）。

观察表2可知，学生计算不规则物体体积问题的能力非常弱，其中出现计算错误、单位错误、数据抄错等问题的学生不少，由此可以看出学生的基础知识掌握不扎实。超过40%的学生对解题策略完全没有理解与掌握。

2. 思维层次分析

以上数据大致反映了学生存在的问题，为了进一步深入了解学生的思维水平，笔者借助SOLO分类理论对学生的思维结构与认知水平进行分析，明确学生的错误原因，为精准采取应对措施奠定基础。SOLO分类理论有助于教师对学生的学习质量进行客观、深入分析与评价。

从SOLO分类理论的五种思维水平层次描述与划分的角度出发，笔者对学生求不规则物体体积问题的思维层次进行了深入统计与梳理，结果见表3。

将表3中呈现的数据和学生认知水平进行关联，形成统计图（图2）。观察图2，学生的思维水平的分布呈现高低起伏状态，由此可以判断学生对于计算不规则物体体积问题的思维大多处于单点结构水平，占到本次参考总人数的48.5%，这个数据反映近一半的学生对这类问题的认知处于操作性记忆水平；多点结构占本次参考总人数的9.4%，抽象拓展结构水平的学生人数是关联结构水平人数的3倍多。这些数据显示学生的思维水平出现严重的两极分化现象。

为什么会出现这种情况呢？究其原因主要有：①一些学生无法从真正意义上理解题意，没有理解题设条件中的“上升到”的实际意义；②一些学生无法将苹果体积与上升水位的体积等同起来；③部分学生无法自主获取题设条件中的关联信息，对于此类问题的解题策略缺乏理解。

3. 典型作答分析

在宏观角度分析的基础上，笔者择取了各水平层次学生的典型作答情况，并进行了思维水平的深层次剖析。

（1）前结构水平

该水平层次的学生呈现的解题状态为完全不会，试卷呈现为空白或答非所问的解题过程。具体来说，有13份试卷呈现空白状态，这些反映学生没有进入学习状态，没有动脑筋分析与解决问题；有22份试卷呈现“胡乱作答”的情况，这些现象说明学生根本没有掌握基本的解题思路与方法，完全不理解这一类问题。

（2）单点结构水平

处于此水平的学生人数较多，统计发现共有57名学生用底面积乘以高2.5×17之后，将结论乘以3.5进行解题。从这个解题思路来看，学生并没有理解题设条件中的信息关系；有51人的错误解题过程为：17cm=1.7dm，2.5×1.7=4.25dm2。从这个解题方法来看，学生对“上升到”与“上升了”的理解不清晰，虽然他们知道体积公式，但是没有充分理解题意，无法正确解题。这两种典型错解方法体现了这部分学生对于信息的理解呈现点状结构。

（3）多点结构水平

一部分学生虽然能处理多个信息点，但是对信息的关联无法准确处理。最典型的错误类型分别有：①17cm=1.7dm，3.5L=3.5dm3，2.5×1.7-3.5=0.65dm3；②3.5÷2.5=1.4dm=14cm，2.5×（17-14）=7.5cm3。统计发现有11人采用错误①的方法解题，有8人出现错误②的单位换算问题。此类答题模式显示这部分学生虽然明白要进行体积转换来解决问题，但是运算与单位换算的能力欠缺，无法将运算与单位换算形成关联，导致解题错误。

（4）关联结构水平

该水平层次的学生能将多个信息点成功关联，进行正确解题。统计发现共有14名学生能准确列式、运算，并完整地写出答语，典型解题方法有：17cm=1.7dm，2.5×1.7=4.25升，4.25-3.5=0.75dm3。学生通过对题设条件的正确解读、理解，能获得正确结论。

（5）抽象拓展结构水平

分析学生的解题情况，处于该阶段的学生可自主进行数学抽象，能灵活应用解题策略操作，并让解题保持开放性。学生典型解题方法有两类：①3.5L=3.5dm3，2.5dm2=250cm2， 3.5÷2.5=1.4dm=14cm，（17-14）×250=750cm3；②3.5L=3.5dm3，3.5÷2.5=1.4dm， 17cm=1.7dm，1.7-1.4=0.3dm，0.3×2.5=0.75dm3。

统计发现有45名学生采用了以上两种解题方法，这部分学生已经能够自主抽象出“不规则物体的体积=底面积×高”的模型，并能灵活应用在解决实际问题中。这属于抽象拓展结构水平阶段，能彰显学生具有深度理解、自主建构的学习能力。

四、SOLO分类理论应用指导

通过SOLO分类理论诊断与分析学生的解题情况和认知水平，从分析过程中可以看出SOLO分类理论能够对学生的认知水平形成客观、公正、科学的判断，为接下来的教学提供明确的依据。

1. 精准测评学力，利于分层指导

对学生作答的思维水平用SOLO分类理论进行分层统计与分析，教师可以精准发现学生对于此类问题在理解能力上的显著差异。从统计结论来看，有一部分学生完全不理解这一类问题的解题思路，纯粹胡乱答题，针对这种情况，教师要给这部分学生“开小灶”，进行解题策略的引导，以达到补救的目的；对于解题思路正确、单位换算与计算错误的这部分学生，教师要针对性地进行单位换算与计算训练，以达到查漏补缺的作用；对于一些既不会做、又不想做的学生，教师要关注他们的学习态度，对其进行访谈、心理引导、激趣启思等。

2. 明确教学缺失，便于跟进弥补

通过对学生解题情况的分析，教师发现不少学生在解决关于不规则物体体积问题时，用得较多的方法并不是常规的“总体积-原体积”，而是“底面积×高”来获得不规则物品的体积。处于单点结构水平与多点结构水平的学生都呈现这种解法，由此基本能判断教师在授课时缺失对于“底面积×高”模型的教学。因此，教师应及时反思自己的教学，根据本次分析情况及时调整教学方案。

基于实际思维水平层级情况来看，学生能理解用“底面积×高”策略来解决此类问题。因此，实际教学中，教师要加强学生对“底面积×高”模型的构建，让学生充分理解求规则物体体积与不规则物体体积的本质是一致的。

3. 明确提出建议，用于精准实施

根据SOLO分类理论的分析，为教师在图形与几何领域中的测量部分教学提供了一定的启示：①要充分重视学生测量概念的形成过程，比如对物体的周长、面积与体积的度量、单位等要有理性的认识；②要关注学生的操作体验，引导学生在自主实践中理解并掌握知识与技能关联的实际意义，如感知物品“叠加”过程，提高操作性理解等；③要加强实验探究，关于测量的实验素材有排水法、测沙法等，学生只要亲历实验过程就能构建探究性的理解，提升认知水平。

总之，SOLO分类理论的应用，让教师清晰地发现学生对同一问题的不同理解水平，给教学的实施带来很多启发。SOLO分类理论是一种指向学生数学理解能力的评价手段，对促进学生深度学习具有重要价值与意义。