“为深刻理解而教”的内涵、价值与教学路径重构

［摘  要］ 数学深刻理解涉及深层次的认知过程和知识应用，指向结构化理解以及更高的文化感悟与理解，具有真实性、可视化、可迁移、自调控等特征。在小学数学教学中，教师可以通过关注情境、关联结构、有效迁移、充分反省、注重评价等教学路径让学生深刻理解数学内容。

［关键词］ 小学数学；深刻理解；情境；结构；迁移

当下，数学教育领域涌现许多有研究价值的理念，如“深度学习”“学为中心”“结构化教学”等，这些教育教学理念都和“深刻理解”有紧密的联系。深刻理解的核心就是教师要为学生的可持续发展提供支点，支持学生进行和谐、个性、快乐、有意义的学习。“数学深刻理解”的本质是一个涉及知识获取、应用和深层次认知过程的复杂现象，它不仅包括对数学事实、概念、原理和方法的理解，还涉及对数学本质、数学思想方法的探索和认识。数学理解的过程是多层次、多维度的，学生需要通过不断实践和反思来深化与拓展。学生只有深刻理解学习内容，才能掌握数学思想方法和提升解决问题的能力。“深刻理解”更加关注培养学生的理性精神和思维品质，为数学教育教学提供一种全新的视角。

一、“数学深刻理解”的内涵与特征剖析

1. 相关概念的解析

（1）“理解”的内涵

在厘清什么是“数学深刻理解”之前要思考什么是“理解”。“理解”是一个多维度的通识概念，涉及心理学、教育学、哲学等多个领域。从心理学的角度来看，“理解”被看作是一种心理活动的过程，涉及对言语和行动意义的理解［１］；从教育学的角度看，“理解”是学习者认知结构的建构和知识意义的建构，它不仅指向学习结果，更是一种处于不断迭代、发展的过程。有人将理解划分为不同的层次，如了解、领会、掌握、熟练运用等，认为是否能进行“迁移”是理解的表征。无论如何，“理解”要以可视化的表现作为评定标准。“理解”既有助于学生完善已有的知识结构、认知结构、方法结构和思维结构，又便于建构、同化新的学习对象，这是一个双向促进的良性循环的学习过程。

（2）“数学理解”的内涵

“数学理解”的内涵涉及知识的建构、应用和创新，它不仅是对数学知识的记忆和重复，更是一种深层次的认知活动，涉及认知过程与结果的相互融合。“数学理解”以数学知识的结构化、网络化和丰富联系为本质，以生成性和发展性为特征，以重新组织为形成机制，以自主活动为形成条件［２］。“数学理解”是一个不断调整、分层次、非线性发展的过程，建立在学生已有的知识结构和认识结构之上，学生将新获取的外部信息主动与已有信息进行不断交互，从而形成构建新知、获取新经验的认知活动。

“数学理解”包括对数学概念、性质、法则等方面的全面性把握。数学概念具有抽象性，这是数学的本质特征之一，这种抽象性不仅体现在数学概念的形成过程中，也体现在数学知识的构建和应用中。因此，教师要引导学生站在结构化、整体化、系统化的视角去构建知识体系。这涉及数学理解过程的多样性、抽象性、系统性，这种理解不仅是对数学符号的记忆，而且能够深入数学概念的本质，把握其内在逻辑和应用范围。“数学理解”的多样性不仅包括对数学概念、知识和技能的不同层次的理解，还包括教学方法和策略的多样化，以及经验性理解、概念性理解和操作性理解。

（3）“数学深刻理解”的内涵

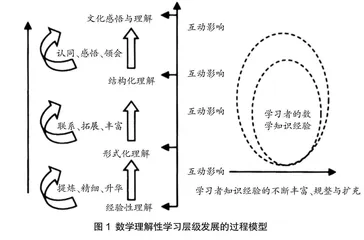
事实上，“数学理解”涉及知识的层次性，包括零层次、常识性层次、逻辑性层次、观念性层次等［３］。这些层次反映了数学理解的不同深度和广度，从直观理解到抽象理解，再到创新性理解，每个层次都要求学生在前一个层次的基础上进行深化和拓展。如图1，理解性学习具有明显的层级特征［４］。

数学课堂追求的是“深刻理解”。“数学深刻理解”是在浅层次理解的基础上进一步深化，它已经超越了经验性理解和形式化理解。“数学深刻理解”涉及更深层次的认知过程和知识应用，指向结构化理解以及更高的文化感悟与理解。“数学深刻理解”是学生在对数学概念、性质、法则的接收、处理和记忆的基础上，经历横向数学化与纵向数学化的过程，完成知识之间关联的构建以及跨学科的学习，这种全方位的学习过程有助于学生构建更加全面和系统的认知结构。因此，“数学深刻理解”是指学生在真实情境中通过问题解决体现知识网络的社会建构性、关联结构性和主体参与性，进而形成批判性思考和创造性应用［５］。数学不是一门静态的学科，它的应用是动态变化的。“深刻理解”的达成有助于学生用数学的眼光去解决复杂情境中的实际问题，让学生借助实践和应用进一步加深对数学概念的理解。

2. “数学深刻理解”的特征

（1）真实性——以“真实情境”唤醒已有经验

“数学深刻理解”的特征之一是具备真实性的问题情境，“真实性”是数学核心素养的关键要素之一。在实际教学情境中，部分学生只是在某个单元学习过程中才能学会相对应的知识，一旦跳出单元或者学科的框架，这些知识则难以被激活，像这样的知识被称为“惰性知识”。“深刻理解”强调真实情境，是为了唤醒学生的“惰性知识”。教师通过开放性问题或情境模拟，让学生在解决问题的过程中深入探索、理解和应用知识点，引发学生对已有知识和新知识之间的关系进行思考，从而促进“深刻理解”的发生。“数学深刻理解”意味着学生能够灵活运用相关知识和活动经验、生活经验进行迁移和应用，“深刻理解”不仅是“知”，还要能“做”，“知行合一”才是真正的理解。

（2）可视化——以“认知图式”作为心理依托

学生在学习一个新的数学概念时，需要调动相关联的已有知识和经验，借助图式表征对新概念进行拆解与重构，进而实现思维的可视化，展现不同学生所处的认知水平。借助“认知图式”在一定程度上能让学生避免知识学习的碎片化、零散化，如“思维导图”帮助学生建立知识间的联系和厘清知识脉络，“数学深刻理解”往往通过应用数学认知图式促进学生对数学概念的深刻理解。

（3）可迁移——以“专家思维”解决实际问题

“高通路迁移”是指学生能够将所学知识从具体情境中抽象出来，并应用于新的、未接触过的情境中。这种迁移不是简单的知识复制或重复，而是学生在“数学深刻理解”的基础上进行创新性的思考和应用。“数学深刻理解”是否达成的表征之一就是观察学生的学习过程是否能够产生“高通路迁移”和形成专家型思维，是否能够将抽象的知识具体化，创造性地利用所学知识解决新的问题。

（4）自调控——以“评价反思”优化认知结构

“深刻理解”的数学课堂是能够体现“教—学—评”一致性的新型课堂。“反馈”作为一个教育心理学的重要概念，是保障学生学习活动得以真正发生的重要手段。评价的出发点和落脚点是促进学生的可持续发展。这种“反馈性”体现在学生了解评价目标、评价任务中自身表现与高水平表现之间的差距以及对于出现的差距进行有效调控等。

其实，学生在完成评价任务的过程中已经自主实现“可理解性”的学习，厘清数学知识的来龙去脉，逐步构建知识网络。教师要以“数学深刻理解”为目标，以评价为媒介，以数学素养提升为追求，全面提升学生的元认知水平，推动其理解过程逐步生动化、全面化、系统化，使学生的数学理解真实且深刻。

二、“数学深刻理解”的价值追寻

1. 学生高阶思维发展的“生长点”

学生在对数学概念、性质、法则等学习对象进行初步感知、建立表象的过程中，其思维得到不同程度的发展，“数学深刻理解”格外关注高阶思维形成的路径。高阶思维包含问题的发现与解决能力、创造性思维、批判性思维和元认知能力等重要组成部分，“数学深刻理解”对于学生高阶思维的培养具有重要意义。“问题”的发现、提出、探究与解决贯穿高阶思维活动的全过程，问题解决的过程处处体现着思维的深刻性，这是高阶思维不断发展、完善的不竭动力。此外，几乎所有的数学思想、方法都渗透在学生深刻理解的认知过程之中，数学学习不仅是知识与技能的习得，更是学科素养的提升与发展。

2. 学生理解学科大概念的“触发点”

“大概念”是居于学科核心地位的具有统领性的概念，其提取过程伴随着学生对数学概念的深刻理解，因为只有深刻理解才能实现知识间的关联与融通，才能实现认知的建构与优化，在知识结构与认知结构的形成过程中大概念才有可能从若干点状的知识中被提炼出来。学科大概念具有一定的抽象性、概括性，因此围绕大概念进行学习会激发学生一系列的知识和经验，大概念的探究性习得的过程自然地伴随着学科知识结构化、网络化的过程。在这个过程中，学生对新知的理解以及新知和已有知识结构进行相互作用，不断呈现为表征、图示、同化、顺应和平衡的形态。

3. 学生核心素养形成的“延伸点”

浅层学习是指学生所习得的是“惰性知识”，它们不能在有关学科情境或者生活情境中被有效激活。在实际教学中，学生仅靠机械记忆所获取的概念、定理等内容大部分都属于“惰性知识”，因为这些知识未能在学生的头脑中进行深层次加工。在“素养本位”的价值追求引领下，教师应引导学生进行深刻思考，开展深层学习。学生只有经过深刻的数学思考过程，“惰性知识”才能被激活。创造性地应用知识是素养形成的重要标志，因此，“数学深刻理解”是核心素养培育的重要手段。

三、小学数学教学中学生深刻理解的路径探寻

1. 关注情境，为学生深刻理解筑牢“四基”

《义务教育数学课程标准（2022年版）》指出：注重发挥问题情境对学生主动参与教学活动的促进作用，使学生在活动中逐步发展核心素养。近年来，创设问题情境得到越来越多教师的关注，问题情境能缩短学生已有的认知经验、生活经验与数学本身的距离。在实际教学中，创设问题情境时教师常常聚焦于知识层面的认识与理解，无法为促进学生的自主建构、达成数学理解搭建阶梯。问题情境分为情境指向与问题指向两种视角，其中情境指向观照于学生的学习环境、心理环境以及课堂情境，问题指向则认为问题情境更多是一种数学任务或者数学实作，“理解一个主题”就是利用这个主题进行弹性实作［６］。

基于深刻理解的问题情境创设要将情境指向与问题指向进行有机整合，既关注问题情境的“真实性”特征，通过问题情境将学生的数学知识与已有的数学知识、跨学科知识以及生活经验进行链接关联，又关注问题情境的“思考性”特征，通过完成数学任务与数学实作，形成对数学知识的深刻理解。

（1）冲突性思维情境激发学生深刻理解的内在需求

英国学者巴雷尔认为：“内涵丰富、值得持续思考、富有教育意义、具有启发性的问题情境才是最好的问题情境。”创设冲突性的情境能够有效激发学生的内在需求。值得注意的是，教学情境中的“冲突”不是教师人为创设的“陷阱”，而是学生在已有认知基础上所产生的一种原始想法与真实迷思，教师引导学生直面真实困惑，放慢知识的构建速度，能逐步突破思维困境。

比如在教学“异分母分数的加减法”时，笔者为学生提供了正方形纸片、长方形纸片、线段图以及空白纸片等多项素材计算■+■，部分学生受整数加法负迁移的影响，直接用分母加分母、分子加分子，得到了分数的和是■。因此，教师可以借助图形引发认知冲突，让学生感受分数加法与整数加法的不同之处。教师不可回避学生的原始错误，要在冲突与辨析中引导学生逐步深入理解。

（2）层次性学习情境关注差异化表达

苏联心理学家维果茨基认为学生的发展有两种水平，一种是学生的已有水平，一种是学生可能的发展水平，两者之间的差异就是最近发展区。研究者将情境分为准现实情境、准数学化情境和数学化情境三个层次，通过不同层次的情境引导不同水平的学生形成对问题的个性化理解，缩短学生达成深刻理解的“潜在距离”，从而实现数学的深刻理解。准现实情境是通过对情境的描述或者示意图、图形等形式将现实生活中的情境呈现给学生；准数学情境包含两种不同范畴的元素，既有生活化的元素，又有数学化的元素。数学化的情境则是来源于数学内部的抽象化情境。问题情境的层次性要求教师在情境的设计时应关注不同层次学生的已有水平以及学生之间的“潜在距离”，通过不同层次的任务引导不同水平的学生实现“最近发展区”的跨越。