精心设计数学问题，促进学生思维发展

[摘  要] 问题是数学思维远航的起点和动力，教师应基于学情和教学内容，精心设计数学问题，促使学生积极思考，主动探究。唯有如此，才能让学生的数学思维走向理性，走向深刻。

[关键词] 数学问题;思维发展;教学设计

发展学生的数学思维，离不开高品质问题的支撑，富有探究价值的问题能够引发学生自主探究的欲望，提升学生积极的情感体验，激发学生深层次的认知参与[1]。在教学实践中，教师应该如何设计问题？

一、设计挑战性问题，启动思维

问题是启动学生思维的“引擎”。教师应结合教材内容，立足于学生的最近发展区，设计既让学生感到似曾相识，又无法轻松解决的具有一定挑战性的问题，进而引发学生主动思考，点燃学生思考热情。

（一）引发认知冲突，激活思维因子

设计具有挑战性的问题，打破学生原有的认知平衡，引发学生认知冲突，可将学生置于一种“心求通而未得之意，口欲言而未能之貌”的“愤悱”状态，从而有效驱动学生的思维。

比如，在讲到“圆的周长”时，教师设计问题：小蚂蚁和小蜗牛进行跑步比赛，小蚂蚁沿着正方形路线跑，小蜗牛沿着圆形路线跑。正方形的边长是1米，圆形的直径是1米，它们跑一圈用的时间相同。谁跑的速度更快？

生1：小蚂蚁和小蜗牛跑一圈用的时间相同，那么谁跑的距离远，谁的速度就快。

生2：正方形的周长=边长×4=1×4=4（米），小蚂蚁跑了4米。

师：小蜗牛跑的路线是圆形，圆形的周长怎么计算呢？

生3：圆形是由曲线围成的，我们不能用直尺直接测量出它的周长。

（学生讨论。）

生1：用带子绕圆一周，去掉多余的部分，测量出带子的长度就是圆的周长。

生2：我们还可以将圆在直尺上滚动一周，从直尺的0刻度到滚动一周的终点，这就是圆的周长。

师：缠绕法和滚动法都是利用了化曲为直的思想。但是，如果让你测量摩天轮的周长，还能用这两种方法吗？

生3：不能，摩天轮太大了，这两种方法用起来很不方便。

师：缠绕法和滚动法都具有局限性。看来我们还需要探究一种更具普遍性的圆的周长的计算方法。

由于直尺不能直接测量圆的周长，这就激发了学生的认知冲突，促使学生主动地思考问题。当学生运用缠绕法和滚动法测量出圆的周长后，教师要求学生测量摩天轮的周长，这再次激发了学生的思维冲突，使学生认识到缠绕法和滚动法的不足之处，从而产生了进一步探究的内在需求，激活了学生的思维因子。

（二）设计开放性问题，点燃思维火花

真正的“好问题”应该具有一定的开放性，使各个层次的学生都有机会主动参与学习中。在设计问题时，不仅要围绕教学目标，还应该使问题具有开放性，发展学生思维的创造性。

比如，在讲到“多边形的面积”时，教师设计问题：

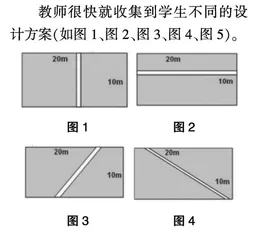
有一个长为20米、宽为10米的长方形草坪，在对边之间修一条1米宽的笔直小路。请你设计一下，这条路可以怎样修？剩下草坪的面积是多少呢？

（学生设计，并展开交流。）

教师很快就收集到学生不同的设计方案（如图1、图2、图3、图4、图5）。

在此基础上，教师进一步提出问题：哪种设计方案剩下的草坪面积最大？请同学们展示自己的计算过程。

学生通过分析得知，图1中小路的面积是1×10=10（平方米）;图2、图3、图4、图5中小路的面积都大于1×10=10（平方米）。所以，图1这种设计方案剩下的草坪面积最大。

教学中，教师设计具有开放性的“问题场”，不同层次、不同思维方式的学生都能设计出一种或几种问题解决方案，学生真正成为学习的主人。

二、设计核心性问题，推动思维

在问题设计中，教师要精准把握知识的本质和结构，有效提炼出核心性问题，从而将学生的思维推向更深、更广的层面[2]。

（一）递进式“问题串”，拓展思维深度

学习的过程是一个层层递进、不断完善的自我建构过程。教师应结合知识的递进性和思维的逻辑性，设计出由浅入深、环环相扣的“问题串”，从而将学生的思维逐步推向深入。

比如，在讲到“梯形的面积”时，教师设计问题：①你如何将梯形转化成我们已经学过的图形？②转化后的图形和原来的梯形有着怎样的对应关系？③你怎样推导出梯形的面积公式？④梯形的面积公式为什么最后要除以2？

教师按照如何转化、转化后如何、怎样推导出梯形面积公式的思维逻辑提出问题，问题的设计既有逻辑性，又有启发性，从而让学生的思维经历缓慢爬坡的过程。

（二）并列式“问题类”，拓宽思维广度

思维与问题密切相关，问题的结构化引领着思维的条理性，为学生呈现出并列式“问题类”，有利于拓宽学生的思维广度，使学生思考得更加全面、更加清晰。

比如，在讲到“圆柱的体积”时，教师设计问题：①你能用一个公式表示长方体和正方体的体积公式吗？②你认为圆柱的体积与什么有关？③猜想圆柱的体积公式，并说出你的依据。学生用“底面积×高”来表示长方体和正方体的体积公式。在此基础上，学生分析圆柱的体积可能与底面积和高有关，因为当圆柱的高一定时，底面积越大，圆柱所占的空间越大，也就是体积越大;当圆柱的底面积一定时，圆柱的高越大，圆柱所占的空间越大，也就是体积越大。至此，推测出圆柱的体积公式可能也是“底面积×高”。

并列式“问题类”引导学生的思维由长方体、正方体的体积迁移到圆柱体的体积，从而拓宽了学生的思维广度，使学生将体积的相关知识形成一个紧密联系的整体，由此完善了学生的认知结构。

三、设计衍生性问题，拓展思维

数学学习的重要目的是服务于现实生活。学生创造性地运用所学知识解决实际问题，能够拓展学生思维，开阔学生思维视野，促进学生对数学知识的再认识和再理解。

（一）学以致用，开阔思维视野

教师从学生的生活经验出发，设计现实性问题，能够引导学生从生活和应用的视角对数学知识做出不同的思考和表达，从而开阔学生的思维视野。

比如，在讲到“圆的面积”时，教师设计了如下的教学环节。

师（出示饮料瓶盖）：谁能求出这个瓶盖的面积？

生1：瓶盖是一个圆形，求圆的面积需要知道圆的半径或者直径。

生2：这个瓶盖看不见圆心，不能测量半径。

师：既然不能测量半径，测量直径可以吗？

（学生尝试测量。）

生1：我是这样测量瓶盖的直径的，把直尺放在瓶盖的弧线上，用直尺慢慢地将瓶盖“扫一遍”，当瓶盖的两端距离达到最大时，就是瓶盖的直径了。

师：同学们还有别的方法吗？

生2：我还可以用缠绕法或者滚动法测量出圆的周长，通过圆的周长计算出圆的半径，然后再求圆的面积。

……

教学中，教师引领学生提出并解决生活中的现实问题，不但提高了学生解决问题的能力，而且让学生对数学的学习从理解层面拓展到实践层面，由此开阔了学生的思维视野。

（二）转换视角，打破思维定式

针对学生的思维定式，教师设计破式性问题，能够引导学生转化思维角度，独辟思维捷径，从而帮助学生创造性地解决问题，实现思维的延伸和拓展。

比如，教师为学生出示了这样一道题目：一条绳子长度为36米，第一次剪掉了10米，第二次剪掉了9米，这根绳子比原来短了多少米？在解题过程中，有不少学生受到“见多就加，见少就减”的思维定式的影响，列出式子36-10-9=17（米），结果导致解答错误。为了打破学生的思维定式，教师拿出一捆小棒，从中取出2根，然后问道：“小棒比原来少了几根？”“2根！”学生异口同声地答道。“如果我再拿出2根，小棒比原来少了几根？”“4根！”教师继续追问：“怎样列算式呢？”学生回答：2+2=4（根）。至此，学生恍然大悟，这道题实际上在问“一共剪掉了多少米”与“这根绳子原来的长度”没有关系。

教学中，受到思维定式的影响，教师通过直观地摆小棒的方法引导学生打破思维定式，培养了学生思维的发散性和灵活性。

问题是数学思维远航的起点和动力。教师应基于学情和教学内容，精心设计数学问题，促使学生积极思考，主动探究。唯有如此，才能让学生的数学思维走向理性，走向深刻。

参考文献：

[1]  钱春梅. 数学课堂有效提问的策略[J]. 小学教学研究，2021（3）：49-50.

[2]  蒋敏杰. 小学数学课堂教学的问题设计与实施[J]. 教学与管理，2021（2）：34-37.

基金项目：教育部福建师范大学基础教育课程研究中心2021年开放课题“小学数学问题教学的实践探索”，课题编号：KCX2021050。

作者简介：何品珠（1983—），本科学历，一级教师，从事小学数学教学与研究工作。