新课程标准下初中数学课堂有效提问的策略研究
作者: 覃静
[摘 要]为落实人才培养“五育”目标,提升学生的数学核心素养,调动学生的学习积极性,切实提高学生的课堂积极参与度和思维能力,文章总结了抓住学生的兴趣点、根据学生的知识梯度、抓住课堂重难点、从学生的知识模糊点和学生的生活体验出发进行有效提问的策略。
[关键词]新课程标准;课堂提问;初中数学
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2025)06-0049-04
《义务教育数学课程标准(2022年版)》(以下简称新课程标准)提出了“三会”核心素养,即会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界。数学核心素养从哪里来?从我们的日常教学中来。“五育”融合理念下,课堂教学应该怎样提高学生的数学核心素养?笔者认为,可以通过课堂有效提问来提升学生的数学核心素养。
为了调动学生的学习积极性,切实提高学生的课堂积极参与度和思维能力,培养学生的数学核心素养,笔者总结出以下五点初中数学课堂有效提问的策略。
一、抓住学生的兴趣点进行提问
首先,教师在描述问题的时候,语言要尽量富有吸引力,努力创造出激发学生求知欲望的情境,激起学生的好奇心,让学生迫切想知道问题的答案。其次,教师提出的问题要基于学生已学过的知识,既要有一定的思考价值,又不能太难。最后,教师提出的问题应该使学生愿意跟着教师提问的思路一步步有目的地探索新知,从而提高他们分析问题、获取数学知识的能力。
案例展示:随机事件。
【师】本节课接近尾声,老师给大家讲个故事——《生死签的故事》。
相传古代有个国王,他非常阴险且多疑。一个正直的大臣得罪了这个国王,被判死刑。这个国家有一条法律:凡是死囚,在临死前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到“死”签,则立即处死;若抽到“生”签,则当场赦免。
【师】在法律中,大臣抽到“生”签是什么事件?
【生】随机事件。
【师】国王非常讨厌这个大臣,一心想置他于死地。你认为国王会想到什么计策?
【生】把两个签上都写上“死”,大臣无论抽到哪一个都必死无疑。
【师】非常正确,国王也是这么想的。他暗中让执行官在“生死签”上都写上“死”。
【师】在国王的计谋中,大臣能够获得赦免是什么事件?
【生】不可能事件。
【师】可是这个大臣非常聪明,他想到了一个妙计,最后让自己活了下来。你知道大臣想到了什么妙计吗?
【生】不知道。
【师】这个大臣抽了签后立即吞下所抽的签,他表示,自己吞下的是什么签就接受什么样的结果。因为他知道剩下的签肯定为“死”签,他这么做是想让朝廷中的所有人都认为他吞下的是“生”签。结果国王怕失去威信,只好当众释放了这个大臣,大臣重获新生。
【师】在大臣的计谋中,他能够获得赦免是什么事件?
【生】必然事件。
【师】通过这个故事,你悟出了一个什么道理?
【生】三类事件在一定条件下可以相互转化。
【师】没错,在生活中,很多看似不可能完成的事情,只要我们肯动脑筋,“不可能”也会变成“可能”或者“必然”。
二、根据学生的知识梯度进行提问
教学是一个循序渐进的过程,学生的学习同样也是一个循序渐进的过程。教师在设计课堂提问时要结合学生的认知规律,提出的问题应该由易到难、由浅入深,体现一定的知识梯度和有序性,引导学生探讨思考问题的方向,培养学生分析问题、解决问题的能力。
案例展示:过不在同一直线的三个点能否作圆?
课件展示问题:确定一个圆需要多少个点?是一个?两个?还是三个?
展示问题1:平面上有一个点[A],经过已知点[A]的圆(即点[A]在该圆上)有几个?
【师】请同学们拿出草稿纸和圆规,在草稿纸上随意取一个点[A],画一个圆,使得点[A]在圆上,这样的圆可以画几个?
【生】可以画无数个。
【师】课件展示:这样的圆圆心在哪里?
【生】只要不在点[A]就可以。
【师】很好。
适时小结:过一个点可以作无数个圆,圆心为点[A]以外的任意一点。
展示问题2:平面上有两个点[A]、[B],经过已知点[A]、[B]的圆(即点[A]、[B]在该圆上)有几个?
【师】请同学们在草稿纸上再随意取两个点[A]、[B],你能作出一个圆,使得点[A]、[B]都在该圆上吗?圆心可以取在哪里?
【生】连接[AB],以[AB]的中点为圆心能作出一个圆。
【师】很好,除了[AB]的中点,还有其他位置的点可以作为圆心吗?
【生】有的学生说没有,有的学生说有。
【师】要想使得[A]、[B]两个点都在圆上,圆心[O]应该满足什么条件?
【生】[OA=OB]。
【师】非常好,点[O]应该在哪里才能满足[OA=OB]的呢?
【生】点[O]应该在线段[AB]的垂直平分线上。
【师】所以这样的圆能作几个?半径如何确定?
【生】可以作无数个圆,半径为[OA]或[OB]。
适时小结:过任意两个点可以作无数个圆,它们的圆心都在线段[AB]的垂直平分线上。
展示问题3:平面内有三个点[A]、[B]、[C],经过这三点的圆(即点[A]、[B]、[C]在该圆上)有几个?
【师】请同学们在草稿纸上再随意取三个点[A]、[B]、[C],你能作出一个圆,使得[A]、[B]、[C]三点都在该圆上吗?
【生】先随意画出三个点,然后无从下手。
【师】同学们取的三个点的位置关系可以分为几种呢?
【生】三个点在同一条直线上,或者三个点不在同一条直线上。
【师】那我们先来探究三个点不在同一条直线上的情况。要使[A]、[B]、[C]三个点都在圆上,圆心[O]应该满足什么条件?
【生】[OA=OB=OC]。
【师】要使得点[O]满足[OA=OB],则点[O]应该在哪里?
【生】点[O]应该在线段[AB]的垂直平分线上。
【师】要使得点[O]满足[OB=OC],则点[O]应该在哪里?
【生】点[O]应该在线段[BC]的垂直平分线上。
【师】既然点[O]要同时满足分别在线段[AB]、[BC]的垂直平分线上,这样的点[O]如何确定?
【生】分别作出线段[AB]、[BC]的垂直平分线,取它们的交点,这个点就是点[O]。
【师】非常好!请同学们用尺规作图法在你的草稿纸上作出这个圆。
【生】按要求作图。
适时小结:不在同一条直线上的三个点确定一个圆。
三、抓住课堂重难点进行提问
教师的提问应该紧紧抓住课堂重难点,提问要精而准,问题要经得起推敲,问题与问题之间要有联系、有层次,力争让每个问题都形成一个有机的整体,让学生通过解答这些问题既能理解和掌握知识,又能提升自身的逻辑思维能力。
案例展示:切线的判定定理。
【师】上节课我们学习了直线和圆有哪几种位置关系呢?
【生】相交、相切、相离。
【师】这三种位置关系中,最特殊的关系就是相切。那么如何判断直线和圆相切呢?上节课我们总结了几种方法?
【生】两种。
【师】哪两种?
【生】学生回答。
【师】教师在课件上展示这两种方法。
方法一,用交点个数来判断:直线与圆相切,直线与圆只有一个交点。
方法二,用圆心到直线的距离[d]与半径[r]的关系来判断:直线l与⊙O相切, [d=r]。
【师】这节课,我们继续来探究判定直线和圆相切的第三种方法。现在请同学们拿出草稿纸和圆规,在草稿纸上随意画一个[⊙O],画好了吗?
【生】按教师要求作图。
【师】请你在[⊙O]上任取一个点[A],经过半径[OA]的外端点[A]作直线[l⊥OA]。
【生】按教师要求作图。
【师】请问,圆心[O]到直线l的距离是多少?
【生】[OA]。
【师】很好,那么直线l和[⊙O]有什么位置关系?
【生】相切。
【师】你是怎么判断它们相切的?
【生】圆心到直线l的距离[OA]等于半径的长度,即[d=r]。
【师】非常好,刚才我们在画图的过程中,直线l是经过了半径外端,并且垂直于半径[OA]的,由此我们可以得出判定直线和圆相切的第三个方法:用切线的判定定理,即经过半径的外端且垂直于这条半径的直线是圆的切线(课件展示)。
四、从学生的知识模糊点进行提问
知识的模糊点指学生对一个问题懂了一部分,但是还存在疑惑。教师需要在教学中进行积极的课堂反馈,根据学生的知识模糊点有针对性地设计课堂提问,使学生更全面、透彻地理解教学内容,提高学生分析问题的能力。
案例展示:圆周角定义。
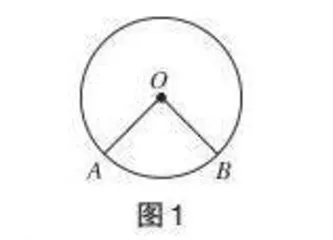
【师】展示课题“圆周角”,并展示圆心角(见图1)。上节课我们学习了圆心角的定义,大家还记得我们是如何给圆心角下定义的吗?
<H:\中学教学参考\中学教学参考2025年第2月(综合科下旬)\36.tif>
图1
【生】顶点在圆心上的角称为圆心角。
【师】很好。其实在圆内,还有一类角,如图2中的[∠ACB],这就是我们今天要学习的圆周角。你能仿照圆心角的定义给[∠ACB]这类角下个定义吗?
<H:\中学教学参考\中学教学参考2025年第2月(综合科下旬)\37.tif>
图2
【生】顶点在圆上的角称为圆周角。
【师】展示图3、图4,根据刚才同学们给圆周角下的定义,请同学们判断:图3、图4中的[∠ACB]是圆周角吗?
<H:\中学教学参考\中学教学参考2025年第2月(综合科下旬)\38.tif><H:\中学教学参考\中学教学参考2025年第2月(综合科下旬)\39.tif>
图3 图4
【生】不是。
【师】为什么不是呢?图3、图4中的[∠ACB]都满足顶点在圆上的条件了啊?
【生】这两个角都不在圆内。
【师】哪位同学能完善一下圆周角的定义?
【生】学生在教师的引导下得出圆周角的定义:顶点在圆上,并且两边都和圆相交的角叫作圆周角。