三视图补线技巧——线面法、数点法

［摘 要］三视图补线是通用技术高考中的一种经典题型，因其对学生综合素养的高要求而成为教学的重难点。文章根据三视图形成过程（正投影）的特征提出两种补线技巧：线面法和数点法。线面法，即将体的投影视为多个面的投影之和，根据某面正投影的真实性、相似性、积聚性特征补线并验证；数点法，即在线面法的基础上，将某个面的投影视为多个点的投影之和，根据某点正投影的三等关系特征以及数点的顺序补线。将体的投影逐步分解为面、线、点的投影便可大大降低思维难度，提高解题速度与正确率。

［关键词］三视图；正投影；线面法；数点法；相似性

［中图分类号］    G633.98            ［文献标识码］    A          ［文章编号］    1674-6058（2024）27-0018-03

《普通高中通用技术课程标准（2017年版2020年修订）》对“图样表达”核心素养的说明为：学生能识读简单的机械加工图及控制框图等常见技术图样；能分析技术对象的图样特征，会用手工和二维、三维设计软件绘制简单的技术图样等；能通过图样表达设计构想，用技术语言实现有形与无形、抽象与具体的思维转换。

三视图作为培养学生图样表达能力的一个载体，以补线的形式出现，旨在让学生根据已有的线条分析物体的结构特征。通过省去轴测图的方法，让学生想象该结构的加工或绘制过程，以更好地检测学生抽象思维与具体思维的转换能力。三视图补线因空间想象难度大，对学生综合素养要求高，而成为通用技术考试中的重难点。如何在短时间内准确地完成补线，是提高分数、拉开差距的关键。为此，教师总结出了许多解题技巧，如轴测图绘制法、拐点法等。笔者所在的教研组通过探究三视图形成过程（正投影）的特征，尝试提出线面法、数点法这两种补线技巧，希望能为相关的教育教学提供参考。

一、思路简介

将某个结构体的投影分解为构成该结构的面的投影，甚至分解到点，逐步降低空间维度，从而降低思维难度，是本文中两种三视图解题技巧的关键思路。因此，从分析面与点的投影特性出发，可以帮助我们更好地理解并掌握解题技巧。

物体在光线的照射下，会在地面或墙面上投下影子。正投影即当投射线与投影平面垂直时，在投影平面上求取物体的投影方法。本节将简单阐述在正投影下面和点的投影特征，以及依据这些特征而提出的线面法和数点法。

（一）面的正投影特征及线面法

1.面的正投影特征

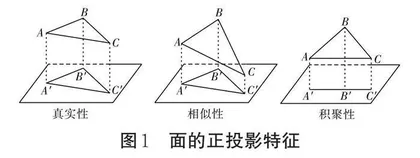
由正投影易得：当面ABC与某一投影面平行时，所得的投影即为其本身；当面ABC与某一投影面处于倾斜状态（成一定的角度）时，所得的投影则是一个与其本身形状一致但面积有所缩小的图形；当面ABC与某一投影面垂直时，所得的投影将积聚为一条线段。我们可以将这三种不同情况下的投影特征分别称为真实性、相似性、积聚性，如图1所示。

2.线面法

对于一个复杂的物体，为了更加准确地描述其结构形状，我们一般会采用多面正投影法——利用三个互相垂直相交的投影面（正面投影面V、水平投影面H和侧面投影面W）建立一个三投影面体系，再采用正投影法将物体同时向三个投影面投影，得到三个投影图，分别称为主视图（由前向后，在正面投影面上形成的投影图）、俯视图（由上向下，在水平投影面上形成的投影图）和左视图（由左向右，在侧面投影面上形成的投影图）。主视图、俯视图、左视图统称为三视图，如图2所示。

若某个面（如面ABCD）的位置非常特殊，与三个投影面中的两个投影面V、W都垂直，与另一个投影面H平行。根据面的正投影特征可知，该面在投影面V和投影面W上的投影均为一条水平的线段——积聚性；在投影面H上的投影与其本身的形状大小均一致——真实性。它的三个投影图可简称为“两平线一面”，如图3（a）所示。

若某个面的位置较为特殊，仅与一个投影面V垂直，与另两个投影面W、H均呈倾斜关系。根据面的正投影特征可知，该面在投影面V上的投影为一条倾斜的线段——积聚性；在投影面W、H上的投影均为一个与其本身的形状一致但面积有所缩小的图形——相似性。它的三个投影图可简称为“一斜线两面”，如图3（b）所示。

若某个面的位置关系一般，与三个投影面V、W、H均呈倾斜关系。根据面的正投影特征可知，该面在投影面V、W、H上的投影均为一个与其本身形状一致但面积有所缩小的图形——相似性。它的三个投影图可简称为“三面”，如图3（c）所示。

线面法口诀为“两平线一面”“一斜线两面”“三面”。我们可以从三视图已给出的轮廓线的“平”“斜”“虚”“实”来判断被投影面与投影面的位置关系，再根据口诀补全缺失的图线并利用投影的相似性判断所补线条的正确性。

（二）点的正投影特征及数点法

1.点的正投影特征

在三视图中，主视图反映物体的长和高，俯视图反映物体的长和宽，左视图反映物体的高和宽。因此三视图存在以下投影规律：主、俯视图长对正；主、左视图高平齐；俯、左视图宽相等——三等关系。

2.数点法

若某个面的形状复杂或位置关系一般（与三个投影面均呈倾斜关系），其在某视图中投影图线缺失时，需要补线。由于题中未提供轴测图，单凭空间想象难度较大且易出错。此时可再次进行降维处理——将面的投影看作点的投影的连线。

如图5所示，已知某面与三个投影面均呈倾斜关系，其在主视图、左视图中的投影是完整的，现在需要在俯视图中画出该面的投影。

我们可以在主视图中将该面上的点按照一定的顺序标号，再根据高平齐原则标出这些点在左视图上的位置，接着根据长对正、宽相等原则找出各点在俯视图的投影并按照顺序连线，最后还可用所得投影的相似性检验所补线段的正误。

二、补线技巧及其应用

当我们面对一个结构体时，首先可用组合或切割的思路粗略分析其大致的加工过程；再根据加工的过程，将体的投影看成是由加工所得的面的投影的总和；最后借助线面法、数点法等技巧进行解题。

（一）例题

请补全三视图（如图6）中所缺的3条图线。

该结构可看作由一个长方体进行三步加工而得。第一步，由主视图可得，该长方体的左上角切去了一块截面为梯形的四棱柱；第二步，由俯视图可得，该长方体的左前方切去了一块截面为三角形的三棱柱；第三步，结合三视图可得，该长方体的右后方切去了一块复杂结构，切割后形成了一个与三投影面均不垂直的面。（立体图仅为帮助理解，实际解题时无须绘制。图7中的1、2、3分别对应三步加工形成的部分加工面）

（二）线面法及其应用

观察例题，我们发现加工面1与正面投影面和侧面投影面均垂直，与水平投影面平行，因此它的投影属于“两平线一面”的类型。结合已有三视图很容易发现主视图左侧加粗的水平线段和左视图对应等高位置处加粗的水平线段为该加工面的“两平线”；可推断在俯视图的对应处缺少“一面”，如此便可快速锁定位置并根据三等关系补线，如图8（a）所示。

再观察俯视方向切去三棱柱后形成的加工面2，该面与水平投影面垂直，与正面投影面和侧面投影面均倾斜，其对应的投影应属于“一斜线两面”的类型。俯视图左下角的一条加粗倾斜线段即为“一斜线”，主视图中与该斜线长对正之处已有一五边形，根据高平齐和宽相等原则可在左视图对应位置处补出另一个形状相似的五边形，这两个五边形即为“两面”，如图8（b）所示。

此题的易错点在于不少学生会从左视图的拐点（黑点标注处）作垂线，如此所得的图形为四边形。在掌握了线面法后，学生可由相似性规律（两投影形状一致，应均呈现为五边形）自行检查，以判断所补线段的正误。

（三）数点法及其应用

当某个面与任一投影面均不垂直时，三个投影面上会呈现出三个相似的面，即“三面”。这类投影涉及的维度更多，立体感更强，需要降维处理，此时可使用数点法。

此题的难点为右后方切去一个复杂结构后所形成的加工面3，该加工面与三个投影面均呈倾斜关系，其对应的投影应属于“三面”的类型。观察可得，该结构在主视图与左视图上的投影是完整的，且均为四边形，可推断在俯视图对应处需补出一个形状相似的四边形。

如图9所示，应用数点法补线：先按照顺时针的顺序将主视图四边形的各个点标为ABCD，再根据高平齐原则在左视图上标出各点的对应投影[A'B'C'D']（由于BC等高，光凭高度关系难以直接确定具体的位置，此时可根据连接的顺序判断出与[A']相连的是[B']）。确定了四个点在主视图、左视图上的位置后，使用三等原则画出各点在俯视图上的对应位置，再将所得的点按照顺序连线并根据相似性规律判断正误。（图9中仅展示了点A投影的寻找过程）

三、现有方法优缺点总结

三视图补线是通用技术高考中的常考题型，以往补线时常用的方法主要有：轴测图绘制法、拐点法。轴测图绘制法：根据已有的三视图，用组合法或切割法逐步绘制出轴测图。该方法能够很好地展现结构加工成形的整个过程，并引导学生立足整体去解题。所绘的轴测图虽然可以降低对空间想象能力的要求，但该方法所花费的时间较长，且对学生绘制图样的能力有较高的要求。拐点法：常用的口诀是“有折必有线”。该方法虽然可以帮助我们快速锁定因面面相交而产生的交线，但只能大致判断交线所在的位置，无法确定线段的起始点。当物体结构复杂时，有转折的地方也可能只呈现为一个折点而非交线。在这种情况下若依旧使用拐点法，会将解题者的思路引入歧途。

本文介绍的线面法和数点法立足整体、着眼局部，是根据正投影的原理，依照“体—面—线—点”的投影层层降维的分析方法，在复杂结构中有较好的应用。但这两种方法对学生的基础有一定的要求，初学者在理解和应用上会有些困难。

三视图在通用技术纸笔测试中有着举足轻重的地位，“图样表达”核心素养是高校理工科类专业需具备的重要素养，其包含的抽象思维与具象思维相互转换的能力在生活的各个方面都有或大或小的作用。技巧可以帮助我们高效解题，但想真正实现质的飞跃仍需将精力放在空间想象能力的提升上。以培养能力为主、善用技巧为辅，能够根据不同题型的特点灵活选择适合的补线技巧是三视图提分的关键。

［   参   考   文   献   ］

［1］  中华人民共和国教育部.普通高中通用技术课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020.

［2］  梁灵辉，陈湛.指向深度学习的三视图变式设计［J］.中学教学参考，2021（30）：42-44.

［3］  朱仕成.基于平面立体的三视图绘制正等轴测图教学探析［J］.中学理科园地，2021（1）：60-61.

［4］  沈杰.三视图补线线索探究［J］.新课程（下），2019（11）：222-223.

［5］  顾建军.高中通用技术教学参考书    必修    技术与设计１［M］.南京：江苏凤凰教育出版社，2009.

（责任编辑 罗 艳）