核心素养背景下“发现与提出问题”驱动教学的探索

［ 关键词 ］ 核心素养；发现问题；提出问题；复习教学

《义务教育数学课程标准（2022年版）》（简称“新课标”） 依然将发展学生的数学核心素养作为教学的核心目标.其中，发展学生的“四基与四能”是必不可少的环节，“四能”是指发现问题、提出问题、分析问题与解决问题的能力.但一些教师只关注对学生“分析与解决问题能力”的培养，而忽略了“发现与提出问题”的重要性.为此，笔者做了大量实践与探索，现以初中复习教学为例，展开分析与思考.

培养发现与提出问题的能力是提高复习成效的基本策略

1. 自主提问，建构结构化的知识体系

从认知心理学的角度出发，学生能否将所学知识举一反三地应用在实践中，关键取决于能否将所学知识结构化与体系化.新知的学习一般为点状、碎片式，即使基于整体单元视域进行教学，但由于学生在获取知识的过程中，后续还有很多内容没有接触到，所以难以形成完整的知识结构，且在实际应用时，常因认知的不足而束手束脚.复习教学是在章节或单元教学已经结束的基础上进行的，此时可引导学生将点状的知识以一定的逻辑主线串联起来，形成结构清晰的知识体系.

纵然教师有结构化教学的意识，但复习时，仍有部分教师只要求学生回顾知识点的概念、性质、定理等，因为缺乏从宏观的角度对知识进行统摄的思想，所以学生的思维含量不够，难以形成完整的知识结构；也有部分教师直接将自己准备好的思维导图或知识结构图展示给学生，导致学生缺乏思考的过程，应用时无法触类旁通.基于“四能”发展的复习教学，应关注学生自主发现并提出问题的过程，想方设法地提高学生建构知识的主动性.

案例1 “二次函数”的复习教学

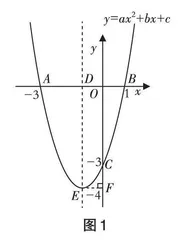
师：大家已经了解了二次函数的相关内容，现在请观察图1.若让你根据图象提一个问题，你会提出什么问题呢？

常规情况下，复习课都是教师提问，学生思考，此处教师要求学生自主提问，学生都来了兴致. 兴趣使然， 学生提出的问题异常丰富：①请写出该抛物线的解析式；②该抛物线的对称轴是什么？③请说说抛物线与坐标轴的交点坐标．④说说该抛物线的顶点坐标．⑤该抛物线是否存在最值？是多少？⑥分析该抛物线在什么情况下，y 会随x 的增大而增大（减小）．⑦写出点C 关于直线DE 的对称点坐标……

师：这些问题分别是从什么角度提出来的？若换个角度，提出的问题还一样吗？

在教师的提醒下，学生发现这些问题都是从二次函数图象的特征与性质的角度所提.思索片刻，有学生提出如下问题：①分析一元二次方程ax²+bx+c=0是否存在根，若有，是多少？②怎样根据二次函数的解析式与图象，明确与之相对应的一元二次方程根的情况？

随着这两个问题的落地，有学生发出赞叹，原来还可以从这个角度来提问.在这两个问题的启发下，

学生又如雨后春笋般地提出很多问题：分析ax²+bx+c=-3的根；若将图中的抛物线先向下平移2 个单位长度，再向右平移3 个单位长度，写出此时抛物线的解析式；若将抛物线绕点E 进行旋转，求转了180°时抛物线的解析式；若将该抛物线在x轴以下的部分向上翻折，写出新的图象的解析式；点A，B，E，F 在同一个圆上吗……

随着更多问题的呈现，教师鼓励学生结合这些问题对知识进行分类，勾勒出关于二次函数的结构图.

学生自主画图，教师投影典型图示（见图2） .

分析 以上教学过程，教师以一个开放性的情境鼓励学生自主提问，并在适当时机进行点拨，成功引导学生自主画出了二次函数的知识结构图，帮助学生构建了完整的知识体系.在此过程中，学生的思维被不按常理出牌的教师所激活.在兴趣的基础上进行学习，效果自然事半功倍.随着一个个问题的提出，二次函数的内外部结构也逐渐清晰，知识间的联系也越发明朗.在教师适当启发下，学生自主分类、类比，不仅成功设计出了完整的知识结构图谱，还进一步提升了自主发现问题与提出问题的能力，为“四基”的发展夯实了基础.

2. 变式拓展，多维度理解与分析问题

专题复习一般以解决问题为目的，这是提升学生解题能力的根本.但当前一些教师将问题解决与解题教学、题型教学等混为一谈，认为通过“刺激—反应”训练就能让学生形成良好的解题能力.显然，这是一种窄化问题解决能力的理解.其实真正的问题解决能力不仅涵盖了分析与解题的环节，还包括发现与提出问题的环节.

核心素养背景下，如何以发现与提出问题的方式来推动解决问题能力的发展呢？教师可引导学生发现给定情境中的问题，也可以鼓励学生通过对已知问题的修改产生新的问题.在专题复习过程中，学生首先接触到的是原始问题，教师可引导学生基于原始问题进行变式与延伸，由此提出系列问题，发展学生的思维能力.这种方法是当前课堂常用的一种方法， 但对发展学生的“三会”能力没有太大作用.

新课标强调要引导学生学会用数学的眼光、思维、语言来观察、思考、表达现实世界（简称“三会”能力） .因此，教师在专题复习时，应更多地从这个角度去思考，这对发展学生的解题能力与创新意识具有重要意义.

案例2 几何专题复习——探究变化中的不变

问题 如图3，已知△ABC 为一个等边三角形，点D 为该三角形BC 边上的一点，若以AD 为边作一个等边三角形AED，其中DE 与AC于点F 处相交. 请证明：点E 位于△ABC 的外角平分线上.

在学生自主成功解题的基础上，教师要求他们从原题出发，提出新的问题，如推广问题的条件、改变探索结论的范围等.学生自主思考，提出如下新的问题.

问题1 若点D 为射线BC 上的一点，此时的点E 依然位于△ABC的外角平分线上吗？

问题2 设点D 位于直线BC 上，那么点E 依然位于△ABC 的外角平分线上吗？

问题3 如果将△ ABC 与△AED 均转化为正方形，此时的点E 依然位于△ABC 的外角平分线上吗？

令学生感到意外的是，这三个问题的结论竟然未发生变化.这是为什么呢？学生的探究热情逐渐高涨.为了让学生做到知其然且知其所以然，笔者点拨学生可以考虑换个角度思考问题，如将条件与结论互换等.随着教师的引导，学生瞬间就有了灵感.

问题4 在其他条件不变的情况下，将“点E 位于△ABC 的外角平分线上”作为问题的条件，思考△AED 是否一定是等边三角形.

学生自主思考与合作交流，并提出可以添加条件，如增加角度为60°或边相等的条件，可让△AED一定为等边三角形.

分析 该教学片段，学生在教师的启发与点拨下，分别从不同的视角发现并提出了一些高质量的问题.这是深化学生对运动变化过程中不变性的理解过程，是发展数学分类讨论思想的过程，亦是培养思维深刻性、灵敏性与发散性的过程.因此，这种教学方式对发展学生的核心素养具有深远的意义.此外，随着问题的逐渐深化，学生对问题的探索欲越来越浓厚，学生通过自主提问不断深化对问题间的区别与联系的认识，这是发展“四能”的根本.鉴于此，将这种方式应用在专题复习课堂，不仅能有效改善课堂的生态环境， 还能促进教育的高质量发展.

问题驱动复习课的建议与思考

1. 情境是盛产问题的营养基

新课标认为情境是问题的“出产地”，数学教学应结合学科素养要求与教学特点设计贴合学生生活实际的情境，以促使学生学会用数学的眼光来观察这个世界，并从中自主发现并提出问题，这是发展“四能”的基础.复习教学之前，学生虽然已经掌握了相应的知识点，但这种掌握比较零碎，想要形成结构化的知识体系，还需结合教学目标与学生的认知水平来构建有意义的情境，引导学生透过情境来主动发现并提出问题.

本文呈现的两个教学片段，教师分别以“ 二次函数的图象” 与“具体的问题”为情境，这两个情境都是学生熟悉的内容，其中蕴含着丰富的知识点与数学思想. 教师以这两个开放性情境作为教学的出发点，成功激活了学生的思维，催生了学生的问题意识，让学生不由自主地进入问题的探索中. 实践证明，复习课型中的情境，既可以是某个具体的数学问题，也可以是典型的错误解法，抑或是与学生生活相契合的一种场景. 不论是以哪种方式呈现的情境，都要避免机械、空洞等问题.

2. 提出的问题需讲究逻辑性

想要在发现与提出问题的基础上推进复习课的进展，关键要避免如下两类情况：①放任学生随意地问.这种毫无逻辑的乱问与瞎问只会让课堂成为一团乱麻，最终毫无进展可言.教师需在课堂上引导学生遵循一定的逻辑顺序来发现并提出问题.②学生大脑一片空白，无法自主发现并提出问题时，教师直接抛出问题.事实证明，高质量的问题要以一定的观念、思想与思维指导作为基础，教师站到整体的角度进行适当点拨，可激活学生的思维，促使学生提出一些具有探究价值的好问题.

因此，当学生无法提出令人满意的问题时，教师可引导学生转变视角，通过对数学思想、观念、思维策略等的点拨，启发学生提出恰当的问题，切忌直接给出问题草草结束学生的思考.

3. 兼顾发现、提出、分析与解决问题的教学

复习课教学，虽然以学生的解题为主要评价指标，但并不是会解题就从真正意义上促进了“四能”的发展. 只有兼顾“发现与提出问题”与“分析与解决问题”的平衡，才能真正地促进学生核心素养的发展.

因此，教师可从学生所提的问题中择取一些具有代表意义的高质量问题作为解题教学的起点.如案例1 中学生刚开始提出的问题并不复杂，教师可以带领学生边说问题边说解题思路；案例2 中的问题相对复杂了一些，则需单独提取典型问题与学生一起分析，让学生的思维经历完整的发现问题、提出问题、分析问题与解决问题的过程，这是完善认知结构的基础.

总之，课堂以培养学生的思维为目标， 发展学生的“ 四能” 与“三会”能力是新课标对我们提出的要求.复习课型作为完善知识体系、搭建知识框架的重要课型，值得每一位教师去实践与探索，这是落实新课标要求、发展核心素养的关键.