搭建思维阶梯 提升复习质量

[摘  要] 复习课是数学教学的重要课型，是建构知识体系、提高解题能力、发展学生思维能力的必经之路. 复习教学中，若纯粹地进行知识重现和没有针对性、梯度性的重复练习，不仅会增加复习课的枯燥感，而且会影响学生的学习信心. 教师应以学生已有知识经验为出发点，结合实际问题创设梯度问题，以帮助学生扫除障碍，体验成功，认清本源，实现知识的融会贯通.

[关键词] 复习课;梯度问题;融会贯通

复习是回顾旧知识，形成知识网络和系统架构的一个非常关键的环节，尤其是在中考前开展的综合复习课程，更是帮助学生梳理以往所学知识的重要方式. 复习不是简单地将知识重现，而是在巩固原有知识的基础上，对所学知识进行归类、整合、深化，将所学知识串成串、连成网，构建知识体系，从而实现知识的融会贯通. 在初中数学复习教学中，教师应从学生现有知识水平入手，层层深入，帮助学生认清问题的本质，掌握解决问题的通法，充分调动学生参与课堂的积极性，引导学生亲历观察、操作、交流、思考等过程，让每个学生都能有所收获，切实提升复习课的效率.

提出问题

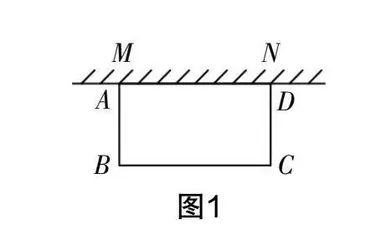
例1  如图1，王大伯想用木栏靠墙MN围一个矩形ABCD菜地，其中墙的长度为a米，木栏总长为100米.

（1）已知a=20，王大伯利用100米的木栏围成了一个面积为450平方米的矩形菜地，试问围成这样的矩形菜地，需要利用的墙长是多少？

（2）如图2，已知0<a<50，若王大伯想用这些材料围成一个最大面积的菜地，你认为可以怎么围？面积最大值是多少？

例1是一道典型的二次函数应用题，初看上去毫无探究性，但是认真分析不难发现，第（2）问中巧妙地对墙的长度做了模糊处理，使得看似陈旧的老题变得更加有新意，大大地提升了题目的整体难度. 从解题反馈上来看，几乎所有的学生都能顺利地完成第（1）问，但是在完成第（2）问时，很多学生露出了愁容，感觉无从下手. 面对这一现象，若教师直接给出答案，学生也能够理解，但由于没有经历自主探究的过程，学生便不能认清问题的本质. 日后遇到此类问题时学生依然会茫然，从而影响自身解题能力和解题信心的提升. 基于此，在复习教学中，教师应从学生认知规律出发，循序渐进，逐渐帮助学生厘清问题的来龙去脉，揭示问题本质，提升复习质量.

教学过程

1. 剥茧抽丝，循序渐进

教学中，为了帮助学生突破问题（2）这一难点，教师为学生设计了层层递进的问题，以此为学生的思维搭建梯子，充分调动学生思考的积极性.

问题1：用一个长为100米的木栏围一个矩形菜园，若使矩形面积最大，可以怎么围？最大面积是多少？

学生活动：问题给出后，学生独立完成. 解题过程如下：设矩形的一边长为x米，则矩形的另一边长为（50-x）米，于是矩形的面积为S=x（50-x）=-（x-25）2+625，所以当x=25时，矩形的面积最大，最大值为625平方米.

问题2：若矩形的周长不变，怎么围面积最大？给出你的理由.

师生活动：学生独立探索，对于基础较弱的学生，教师适时给予指导. 学生给出如下解题过程：设木栏的长度为m米，矩形的一边长为x米，则矩形的另一边长为

-x米，则S=x

-x=-x-

2+. 由此可知，当矩形的周长一定时，所围成的矩形是正方形时，面积最大.

设计意图  从学生熟悉的题目入手，通过由特殊到一般的探究，引导学生归纳总结解决此类问题的方法，提炼蕴含其中的规律，从而为后续的探究做好铺垫，提高学生分析和解决问题的能力.

问题3：回归例1，若a=60，AD的长是多少米时，所围的矩形ABCD的面积最大？

学生活动：有了前面的铺垫，学生解题时显得轻松自若. 设AD=x米，则AB=米，所以S=x·= -（x-50）2+1250，即当矩形的长为50米时，矩形的面积取最大值1250平方米. 这里50<60，符合题意.

问题4：若a=40，AD的长是多少米时，所围的矩形ABCD的面积最大？

师生活动：结合以上经验，得出S=x·=-（x-50）2+1250. 根据二次函数的增减性可知，当x=40时，面积取最大值1200平方米.

问题5：若a=20，AD的长是多少米时，所围的矩形ABCD的面积最大？

师生活动：学生结合研究问题4的经验，直接给出结果，即当x=20时，面积取最大值800平方米. 学生得到这一结果后，教师提出疑问：当AD的长为20米时，真的可以使面积最大吗？在问题的引导下，学生继续探索，进而通过深度思考突破矩形的一条边只能是墙的束缚，发现墙也可以用木栏延长，此时S=x·=-（x-30）2+900，这样将墙用木栏延长10米，便可获得更大面积的矩形，此时矩形的面积为900平方米.

设计意图  通过变式训练逐渐激活学生的数学思维，此时学生已经认识到，墙也可以作为矩形一边的一部分，有效地打破了定式思维的束缚，使学生的思维向更高层级进阶. 同时，在此过程中，教师为学生创设问题台阶，让学生拾级而上，有利于增强学生的自信心，提高学生分析和解决问题的能力.

2. 高屋建瓴，融会贯通

通过以上问题的解决，学生已经逐渐认识到，墙的长度影响着矩形的围法. 在此基础上，教师乘胜追击，引导学生从三个变式中寻找规律，由此使课堂再度升华，帮助学生厘清知识脉络，提高数学思维品质.

问题6：若墙长为a米，木栏长为100米，怎么围可使矩形ABCD的面积取最大值？

师生活动：该问题具有一定探究性，是解决第（2）问的关键，教师启发学生回顾前面三个变式问题，思考当a=60，40，20时，是如何围矩形的？由此把问题聚焦于对a的取值范围的讨论. 结合以上探究过程，学生明确要解决这个问题需要分三种情况讨论：（1）当a取何值时，墙足够长;（2）当a取何值时，把整个墙作为矩形的一边;（3）当a取何值时，把墙作为矩形一边的一部分. 教学中，教师给予学生充分的时间对这三种情况进行逐一探究，然后以小组为单位合作交流，最终形成统一的结论：当a≥50时，墙足够长，此时S=1250;当≤a≤50时，墙长为矩形一边的边长，此时S=-（a-50）2+1250;当0<a<时，墙长为矩形边长的一部分，此时S=

2. 学生经历由特殊到一般的探究后，有效地升华了认知，发展了数学思维能力. 结合以上探究过程，例1中的问题（2）迎刃而解.

问题7：若a=20，木栏的长为b米，其他条件不变，怎么围可使矩形ABCD的面积最大？

由于课堂时间有限，教师让学生以小组为单位，课下共同完成问题7. 通过适度的拓展延伸，不仅可以检测学生的知识理解情况，而且可以发散学生的数学思维，培养学生数学思维的深刻性、变通性.

教学感悟

复习教学中，部分教师为了能够多讲多练，常常简单分析后就直接给出正确答案. 学生虽然能听得懂，但由于没有经历自主探究的过程，很难产生深刻的印象. 在遇到类似的题目时，学生依然会出现“懂而不会”“一错再错”等情况. 在复习教学中，教师应该控制好教学节奏，给学生一定的时间和空间进行独立思考和合作探究，引导学生经历知识生成发展的过程，从而加深知识理解，促进知识内化.

另外，复习教学应着重发展学生的逻辑思维，引导学生整体思考数学问题，使学生的思维能力得到全面发展. 在具体实施过程中，教师不能满足于单一问题的解决，应站在整体的视角引导学生思考与探究，一方面让学生将相关知识有效地串联起来，完善认知体系，另一方面让学生在对比分析中，认清问题的本质，掌握解决此类问题的方法，提高举一反三的能力. 在本课教学中，教师没有直接讲解问题，而是从学生熟悉的问题入手，让学生通过由特殊到一般的探究得到“当矩形的周长一定，所围图形为正方形时，其面积取最大值”，以此培养学生的整体观. 在此基础上，教师又合理地设计变式问题，通过梯度问题搭建思维进阶的阶梯，使学生的数学思维获得了更大程度的发展. 另外，教师不断渗透分类讨论、特殊到一般、数形结合等数学思想方法，有效打通了各个知识点的联结脉络，有利于学生认知结构的优化以及分析和解决问题能力的提升.

总之，在复习教学中，教师不能盲目地向学生灌输知识，更多的是去启发、去唤醒. 教师要以学生已有知识经验为基础，结合教学实际创设环环相扣、层层递进的问题，引导学生经历问题解决的全过程，追溯问题的本源，认清问题的本质，掌握解决问题的方法，以此提高学生的数学应用能力，提升复习教学质量.