立足课堂编题 优化复习教学

［摘  要］ 带领学生在复习课中自主编题，可进一步激活学生的思维，发展学生的应用意识与创新意识，培养学生的数学核心素养.文章以“全等三角形”的复习教学为例，立足于课堂编题活动的开展，分别从“展示教具揭露主题、编题探索判定方法、总结提炼发展能力”三个维度展开研究.通过学生自主编拟、分析与解决问题来优化数学复习教学，发展思维，培育数学核心素养.

［关键词］ 复习；编题；教学

复习教学是对已学知识或方法的梳理与巩固，对提升解题能力与数学思维具有重要意义.然而，当前的复习教学，部分教师只关注“教”的过程，对于学生“学”的过程关注度还不够，由此导致学生无法真正厘清知识之间的联系，难以构建完整的知识结构.探索发现，引导学生在复习课中自主编题，可进一步激活学生的思维，发展学生的应用意识与创新意识，培养学生的数学核心素养.

教学分析

《义务教育数学课程标准（2022年版）》中关于“全等三角形”的内容，提出的教学要求为：理解全等三角形中的对应边与对应角；掌握什么情况下两个三角形全等；会用定理证明三角形全等［1］.该阶段学生的几何素养不高，虽然学生已经在新授课中掌握了什么是全等三角形，能根据图形判断出全等关系，但对判定方法的掌握程度依然还不够.为此，复习教学时教师除了帮助学生巩固基本概念与基本性质，还要加强学生对判定方法的理解，让学生经历自主画图探索的过程，有效提升几何能力，为发展学生的数学核心素养夯实基础.

教学过程设计

1. 展示教具揭露主题

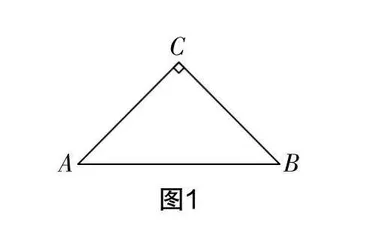
教师展示常用的教具——等腰直角三角板，要求学生用自己的语言描述该三角形边角间具备怎样的联系.

在这个问题的引导下，学生很快提出该三角形有两个底角相等，存在一个直角，其中有两条边也是相等的.如图1，在文字语言的描述下，将问题抽象为数学条件：△ABC中，∠C=90°，BC=AC，∠A=∠B.

教师充分肯定学生的发现，并着重强调该三角形的类型，由此揭露本节课复习的主题为“全等三角形”.并要求学生结合自身已有的学习经验，回顾全等三角形的性质与判定方法.

学生自主回顾并总结，提出全等三角形的判定方法分别有如下五种：SAS，AAS，SSS，ASA，HL.

设计意图 该阶段学生对等腰三角形还处于一知半解的状态，因此并不能理解等边对等角与等角对等边的性质，借助三角板这个等腰直角三角形作为课堂导入的素材，带领学生提炼出此类三角形所具备的基本条件，为本节课的复习教学奠定了基础. 同时，通过回顾全等三角形的判定方法，一方面揭露复习主题，另一方面为接下来的课堂教学做好铺垫.

2. 编题探索判定方法

编题探索一

教师在课堂上展示一根戒尺与一个等腰直角三角板，让学生感知这两种常见的几何图形，并将戒尺上的一点置于三角板的直角顶点C上，保持接触点不变的情况下任意旋转戒尺，观察戒尺与三角板之间存在怎样的位置关系. 要求学生自主在草稿纸上画出三角板ABC与戒尺NM的位置关系.

学生自主画图，教师巡视并点拨，从学生所画图形中选择MN过线段AB的中点D（见图2）的情况加以投影展示. 要求学生根据这幅图自主编拟问题并解答.

生1：如果点D为线段AB的中点，那么就能通过SSS明确△ADC≌△BDC.

师：很好！根据“点D为线段AB的中点”这个条件，还可以获得什么结论？

生2：根据这个条件可以推断出AD与DC之间为垂直的关系.

教师又提出：若将AD⊥DC视为本题的已知条件，可推导出什么新的结论吗？

在这个问题的启示下，学生很快得出“CD为∠ACB的角平分线”的猜想，具体证明过程略.

设计意图 选择MN与AB相交这一特殊情况加以探索的灵感源自等腰三角形“三线合一”的性质，实物的展示与旧知的回顾拉近了学生与知识的距离，让学生感知全等三角形判定定理并不复杂，这种相对简单的边角关系能让学生快速获得其中的等量关系.当然，随着条件的转化，问题也会发生改变，那么形成的问题则更丰富.

编题探索二

师：以上探索过程，我们选择了一个非常特殊的情况，即直线与中线相重合的情况，接下来我们继续旋转戒尺，来探索MN旋转到三角板外部之后的情况.如图3，在增加两个垂直条件的基础上，我们来探索图形间具有怎样的联系.

在教师的启发下，学生很快就通过自主画图获得了两个全等三角形.在此基础上，教师鼓励学生自主分析线段DE，BE，AD之间具有的关系.有学生很快就举手表示，用直尺度量法，可发现DE=BE+AD.

教师对该生的探索方法给予肯定，并表示此为测量获得的结论，属于猜想类别，是否准确还需加以证明，并要求学生自主证明该结论的正确性.

生3：根据同角的余角必然相等，获得∠DCA=∠EBC，根据AAS可确定△EBC≌△DCA，由此可知CD=BE，CE=AD，所以DE=BE+AD.

师：非常好！现在我们继续旋转戒尺，让MN落于△ABC的内部，由此可获得怎样的结论？

对于这个问题，学生自主画图（见图4）并分析，提出“DE=AD-BE”的结论.

以上探索过程可抽象为如下数学问题：已知△ABC中的AC，BC相等，∠ACB为直角，且AD，BE分别与直线MN垂直.请证明：①△ADC≌△CEB；②DE=AD+BE；③DE=AD-BE.

设计意图 通过实操活动提炼数学问题，不仅促使学生掌握AAS判定定理，还促使学生从“K型图”中转化线段关系，由此对线段之间的和与差关系形成进一步的认识.

编题探索三

师：若将戒尺围绕点A旋转，又能编拟出怎样的问题呢？首先来观察MN落于△ABC内部的情况，即戒尺为角平分线时，AB，AC，CD之间会有怎样的关系？

生4：这三者之间的关系为AB=AC+CD.

师：能描述得更具体一些吗？

生5：如图5，当AD为∠CAB的角平分线时，过点D作ED⊥AB，E为垂足，根据这些条件可求证AB=AC+CD.

师：还可以如何描述该辅助线？

生6：在线段AB上截取AE=AC，再将DE连接起来，此为截长法；也可以将AC延长至点F，令FA=AB，再将DF连接起来，此为补短法.

师：很好！这两种方法的应用，均为了借助辅助线分析线段之间和差关系问题，其中作垂线段属于特殊的截长法.那么此探索过程以数学形式编拟问题，该如何呈现？

生7：已知△ABC中的∠ACB为直角，AC=BC，AD为∠BAC的平分线，求证AB=AC+CD.

设计意图 先猜想结论，而后再编题，有效降低了问题的难度，给学生的思维提供了明确的方向.这种教学方法，不仅让学生能直接通过测量法获得结论，还让学生在解题过程中感知截长法、补短法的实际应用，明确截长法包含了作垂线段.

编题探索四

如图6，在教师的引导下，学生编拟出来的问题为：已知△ABC中，∠ACB为直角，AC=BC，BD=CD，求证：2AD<AB+AC.

设计意图 该环节同样是求证猜想结论的过程，受思维定式的影响，有些学生会考虑借助刻度尺来分析结论，殊不知，此类问题只要掌握“倍长中线”的作法，就能借助补短法顺利解决问题.

3. 总结提炼发展能力

教师要求学生基于整体的视角回顾本节课所编拟的几道试题，提出判定三角形全等的条件有哪些，添加辅助线的方法有哪些，判定过程中涉及的数学思想方法有哪些等问题.