核心素养背景下初中数学渗透数学文化的策略研究

［ 摘 要 ］数学文化是记录与传播数学思想的重要方式，也是传递信息的主要载体.将数学文化渗透在“三角形内角和定理”的证明教学中，一方面，有助于深化学生对证明方法的认识，并激发他们的学习热情；另一方面，能有效促进学生的数学核心素养的发展.

［ 关键词 ］核心素养；数学文化；数学史

数学文化是人类智慧的结晶，它以独特的方式保留并记录了特定阶段的数学发展史 . 将数学文化有机地渗透在初中数学课堂中，不仅能激发学生对新知的探索兴趣，还能进一步发展学生的数学思维，提升学生的关键品质，培育学生的综合素养 .“三角形内角和定理”的孕育与成长历程丰富多彩，历史上诸多数学家的验证方法并未因岁月的流转而失去光彩，反而如同陈年佳酿，在时间的长河中愈发醇厚，闪耀着智慧的光芒 . 将这些史料渗透在课堂中，可发展学生的核心素养.

教学过程设计

1.新课引入

借助多媒体展示形状大小不一的若干个三角形，要求学生说一说这些不同三角形具有怎样的共同点.生 1：所有三角形都具备的特点有：①两条边之和大于第三条边；②两条边之差小于第三条边；③内角和为180°.

师：不错 . 对于平面几何的探索，通常从边和角这两个维度入手.关于三角形的三边关系，以前已经探索过.本节课，我们共同探讨“三角形的内角和恒为180°”的几何原理.有什么办法可以确定三角形的内角和为180°呢？

生 2：可以用量角器直接测量每个角的度数，将三个角的度数相加即可明确三角形的内角和为180°.

生3：通过拼图法同样能验证，即将三角形的三个角都截取下来，拼在一起形成一个平角.

师：众所周知，人们亲眼所见的事物并非是真实的，大家所提的度量法或拼图法也不能说明三角形的内角和一定为180°.那么，我们究竟该如何准确判定呢？

生（众）：用证明法.

师：不错，严谨的证明能够阐释一切.每个人的思维方式不一样，证明方法也各有特色.接下来，咱们就一起探索具体的证明方法吧.

设计意图 借助多媒体展示不同的三角形，旨在引导学生探寻其共同的特征，此为研究数学问题的重要方法之一.学生从多种图形中得到恒定不变的结论，不仅唤醒了对三角形边角关系的认知，还思考并尝试运用多种不同的方法来证明三角形的内角和为180°.

2.证法探究

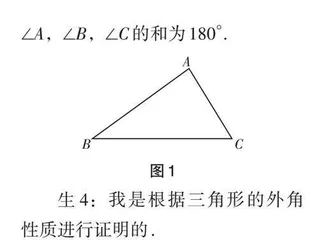
问题：如图 1，已知 ∠A ， ∠B ，∠C 为 △ABC 的三个内角，请证明∠A，∠B，∠C 的和为180°.

生 4：我是根据三角形的外角性质进行证明的.

交流后发现，该学生所述的外角性质是基于三角形内角和为180°的推论，属于一种循环论证，显然这种证明方法不可取.

生5：如图2，过点 A 作 CB 边的平行线，因为平角等于180°，所以∠A，∠B，∠C 的和为180°.

师：太棒了！你用毕达哥拉斯学派的证明方法获得了三角形内角和的度数 . 你是怎么想到这种方法的？

生 5：若两直线平行，则内错角必定相等 . 我是通过这个性质想到的.

师：生 5 将三角形三个离散的角聚集在一起形成平角而获得三角形内角和的度数，这个过程主要采用了平行线转换角度的方法.简单来说，就是“由果索因”，这是找到基本证明思路的好方法.当然，还可以通过分析已知条件或引入辅助线的方法逐步推导出“果”，利用“由因推果”的思路解题.

师：生 5 的证明方法带给了我们一些启示，即证明过程要“有理有据”，即从理性的角度来分析问题 . 一般情况下，真命题被称为定理，这是用来证明其他命题或进行运算的重要依据之一.本命题还有其他证明方法吗？

生 6：我联想到了平行线同旁内角互补这个定理.

师：这也是“由果索因”的思路 . 按照这个思路，我们应怎么证明呢？

生6：如图3，过点A作BC边的平行线，根据“两直线平行，同旁内角互补和内错角相等”证得△ABC的内角和为180°.

师：非常好！此为18世纪克莱罗提出的证明方法.

生 7：我的证明方法与前两位同学都不一样.

师：哦？具体说说.

生7：如图4，过点C作 AB 边的平行线，由两直线平行确定同位角、内错角相等，证得 △ABC 的内角和为180°.

师：不错，此为欧几里得记载在《几何原本》中的证明方法.

设计意图 学生按照自己的想法来证明问题，结果发现和数学家们的证明方法是一样的.学生惊觉自己竟然能与数学家的思维产生共鸣，这让他们感到无比骄傲和自豪.经由师生间活跃的互动，学生的潜在思维逐渐显化.辅助线的制作不仅体现了“由果索因”与“由因推果”的思路历程，还引领学生达到了“知其然且知其所以然”的境界，从而有效推动了学生逻辑推理能力和数学思维能力的发展.历史上，数学家们提出的证明方法，深刻地融入了数学文化的精髓，引领学生领略数学古今交融的魅力.

3.古今融通

在两千多年前，聪明的人们就发现了三角形内角和为180°这个结论 . 为了更生动地展现这一数学奇迹，教师借用短视频精彩演绎以下内容：泰勒斯从拼图中发现了端倪，帕斯卡在折叠中获得了启示，提波特在旋转中获得了结论，毕达哥拉斯学派以及诸多数学家用多种方法证明了三角形内角和为180°.

师：泰勒斯从拼图中发现了端倪，并验证了猜想，为何提波特和帕斯卡等人还要用不一样的方法来验证这个结论呢？而且后来仍有大量的数学家去追求更多的证法.这些现象体现了什么？

在上述问题的启迪之下，学生自主提炼出“探索”“严谨”“钻研”“创新”及“挑战”等关键词汇，这些词汇共同体现了理性思维的深化与积极信念的树立.

设计意图 数学的发展历经了悠长的岁月，通过小视频向学生传播数学史，不仅能够增添课堂的趣味性，拓宽学生的视野，还能激励学生主动从多样的证明方法中提炼出“利用平行线转换角度”的共通之处.同时，此举也极大地促进了学生数学思维的发展，为培养学生逻辑推理素养奠定了坚实的基础.学生在证法探究环节积极运用了多位数学家的经典证明方法，这不仅激发了他们对数学发展历程的独到见解，还使他们在深入探索多种证法的过程中，对数学的本质有了更深刻的认识.

4.应用新知

想要让学生真正理解新知，最佳途径莫过于将所学知识付诸实践.

题 1 如 图 5， 已 知 ∠DCA 为△ABC 的一个外角， ∠A ， ∠B 的度数分别为 70°，40° ，那么 ∠DCA 的度数是多少呢？

题 2 若直角三角形的一个锐角度数为 35° ，那么该直角三角形的另一个锐角度数是多少？

题 3 如图 6，已知线段 AC 与BD 于 点 O 处 相 交 ， 请 证 明 ∠A +∠B = ∠C + ∠D .

题 4 如果一个三角形的三个内角度数之比为 5 ∶ 2 ∶ 2 ，那么这个三角形的三个内角度数分别是多少？

设计意图 前两道题目以定理作为运算依据，通过角度数的变化引导学生自主发现并描述结论，从中提炼出特殊到一般的数学思想.后两道题目，一方面凸显定理在推理中的作用，另一方面揭露定理亦可作为构造方程相等关系的依据.

5.总结提升

师：通过本节课的学习，大家觉得哪些思想方法可以帮助我们确定一个命题是正确的？

生8：作辅助线来证明.

生 9：用“由果索因”或“由因推果”的思路来证明.

生10：用转化思想来证明.

……

师：当你看到“证明”二字时，首先映入脑海的是什么？生11：定理、周密、公理、严谨、言必有据等词语.

生 12：我想到的是“由因推果”以及“由果索因”.

生13：不能循环论证，论证方法应具有多样性.

师：很好！“证明”是本节课教学的关键词.经过本节课的探索，同学们对证明过程与技巧有了更为丰富且深刻的体验.关于同一个问题有多种证明方法的探索，给你们带来了什么启示？生14：多种巧妙的证法，让我对三角形的内角和有了更为深入透彻的理解，仿佛瞬间豁然开朗，茅塞顿开.

生15：我发现，要证明一个问题，关键在于精准地把握其核心要点，例如本节课就紧扣“180°”展开探索.

生17：我发现，数学是一门又美又有文化的学科，我们所探索的证明方法竟然与历史上数学家们的证明方法一致，太神奇了！这让我对数学学习更有信心了.

生18：是啊，是啊！我都觉得自己成了数学家（大家笑）.

生19：通过本节课的学习，让我充分感知了人类的探索与创新精神，尤其是各种数学思想方法的应用，增加了数学的魅力.

从学生的课堂反馈来看，本节课的学习让学生对数学证明产生了浓厚的兴趣与信念.这不仅为学生增添了学习动力，更为他们日后的个人发展奠定了坚实的基础.

教学思考

1.以史为纲，灵活渗透

为了促使学生在学习过程中更加关注数学史，教师需要自身对数学史有深入且全面的了解.在备课阶段，教师可有针对性地搜集与教学内容相关的数学史料，从中挑选出符合教学实际的内容有机地渗透到课堂中.本节课，三角形内角和的形成历程颇为丰富，众多数学家参与其中.尽管教师无法在课堂上详尽讲述每一个“小故事”，但可以巧妙地结合学生在课堂上的思考路径，适时地引入证明方法的典故.这样做不仅能在一定程度上鼓励和认可学生的思维能力，还能有效增强他们学习的自信心.

2.以史为鉴，辨析证法

同一个问题可能存在多样化的证明方法，有些方法在历史的长河中永盛不衰，它们为当今的课堂注入了丰富的教学素材与深刻的启发 . 想要让学生在课堂学习中不仅掌握知识，更能深入理解其背后的原理，最佳途径便是激发学生的思维活力，为他们打造一个开放的探究空间 . 本节课的“古今融通”环节，教师利用小视频的形式，向学生生动地展现了三角形内角和的历史探索之旅，不仅让学生深刻体会到了数学家们严谨治学、不懈探索的精神风貌，还为学生敲响了警钟 — —在面对证明类问题时，务必谨防循环论证的陷阱 . 这种以史为镜的教学策略，能成功启发学生的辩证思维，促使学生理性观察每一件事物.

3.以史为泉，发展素养

课堂上能渗透的数学史有限且浅显.若想进一步渗透数学文化，发展学生的数学核心素养，教师可以课堂为契机，引导学生将对数学史的了解延伸到课外.如本节课所呈现的帕斯卡折叠与提波特旋转等内容尚显浅显，教师可激励对此有浓厚兴趣的学生，在课后自主深入探究折叠与旋转的奥秘，以此锤炼实践技能，进一步培育核心素养.

总之，数学文化能够有效激发学生对数学的浓厚兴趣.事实证明，古今交融，为课堂注入了智慧与人文的活力，这正是新课改背景下课堂的理想追求.