基于“做数学”的初中数学教学实践研究

[摘  要] “做数学”是学生在教师的指导下通过操作体验、数学实验和综合实践，形成系统的、结构化的数学知识，从而真正享受完整的数学学习过程的一种学习方式. 有数据表明， “做数学”能促进学生深度学习. 在“做数学”的过程中，学生积极主动地参与了数学知识的发生、发展和形成过程，因此，“做数学”有助于学生理解和领悟数学思想、知识和方法，有利于激发学生的学习主动性与积极性，从而发展学生的数学思维，促进学生深度学习的发生.

[关键词] “做数学”;初中数学;教学实践

问题提出

一直以来，急功近利的数学教育观念，致使义务教育阶段数学教学普遍存在过程形式化、目标功利化的问题，学生的感官在数学学习过程中并未得到充分调动，学生的思维并未得到充分激活，学生的情绪难以获得正面输出. 基于以上问题，受到欧美广泛推行的“hand-on”学习计划的影响，以陶行知“教学做合一”和杜威“从做中学”的教育思想为理论基础的“做数学”，越来越受数学教育工作者重视[1]. 学生学习数学不该只是记、背、练、考数学，而应该是“做数学”. “做数学”可以让学生在“做”的过程中，经历知识的产生过程、丰富知识的表征方式、触及知识的基本原理，有利于抽象的数学知识直观化、可视化. 可见，“做数学”是促进学生深度理解知识的重要学习方式. 因此，本文基于“做数学”的视角，结合教学实践阐述基于“做数学”的教学实践的实效，从而打造基于“做数学”的课型范式.

理论基础

1. “做数学”

“做数学”是学生在教师的指导下进行操作体验、数学实验和综合实践，在“做”的过程中积累丰富的直接经验，在教师的有意识指导下自主归纳和总结数学概念、数学规律，并进行加工概括，将所学的数学知识整理成数学公式或数学命题，力求形成系统的、结构化的数学知识体系，从而享受完整的数学学习过程的一种学习方式. 在“做数学”的学习过程中，学生主动参与数学知识的发生、发展和形成过程，有助于理解和领悟数学思想、知识和方法，有利于激发学生的学习主动性与积极性，从而发展学生的数学思维，促进深度学习的实现.

“做数学”的学习过程如图1所示.

2. 深度学习

深度学习致力于激发学生的内在学习动机，通过设置引领性学习主题、挑战性学习任务或活动以及持续性的学习评价，吸引学生积极主动地、全身心地投入学习活动中，感受学习的乐趣，体会学习的价值与意义，不断生成成就感和效能感，进而达到为理想和热爱而学习的境界. 深度学习具备如下五个特征：活动与体验，本质与变式，联想与结构，迁移与创造，价值与评判. 研究认为 “做数学”有利于促进学生深度学习，因为学生在“做数学”的过程中经历探究历程，激活高阶思维;贯通思想方法，掌握知识本质;顺应原有认知，把握知识脉络. 进而激发学生深层质疑，发展深度思维，最终实现深度学习.

基于“做数学”的教学实践实例

基于“做数学”的教学实践主要是通过操作体验、数学实验和综合实践来实现手脑协调、启思明理的目的. 下面分别从操作体验、数学实验和综合实践三个角度利用课堂实例（如表1所示）说明平时初中数学教学如何设计基于“做数学”的教学.

1. 操作体验

操作体验主要表现为通过具体的操作，使得数学概念或运算法则具体化、形象化，为进一步抽象概念或者提炼运算法则奠定基础[2]. 操作体验活动能让抽象可视化，能赋予抽象运算直观上的意义，从而激活创新意识.

例如，教学八年级上册“三角形的内角和公式”时，教师设置动手操作环节：通过量一量、剪一剪、拼一拼、折叠等操作活动，引导学生经历三角形内角和的探究过程;通过剪拼，将三个角拼成平角180°，从转移两个角（分为同侧和异侧两种情况）到转移三个角（可以转移到三角形的内部、外部和三角形的边上），为学生证明三角形的内角和定理提供证明思路，培养学生观察、思考、分析、解决问题的能力.

又如，教学七年级下册“点、线、面、体”中的“认识几何体”时，教师设置了两个触感活动. 活动1，袋子中装有若干个几何体模型，请学生从袋子里摸出指定的几何体，并拿给其他同学看，看谁找得快，并说说是怎么找到的. 活动2，请两名学生合作完成以下活动：一名学生摸着一个几何体模型，向另一名学生描述这个几何体的特征（用数学语言精准且有条理地表达），另一名学生则根据描述说出该几何体的名称. 两名学生交替进行此活动. 通过这两个活动，学生将触感转化为了数学语言，既有助于提高学生的数学语言表达能力，又有利于培养学生的空间想象能力.

再如，教学八年级上册“整式乘法运算”时，教师让学生自备若干正方形、长方形，并引导学生根据乘法公式将图形进行分割、拼接——由数到形，接着利用正方形、长方形拼凑出可证明乘法公式的图形——由形到数. 可见，设置活动能让抽象的数学公式可视化，能赋予抽象运算直观上的意义，从而激活学生的创新意识.

2. 数学实验

数学实验旨在通过操作探究、发现证明等方法来学习数学. 数学实验是指学生在教师指导下，利用一定的数学工具（实物或几何画板软件），通过动手操作、观察思考、归纳抽象等过程尝试建构数学概念，验证数学结论，进而探索数学规律，最终解决数学问题的一种学习方式.

例如，教学八年级下册“一次函数的图象与性质”时，教师通过软件（几何画板）加密点，来猜想一次函数的图象，使得教学过程更加直观、明了;通过追踪点，来验证对一次函数图象的猜想. 可见，数学实验能让数学学习更加直观有效，有利于排除学生的思维障碍，有助于培养学生严谨的科学精神，让学生的数学学习更加生动有趣.

又如，教学“‘标记法’：池塘里有多少鱼？”时，要解决这个问题，教师可以引导学生思考以下问题：一个瓶子里装满了黄豆，请问可以用什么方法估计出瓶子中豆子的数量. 为了解决这个问题，学生决定动手实验. 可见，数学实验能将原本难以操作和实践的问题转化为可操作、可视的数学实验，且学生在数学实验的过程中可以重新认识自己，并重构数学知识结构.

3. 综合实践

综合实践，即通过实践、思考、运用、解决问题来学习数学. 综合实践是以学生的经验与生活为核心的实践性课程，强调学生通过实践活动，增强探究和创新意识，从而发展学生综合运用知识的能力. 综合实践是以实际问题为载体，以学生自主参与为主的学习活动. 学生在综合实践活动中会充分调动各个感官：动脑、动手、动口，从而全身心地投入其中[3].

例如，教学九年级下册“相似三角形的应用”时，教师设计了“室外测量一棵大树的高度”这一活动，从课前工具准备、现场实际问题解决以及数学知识的应用中，学生的学习兴趣被极大地激发了，这有助于学生理解和把握数学思想、知识和方法，能进一步发展学生综合运用知识的能力.

4. 以“圆周角定理”为例，设计基于“做数学”的教学实践范例

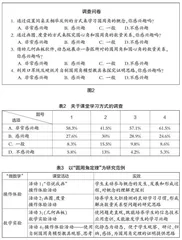
“圆周角定理”的课程内容是理解圆周角的概念，探索圆周角及圆周角所对弧的关系，了解并证明圆周角. 学习本节课之前，教师进行了一次问卷调查，主要是调查学生更感兴趣的课堂学习方式. 本调查选取的是×中学的450名九年级学生. 本次调查共发放问卷450份，收回450份，有效问卷435份，有效率约96.7%. 本次调查问卷的内容如图2所示，结果如表2所示.

调查结果显示，有58.3%的学生对第1题中的学习方式非常感兴趣;有41.5%的学生对第2题中的学习方式非常感兴趣;且对比第一题和第二题中的学习方式，学生更倾向于同桌互动这一学习方式. 有57.1%的学生对第3题中的学习方式非常感兴趣，有61.5%的学生对第4题中的学习方式非常感兴趣，可见，学生对几何画板、自制教具等化静态模型为可视化动态模型的学习方式情有独钟.

于是，教师根据课程内容及问卷调查结果，设置了基于“做数学”的四个学习活动（如表3所示）.

活动1：“你说我画”操作体验活动

“你说我画”活动，即类比圆心角的定义给圆周角下定义：一名学生用自己的话描述什么是圆周角，另一名学生根据描述尝试画出反例，两名学生在不断纠正概念的过程中最终得到正确且简洁的圆周角定义. 通过动手、动脑、动口的操作体验，学生主动参与圆周角概念的发生、发展和形成过程，对数学概念的理解更加深刻.

活动2：画图、度量等操作体验活动

任取弧AB，画出它所对的圆心角∠AOB和它所对的圆周角∠ACB. 观察并测量∠ACB与∠AOB. 小组讨论结果，并说说猜想. 教师引导学生学会通过画图、观察、度量、归纳等操作体验，去探究数量关系型问题，在操作中感悟实践出真知. 通过活动，培养学生动手参与操作、自主探索、大胆猜测的良好学习习惯，从而形成解决数量关系型问题的研究思路.

活动3：（几何画板）数学实验活动

教师指导学生融合信息技术，借助几何画板软件，动态地展示一条弧所对的圆周角和圆心角的数量关系，以验证数学猜想. 通过几何画板（数学实验）来验证数学结论，能使问题更加形象、直观，能培养学生的信息技术应用意识，还能激发学生的学习兴趣.

活动4：操作体验活动——使用自制圆周角模型教具观察、思考

证明圆周角定理时，利用口罩绳及硬纸片自制圆周角模型教具，引导学生亲自操作体验，感受数学是可操作的、可视的. 学生在操作中观察、研讨、归纳，感悟证明圆周角定理的关键是分类讨论思想，从而为圆周角定理的证明提供思路.

教育家苏霍姆林斯基说过：“手和脑之间有着千丝万缕的联系，手使脑得到发展，使它更加明智. ”因此，在数学知识的学习过程中，教师要引导学生动手操作，如拼一拼、折一折、剪一剪、量一量、画一画，要给学生提供尽可能多的动手、动脑、动口机会，从而激发他们参与学习的兴趣，使他们乐学、善学.

价值与反思

基于“做数学”的教学实践既是一种重要的数学学习方式，也是学生进行有效数学学习的一种重要途径. 教学初中数学时，教师要认识到“做数学”能够优化数学探究，使问题得到解决，并促进深度学习实现. 基于“做数学”的教学实践的显著价值在于，能培养学生的实践能力和创新精神，能推进教与学方式的改革.

1. 培养学生的实践能力和创新精神

教师常常因自己对学生心理认知的缺失而低估学生的创造力，并会在无意间扼杀学生探索新事物的兴趣和热情的天性. 在“做数学”的过程中，教师设计的一系列动眼观察、动手操作、动脑思考的实践活动，能引导学生自主获取所需的“事实”（基本概念），进一步领悟概念的本质;“做数学”的过程能延长知识的获得过程，能给学生提供足够多的感悟知识的时间和空间，从而让学生获得“如何思考”的智慧. 特别是处于基础地位的概念、原理的学习，更强调让学生通过动手“做数学”来获得亲身感悟，从而经历“感知—感悟—知识”的过程，使得学生最终获得的不只是知识，还有智慧[4]. 因此，基于“做数学”的教学实践有助于培养学生的综合实践能力和创新精神.

2. 推进教与学方式的改革

基于“做数学”的教学实践是一种体验式学习方式，学生在“做数学”的过程中可以获得抽象数学概念、数学原理的直接体验. 通过“做数学”，学生不仅经历了数学对象的要素、数学概念的内涵的抽象过程，数学法则、性质、定理、公式等的归纳和发现过程，而且会产生“如何研究”“如何发现”的方法论感悟. “做数学”改变了传统的接受式学习方式，同时对教师的教学方式提出了极大的挑战，所以教师要改变以往“满堂灌”的教学方式，要重在引领，做一位合格的领路人. 因此，基于“做数学”的教学实践能推进教与学方式的改革，能使数学知识成为学生自己发现的结果，并有助于学生对数学知识的理解，对数学思想方法的领悟[4]，从而促进学生数学核心素养的发展.

参考文献：

[1]章建跃. “做数学”的育人价值探讨[J]. 教育研究与评论，2021（03）：27-29.

[2]章建跃. 课程改革呼唤数学实验[J]. 江苏教育，2017（27）：18.

[3]郭庆松. 做数学：思想渊源与课程实施[J]. 教育研究与评论，2022（02）：38-43.

[4]郭庆松. 在“做数学”中促进深度理解[J]. 教育研究与评论，2021（03）：30-35.

基金项目：福建省教育科学“十四五”规划2022年度课题“基于‘做数学’的初中数学深度学习教学实践研究”（FJJKZX22-295）.

作者简介：李雅云（1988—），硕士研究生，一级教师，从事中学数学教育研究工作.