生本理念下的“趣动数学”课堂教学模式探微

[摘  要] “趣动数学”课堂作为一个教学主张，教师主要致力于教学模式的研究. 教师构建“问题情境激兴趣—活动探究增乐趣—展示释疑生理趣—反馈提升培志趣”的教学模式，用外在的“动”去激发学生内在的“趣”，进而让学生真正成为课堂的主人，使生本理念落地生根.

[关键词] 趣动数学;教学模式;生本理念

“趣动数学”作为一个教学主张，教师主要致力于教学模式的研究. 我们提出通过设置问题、组织活动、充分展示、及时反馈等外在形式，给学生提供足够的时间和空间，以提高学生数学课堂的参与度和投入度，用外在的“动”去激发学生内在的“趣”，这里的“趣”指从兴趣、乐趣到理趣和志趣，进而让生本理念真正落地生根. 本文以（人教版数学七年级上册）“3.4 实际问题与一元一次方程”一课为例，进行“趣动数学”课堂教学模式的粗浅探讨.

教材分析

在知晓一元一次方程的定义、学会一元一次方程的解法基础上，本课将利用一元一次方程解决实际问题. 教材共有两道例题，分别为调配问题和工程问题，后续还有三个探究问题，分别涉及销售盈亏、球赛积分和电话计费. “一元一次方程”是初中方程大类中的起始章节，后面的“二元一次方程组”“分式方程”和“一元二次方程”，以及函数大类问题，都离不开实际问题，学生对本节内容的掌握程度将直接影响后续知识的学习效果.

备课思考

学生在小学阶段已经接触过一元一次方程，他们会用算术方法和方程思想解决实际问题，知道列方程解应用题的一般步骤. 但是小学里的应用题比较简单，数量关系一目了然，有时仅凭记忆一些常见题型就可以让问题得到解决，而本课的应用题较为复杂，数量关系不够直观，需要一定的理解能力和分析能力的加持. 怎样把已知条件分析透彻，找到正确的等量关系，是本课需要解决的问题. 为了让学生进行深入研究，我们把两个例题拆分为两节课，本节课主要研究工程问题. 教材中的例题，是比较复杂的工程问题，学生根据小学的学习经验，知道工程问题中三个基本量之间的数量关系，即工作时间×工作效率=工作量. 本例中，工作时间已经直接给出，具体的工作量缺失，工作效率则需要一定的分析能力才能获知，如果让学生直接解决此题，难度较大，学生会产生畏难情绪. 而工程问题又是初中应用题的典型题型，必须掌握. 基于以上思考，教师创设了一个真实的问题场景，通过不断变式，由易到难，层层递进，各个击破，使学生在解决问题的过程中，找到解决问题的方法，实现知识的螺旋式上升. 教师教学的重点是列一元一次方程解工程类应用题;难点是理清工程问题中的各种量，学会寻找列一元一次方程所需的相等关系. 学生的学习目标为：（1）会用数学的眼光观察实际问题，并会转化成恰当的数学问题，培养模型观念;（2）掌握用列表法分析工程问题;（3）经历从人员分工和先后顺序两个不同的角度分析工程问题的过程，体验方法的多样性;（4）在解决问题的前提下，尝试自主提出有意义的工程问题;（5）在与同伴合作交流中，体会合作的乐趣，在参与数学活动中，经历独自克服困难、解决数学问题的过程，获得成功的体验，培养学好数学的信心.

教学流程

（一）问题情境激兴趣

问题：已知某泳池有3根进水管、2根出水管，且1根进水管工作15小时可以将空泳池注满，1根出水管工作24小时可以将满池的水放完. 现在要注满空的泳池，由于工作人员的疏忽，5根水管先同时打开2小时后，才关闭2根出水管，则注满泳池还需要多少时间？

设计说明  在小学，学生已经接触过一些基本的应用题，常见的有工程问题、进出水问题、鸡兔同笼问题等，本课开门见山提出这个问题，目的是迅速吸引学生的注意力，同时激发学生的学习兴趣. 这个问题有一定的难度，不需要学生马上解决，后续引例的呈现，将给学生提供心理和思维双重准备. 同时，这个问题的设置，也为优秀的同学提供了展示自我才能的机会. 史蒂芬·柯维在其著作《高效能人士的七个习惯》中提到，“最好的学习方法就是教会别人”，用怎样的方法使同学们听懂自己的思路，理解方法的合理性，将成为他们本节课学习的目标.

引例：

1. 为构建书香校园，学校图书馆新购置了3600本图书，交给甲、乙两个班级先后接力完成整理工作，共用时20小时. 已知甲班每小时整理240本，乙班每小时整理160本. 求甲、乙两班整理图书分别用了多少小时.

归纳：列一元一次方程解应用题的一般步骤.

2. 整理一批图书，甲班单独做需要10小时，乙班单独做需要15小时. 现两班合作，需要几小时？

回忆：工程问题的数量关系.

设计说明  以上两道引例，都是学生小学做过的工程类基本问题，引例1用来回顾列方程解应用题的一般步骤，让学生知道小学所列的方程其实就是我们现在所学的一元一次方程，实现了小学与初中知识的无缝衔接. 引例2与引例1相比，没有具体的工作量，工作效率也没有直接给出，以此唤醒学生对小学工程问题的记忆. 解决此类问题，我们通常将工作量记为“1”，这样工作效率就可以表示出来了. 此题主要用来回忆工程问题中三个基本量之间的数量关系. 以上设计，能将学生已有的旧知激活，为本课新知的探究做好铺垫.

（二）活动探究增乐趣

变式1：整理一批图书，甲班单独做需要10小时，乙班单独做需要15小时. 现甲、乙两班合作4小时后，剩下的部分由乙班单独做，还需要几小时才能完成？

活动要求：

（1）学生独立思考，列方程并求出答案;

（2）想一想还有没有其他方法;

（3）学生以小组为单位，组长组织组员先校对答案，再分享思路;

（4）各学习小组推荐一名同学，介绍小组的求解方法.

引导：教师引导学生借助表格分析题中的已知条件，进而得出相等关系.

设计说明

（1）学生在小学阶段就接触过工程问题，问题难度不大，也可以用算术方法求解. 每个学生的学习基础有差异，分析问题的角度不同，解决问题的方法也各异. 教师要求学生在独立思考的基础上组内分享方法，既保证了个人认真思维，又能与同伴进行碰撞，启发思维. 小组活动形式，则增强了学习乐趣，激发了学生的学习热情.

（2）解应用题最关键的是寻找相等关系，这个寻找的过程就是突破本课难点的过程. 在小组介绍方法的时候，教师要有意识地进行追问，将学生所表示的量写在表格中对应的位置，先形成按照人员分析的第一张表格，再由教师主动给出１/10+1/15和1/15，引导学生自主写在对应位置，形成按照先后顺序分析的第二张表格，最后让学生观察表格，发现相等关系，体会表格的作用. 这个环节的设计可以看成是突破难点的第一步：初步感知用列表法可以让条件更直观.

（三）展示释疑生理趣

编题：整理一批图书，甲班单独做需要10小时，乙班单独做需要15小时. _________________，还需要几小时？

由学生自编题目，其他学生共同解决.

学生编题如下：

1. 整理一批图书，甲班单独做需要10小时，乙班单独做需要15小时. 两班合作4小时后，剩下的部分由甲班单独做，还需要几小时？

2. 整理一批图书，甲班单独做需要10小时，乙班单独做需要15小时. 甲班单独做4小时后，乙班来与甲班合作，还需要几小时？

追问：以上的编题，不变的是什么？改变的是什么？怎样分析问题？

提炼：在这样的问题背景下，如果从人员方面来分析，无论怎样改编，我们都可以看成是在改变工作时间;如果从先后顺序方面来分析，则可以看成既改变工作效率，又改变工作时间，所以，只要借助表格，分析清楚这两个工作量，则万变不离其宗，都可以用同样的相等关系来列出方程.

设计说明  按照建构主义理论，学生学习的过程就是对知识进行自主建构的过程. 要编题成功，学生就要对实际问题的意义有清晰的认识，同时编题还需要考虑是否符合实际意义. 后续的提炼则是列表法从被动接受到主动运用的过程，是将列表法纳入自己已有知识结构的过程. 学生通过展示释疑，感受数学独有的理性思维的魅力. 这个环节的设计可以看成是突破难点的第二步：工程问题中三个量的正确表示.

例题：整理一批图书，由一个人做要40小时. 现计划由一部分人先做4小时，然后增加2人与他们一起做8小时，以完成这项工作. 假设这些人的工作效率相同，那应先安排多少人工作呢？

要求：分别按照先后顺序和人员分工来分析，并完成表格填写.

归纳：解决本例题的关键是用整体思想分析工作效率.

设计说明  前面问题的难点在于列表法的初步运用，以及三个量的表示，本例题则侧重于对工作效率进行探究. 经探究后发现多人的工作效率=1人的工作效率×人数，所以这个例题的设计可以看成是突破难点的第三步：用整体思想表示题中的量.

（四）反馈提升培志趣

1. 解决问题：

已知某泳池有3根进水管、2根出水管，且1根进水管工作15小时可以将空泳池注满，1根出水管工作24小时可以将满池的水放完. 现在要注满空的泳池，由于工作人员的疏忽，5根水管先同时打开2小时后，才关闭2根出水管，则注满泳池还需要多少时间？

引导：本题两种水管的工作效率有本质的区别，怎样来表示这个区别呢？

设计说明  首尾呼应，回到课堂起始阶段提出的问题. 这道题是本节课所学方法的拓展和提升，它和前面探究的问题不同，前面涉及的相等关系都是工作量的和，这里是工作量的差. 当然，若把其中一个工作量用负数来表示，则仍可以看成工作量的和. 教学时教师要让学生充分意识到，数学学习不是简单地生搬硬套，务必在理解的基础上，真正内化成自己的知识和方法，这样才可能正确地迁移和运用. 同时，解决这样的实际问题，还能培养学生学好数学，为社会做贡献的志趣.

2. 课堂小结：

梳理本节课的收获和体会，回忆本节课的探究历程，思考本节课的疑难和困惑.

3.目标检测：

（1）一项工作，甲单独完成需要4天，乙单独完成需要6天，现由乙先做1天，剩余部分甲、乙合作. 问：剩余部分甲、乙合作还需多少天？若完成工作后共获得报酬3600元，且按各人完成的工作量计算报酬，那么该如何分配？

（2）一个水池有进水管甲和出水管乙，单独开放甲水管10分钟可以注满水池，单独开放乙水管15分钟可以把满水池的水放尽. 一次，工作人员疏忽，打开甲、乙水管若干分钟后才匆忙关闭乙水管，又过了相同的时间才注满水池，造成了浪费. 问：甲水管一共注水多少时间？

（3）（每日一题）整理一批图书，5个人合作需要8小时. 现安排a个人先做4小时，然后增加2个人与他们一起再做8小时，这时完成的总工作量为__________. （用含有a的代数式表示）

设计说明  归纳总结课堂所学，并及时检测，了解学生课堂掌握情况，同时对教师的课堂教学效率进行及时反馈，以便在后续的教学中进行必要的调整，真正实现“趣动数学”课堂所倡导的交流生动、思维灵动、学习主动的生本课堂.

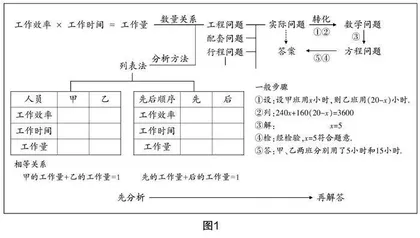
附：板书设计如图1所示.

设计说明  信息化时代，多媒体课件在课堂中运用广泛，这为我们的教学带来了很多便利. 精美的课件可以吸引学生的注意力，激发学生的学习兴趣，还能提高课堂效率，增加课堂容量. 但是，必要的板书也不可或缺. 在本课教学中，随着课堂的深入，知识框架渐次生成，并且教师根据学生的回答及时调整教学过程，以暴露学生的思维过程. 本课的板书分为三大块，上半部分，让学生感知实际问题与一元一次方程之间的联系，渗透建模思想;右下部分，是解应用题的基本步骤，这是解应用题的基础;左下部分，则是本节课的重点和难点，是解决工程问题的分析方法，教学时要突出两张分析表格. 所有的问题，都可以利用这两张表格来进行分析，不过，根据不同的题目，需要修改表格中的数据或式子，所以这两张表格是本节课的灵魂. 这样的板书设计，能形成视觉冲击，能加深学生的印象，能帮助学生在大脑中建构出知识网络.

写在最后

“趣动数学”课堂的教学模式，我们还在不断地完善，我们希望在这个模式的引领下，学生在课堂中能够“动手实践，动脑思考，动情体验”[1]，真正投入课堂，成为课堂的主人.

参考文献：

[1]茅雅琳. 基于问题链的“趣动数学课堂”教学设计及思考[J]. 数学教学通讯，2020（32）：5-7.

基金项目：江苏省教育科学“十三五”规划初中专项立项课题（E-c/2020/16）“生本理念下的初中‘趣动数学’课堂实践研究”.

作者简介：茅雅琳（1971—），教育硕士，中学高级教师，南通市数学学科带头人，南通大学特聘校外导师，多次获全国录像课评比一等奖，获省“领航杯”教学能手大赛，省“杏坛杯”苏派青年教师课堂教学展评一等奖.