激发初中生数学学习动机的课堂教学策略研究

［摘  要］ 学习动机作为非智力因素中的一种，可以有效唤起学生的学习动力. 文章试从学生学习数学的角度，阐释激发学习动机的有效策略：以“问题”启动“欲望”，触发学习动机；以“难度”确定“程度”，维稳动机水平；以“反馈”促进“深化”，深化学习动机.

［关键词］ 学习动机；问题；激发；初中生

对学生而言，任何一门学科的学习都应是一种有意识的活动，需要借助激励来推动学习的内部动力，以达到高效学习的目的，这种内部动力就是学习动机. 可见，学习动机作为非智力因素中的一种，可以有效唤起学生的学习动力，所以在众多非智力因素中一直处于关键性地位，引起了国内外专家、学者的全面关注，且国内外专家、学者针对性地提出了一些理论方法. 但是，当前一些教师仍然十分重视知识的传授，强调知识本位，却忽视了学生学习动力的激发与培养. 本文试从学生学习数学的角度，阐释激发学生学习动机的有效策略.

以“问题”启动“欲望”，触发学习动机

内部动力是兴趣的根基，兴趣是内部动力的外化，兴趣越浓厚，内部动力就越强烈. 一个人一旦有兴趣，就会激起探究欲望，并通过动手、动脑、动口来满足自身的欲望. 因此，教师要在教学中创设独特的问题情境，引发学生的好奇心与探究欲，使其产生了解这个概念、公式、规律的迫切心理，进而触发学习动机. 在强烈的学习动机指引下，学生的思考与探究往往更加深入. 反之，如果学生没有产生学习动机，随意地听讲或学习，往往会陷入效率低下的糟糕境地. 当然，教师在通过各种情境创设触发学生学习动机之时，要善于引导、点拨和激励，使深入探究成为学生兴趣的持久支撑力.

案例1 以“平方差公式”的教学为例.

师：我先来给你们讲一个故事，好不好？（学生瞬间变得兴趣盎然）

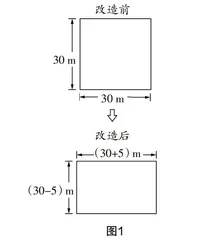
师：听完故事之后，要回答问题哟！这是一个庄园主与租户的故事. 一个狡猾的庄园主长期租赁一块边长为30 m的正方形土地给刘老汉. 有一天，他通知刘老汉，他要改造土地，将租赁给刘老汉的那块地的一边减少5 m，邻边增加5 m，变成一块长方形土地，仍然以相同的租金租赁给刘老汉，并说反正刘老汉没有吃亏. 刘老汉听了庄园主的话，思考了片刻，认为自己的确没有吃亏，便一口答应了. 回家后，刘老汉将当天发生的事情告诉了夫人，聪明的夫人一口断定刘老汉吃亏了. 你们认为刘老汉有没有吃亏？请说出理由.

（听完故事，学生各个跃跃欲试，有的计算，有的画图，有的讨论）

生1：如图1所示，原来土地的面积为302 m2，改造后土地的面积变为（302-25）m2.

师：看来刘老汉的夫人说对了，刘老汉真的吃亏了，吃亏了25 m2.

师：在刚才的探究中，你们可有其他发现？

生2：根据302-25=（30+5）（30-5），我猜想两个数的和与这两个数的差的乘积等于这两个数的平方差.

师：非常好. 今天这节课就让我们一起来证明生2的猜想，并利用这个公式去解决一些相关的数学问题.（教师板书课题）

学生只有具备学习动机的心向，才能让深度学习真正发生，才能让高效课堂的构建成为可能. 在“案例1”中，教师巧妙地从学生喜闻乐见的故事入手，在故事情境激趣的情形下，使他们产生积极的学习动机，使数学的深度探究水到渠成.

以“难度”确定“程度”，维稳动机水平

让学生产生积极的学习心向对数学学习来说十分重要，与此同时，维稳动机水平更重要. 因此，教师要根据教学内容的难易度来把控好激发学习动机的程度，以促进课堂教学高效推进.

当教学内容容易被学生接受时，教师要有目的地集中学生的注意力，通过适度施加压力来提升学生的紧张感，从而为后面知识点的快速抛出和吸收做好准备. 例如，负数知识较为基础，也十分重要，在课堂导入时，教师可以这样引导：“各位同学，今天我们所学内容的掌握程度直接影响着后面其他知识的学习，我们不能小看这些看似简单的知识. 事实上，这部分知识需要掌握的内容非常丰富，如负数的含义、负数的运算等，尤其是运算中的易错点，需要我们集中注意力，在老师的思路引领下一一突破. ”就这样，教师化压力为动力，很好地提升了学生的学习动机，从而为后面学生的高效学习做导引.

当教学内容为教学难点时，教师要有意识地创设轻松、自由、和谐的教学氛围. 例如，“一次函数”十分重要，却不易掌握，这就需要教师做好课堂气氛的调节，让学生在无负担、无焦虑、有信心的情况下进入深度学习状态. 在学习的过程中，当有些函数问题学生掌握得不够好时，教师还应进行如下引导：“在今天的学习中，你们只需要弄懂一次函数的含义、数值代表的意义，有些难点问题，如y=x+1中的“1”表示的是直线与y轴交于y轴的正半轴；y=x-1中的“-1”表示的是直线与y轴交于y轴的负半轴. 这些知识都比较抽象，如果无法理解，可以在后期的学习中慢慢摸索、砥砺前行.”

教师正确处理各种情况，激发学生的学习动机，做好学习动机的维稳工程，能让学生在学习中真正地做到细心、乐观、快乐，从而让更多的学生乐于沉浸在数学世界中.

以“反馈”促进“深化”，深化学习动机

教师要关注课堂教学过程中的即时反馈，要注重对探究活动和课堂练习等情况进行合理评价，从而有效地融合反馈与评价，发挥好信息反馈的诊断、导向和激励功能，最终在学习动机不断深化后，让学生依然充满学习动力，并富有个性地进行数学学习.

案例2 用一元一次方程解决实际问题.

问题情境：一上市公司长期销售甲、乙、丙三种产品. 在去年全年的销售中，高新产品丙的销售额占销售总金额的40%. 受疫情的影响，今年甲、乙两种产品的销售额均会比去年减少20%，鉴于高新产品丙是今年的销售重点，该公司想让今年的总销售额与去年相当，那么今年产品丙的销售额需比去年增加多少？

下面是学生小组的展示实录.

生1：本题并没有出现销售总金额，因此我们可以设去年的销售总金额为“1”，今年产品丙的销售金额需比去年增加x，于是可以得到方程40%（1+x）+（1-40%）（1-20%）=1，解得x=0.3=30%.

生2：我觉得这里需要解释一下这个等量关系的含义. 40%为产品丙去年的销售额，40%（1+x）就是产品丙今年的销售额，（1-40%）是产品甲和乙去年的销售额之和，（1-40%）（1-20%）就是产品甲和乙今年的销售额之和. 因为今年的销售额与去年相当，所以40%（1+x）+（1-40%）（1-20%）=1.

生3：我觉得能列出这个方程，关键在于通过去年产品丙的销售额来表示今年产品丙的销售额，通过去年甲和乙这两种产品的销售额之和来表示今年甲和乙这两种产品的销售额之和.

生4：我有不同的思路. 可以这样想，既然今年的总销售额与去年相当，可见产品丙增加的销售额等于产品甲和乙减少的销售额之和，于是可得方程40%x=（1-40%）×20%，解得x=0.3=30%.

师：哇，老师都没想到还有如此简便的思路！生4的思路真是既简便，又富有创造性. 看来生4不仅在课堂中进行了深入的思考，课前也做了预习工作，所以才能在课堂中发散思维. 真不错！其他人明白生4的思路了吗？下面，请每个学习小组再次梳理这一解题思路，并回忆一下通过本课的学习你收获了什么，还有什么疑惑需要向别人请教.

……

学习效能的提升有赖于教学环节的设计，环节中学生学习动机的延伸更是教学成败的关键. 为了让课堂教学更有深度，让学生的思维更加灵动，教师可以即时反馈学生的学习情况，让学生看到自身的进步和思维的闪光点，同时认识到自身的错误，并及时修正. 可见，实施激励性措施，能让学生挖掘学习中利于自身发展的因素，从而扩大自身进步的空间，最终学会学习，学会思维管理.

总之，在学习动机的驱使下，让学生在兴趣和好奇中直达数学问题，掌握数学本质，这就是数学教学的目的. 学习动机的激发能让学生思维能力的培养事半功倍，且学习动机的激发与数学知识的学习相辅相成. 要全方位地激发学生的学习动机，需要有效问题的提出，需要维稳工作的支持，还需要即时反馈，这样才能让学生在宽松的环境、愉悦的情绪中获得新知，形成智慧，发展能力.