“课程思政”视域下的高中数学教学探索与实践

［摘  要］ 高中数学教学可以数学文化为载体，渗透“课程思政”元素，发挥其育人价值.研究者以“函数概念的发展历程”为例，探析“课程思政”视域下的高中数学教学实践，实现知识传授、素养提升和价值引领和谐统一.

［关键词］ 课程思政；数学文化；函数概念

提出问题

课程思政是指以构建全员、全程、全课程育人格局的形式将各类课程与思想政治理论课同向同行，形成协同效应，把立德树人作为教育的根本任务的一种综合教育理念［1］. “课程思政”理念体现了中国对学科德育的特色化改造，将课程思政与学科教学融合，正是实现立德树人目标的有效途径. 高中数学作为高中阶段的核心学科之一，能否精准定位知识内容的切入点，融入课程思政元素，以发挥数学学科的育人功能呢？课程思政在数学学科中的一个重要体现就是数学文化. 数学文化是指数学的思想、精神、方法、语言、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动［2］10. 《普通高中数学课程标准（2017年版2020年修订）》在“教学建议”中提到：“在教学活动中，教师应有意识地结合相应的教学内容，将数学文化渗透在日常教学中，引导学生了解数学的发展历程，认识数学在科学技术、社会发展中的作用，感悟数学的价值，提升学生的科学精神、应用意识和人文素养；将数学文化融入教学，有利于激发学生的数学学习兴趣，有利于学生进一步理解数学，有利于开拓学生视野、提升数学学科核心素养.”［2］82将数学文化融入数学教学，可以揭示知识的发生和发展过程，丰富学生的情感体验，充分发挥数学课程的德育价值，为课程思政的实施提供有效路径．

数学文化中的思政元素

广义的数学文化包括数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等［3］. 接下来，谈谈如何从数学文化中挖掘高中数学课程思政的元素.

1. 科学价值

当概念以历史的脉络展现时，它揭示了知识发展的自然与和谐，为数学注入了鲜活的生命力，并为学生打开了学习数学的新视角. 通过这种方式，学生能够更深入地理解数学概念、数学思想以及历史背景. 当方法以历史的视角呈现时，它揭示了表征方式、数学语言和计算方法的演变，通过古今数学方法的对比，学生能进一步认识到个体对数学的理解过程遵循数学历史发展轨迹，学会以辩证的视角看待问题. 当思想以历史的维度展开时，它揭示了历史背景下数学思想的发展和变迁，使学生感受到数学与现实生活之间的紧密联系，从而获得深刻的数学体验. 当知识理解的过程以历史的线索呈现时，它揭示了我们认识事物的一般规律，从直观到抽象，从模糊到严谨，从简单到深入，逐步完善，这与学生学习数学知识的过程具有相似性，体现了科学的价值. 当数学语言以历史的进程展现时，它揭示了从感性到理性，从烦琐到简洁，从粗略到精确的转变，这一过程也是学生学习数学的必经之路. 因此，数学文化中的数学史对于培养学生的学习兴趣、哲学思考和理性思维具有重要的科学价值.

2. 人文价值

数学文化凸显了数学的人文情怀，让学生认识到数学远不止于冰冷的公式和符号，它背后蕴含着众多数学家的深思与探索历程；让学生感受到前人对科学的不懈追求和执着精神，激发他们对科学的持续探索和学习的热忱；让学生体会到数学家的创新思维，敢于质疑，勇于挑战，不断推进数学的进步；增强学生的民族自豪感和文化自信，培养他们的社会责任感，强化爱国教育. 通过数学家的故事，学生不仅了解到“伟人”的生平与成就，更重要的是汲取了榜样的力量，锻炼了坚强的意志，学习了严谨的数学治学精神. 每一个数学家都是一部数学史，每一个数学概念的诞生往往是众多数学家前仆后继、不懈努力的成果. 学生通过阅读数学家的生平故事，产生共鸣，更深刻地理解学习过程中的苦与乐，学会像数学家一样思考问题，在这一过程中更加明确学习的目标和方向.这正是数学家所体现的人文价值.

3. 品质培养

通过深入阅读和思考数学文化，学生将逐渐培养数学阅读的技巧，并提升深度探究的能力. 在阅读初期阶段，学生需要理解文化背景，提取数学信息，并领会符号的深层含义. 例如，在探索函数概念的发展历程时，学生会遇到众多数学专业术语，如狄利克雷函数、傅里叶级数、微积分等，一方面考验学生的学习耐心，另一方面激发学生的学习欲望. 在阅读中期阶段，学生应致力于理解数学概念，吸收数学史料，并体验数学思想. 例如，在函数概念的教学中，学生常有疑问：既然初中已经学过函数概念，为何高中还要以另外的方式重新学习呢？要深刻解答这个问题，就要回归函数概念的发展史，才能让学生真正理解概念的演变和思想的深化. 在阅读末期阶段，学生要整理数学知识，应用数学知识，解决实际问题. 这一过程是学生在阅读中学会自我学习和自主探究的关键阶段. 通过阅读和思考数学文化，学生能够将这些技能迁移到日常学习中，逐渐培养出良好的阅读习惯和自学能力，从而提升数学学科核心素养.

案例呈现

本文以高中数学必修第一册（人教A版）中的“阅读与思考”栏目——“函数概念的发展历程”为例，探析“课程思政”视域下的高中数学教学实践.

1. 前置阅读任务

在课前阅读课本中的材料“函数概念的发展历程”，并搜集相关的历史资料；在搜集资料的过程中，思考以下问题：

（1）函数概念产生的背景是什么？

（2）函数概念的发展历程是怎样的？

（3）从数学史的角度来看，初中和高中对函数概念的定义有何区别？

（4）中文中的“函数”一词是如何引入的？

思政育人 培养乐学善学的态度、锻炼理性思维、养成良好的学习习惯，使学生能够轻松解读课本的阅读材料，梳理函数发展的脉络，在阅读中进行思考，在思考中深化阅读.

2. 师生活动，展示交流

通过资源整合与相互交流，学生初步重构并梳理函数概念发展历史，明确函数概念发展的五个阶段. 在小组讨论中分配任务，由代表阐述某位数学家在函数概念发展历程中的贡献，其他小组成员则可适时进行补充.

活动1 阐述函数发展的背景

通过阅读材料，发现运动的研究问题都需要探究两个变量之间的关系，这是函数概念产生与发展的背景. 引导学生深入思考：17世纪，科学家为何要计算天体的位置？为何要在远洋航海中测量经度和维度？为何要计算炮弹的射程？等等. 通过这些问题，让学生从历史的角度探索数学概念的起源，从而理解数学如何成为推动社会进步的重要工具.

活动2 理清函数发展的阶段

通过整合交流的资料，学生简明扼要地重构函数概念的发展历程，明确函数概念发展的五个阶段：几何起源—解析式说—变量依赖说—对应说—关系说.

思政育人 培养社会责任感、倡导乐学善学、锻炼理性思维，让学生深刻理解数学概念的形成不仅源于数学内部，还与社会进步和生产需求紧密相关；通过学生之间的互动交流，引导他们透过表象洞察本质，进行理性分析，学会独立思考，从而树立正确的数学观念.

活动3 梳理函数概念发展的历程

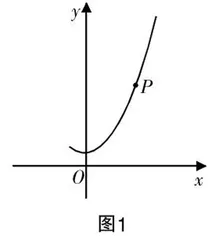
思考1 如图1所示，在平面直角坐标系中，曲线C上的任意一点P运动时，你能找出哪些几何量会随之发生变化呢？

学生很容易想到点P与x轴、y轴、原点的距离都会发生变化，∠xOP也会改变. 如果过点P作一条切线，使其与x轴相交于一点，那么点P与这个交点的距离同样会发生变化. 这些几何量的变化与函数有什么关系呢？这正是探讨函数概念的几何起源的出发点.

学生展示（见表1）：

师生互动：

生1：原来函数的概念源于几何学，它描述了随着点的横坐标变化而变化的几何量. 看来，学习函数图象很重要.

师：是的，几何学的起源不仅孕育了函数图象的初步形态，而且后续学习的许多数学定义都源于对几何图形的抽象概括. 数形结合思想是我们理解数学概念的关键工具.

生2：那么，如何刻画变量之间的关系呢？

师：这是个好问题. 历史上，数学家们在攻克微积分难题时也遇到过这一问题，他们是如何解决的呢？

学生展示（见表2）：

师生互动：

生3：数学家们通过解析式刻画了两个变量之间的关系.

师：函数从几何图形的理解到代数式的表达，你有什么看法呢？

生4：解析式能更精确地描述两个变量之间的关系.

生5：所有的函数都有解析式吗？所有的函数都有图象吗？

师：大家的想法特别棒，提出的问题也是历史上困惑数学家们的问题.

思考2 18世纪中期，数学家们一直争论着一个关于振动弦的问题：拨动一根两端固定的弹性弦，使其形成某种初始形状后释放，它将开始振动. 那么，如何用函数来描述某一时刻弦的形状呢？

生6：如果把弦的振动看成一段音乐的话，可以用简谱描述声音的变化.

生7：声音是连续的，可以用弦离开平衡位置的位移来描述弦的振动状态，但时间与位移之间的解析式怎么写呢？

师：当弦振动时，数学家们对任意一段曲线是否有函数解析式展开了讨论，从而推进了函数概念的发展.

学生展示（见表3）：

师生互动：

生8：也就是说，函数不必非得用解析式来表达；只要两个变量之间存在依赖关系，那就是函数.

师：是的，欧拉和柯西对函数的定义朴素地揭示了函数概念中的辩证思想，展示了从自变量到因变量的演变过程，从而使得函数的“变量依赖”定义登上了历史舞台.

思考3 1829年，德国数学家狄利克雷为傅里叶级数引入了一个新的函数：f（x）=1，x为有理数，0，x为无理数.这个函数用“变量依赖”如何解释呢？

生9：这个函数不能用“变量依赖”解释，也不能画出它的图象.

师：能否用我们在高中所学的函数定义来解释这个问题呢？

生10：可以. 有两个集合，分别是A=R，B=｛1，0｝.集合A中的任意一个元素在集合B中都有唯一一个确定的元素与之对应. 因此，这是从集合A到集合B的函数.

师：狄利克雷圆满解释了他所创造的函数.

学生展示（见表4）：

师生互动：

师：从变量对应到集合对应，函数对应摆脱了变量的限制，将函数概念置于集合映射这一更加宽泛的框架之中，更清晰地阐释了函数的内涵，适用范围也更加广泛.

生11：原来“对应说”经历了变量对应和集合对应，集合对应就是我们高中所学习的吧.

生12：从狄利克雷创造函数到他对这个函数的解释，我深感他具有非凡的创造力.

师：是的，历史上许多数学家都是我们学习的楷模，他们的数学成就无一不是通过千辛万苦获得的. 我们应当汲取这些榜样的力量，锤炼出坚强的意志，并向数学家们致敬.

学生展示：

1939年，法国布尔巴基学派提出了一个非常形式化和抽象化的函数定义：设A与B是给定的数集，f是笛卡尔乘积集A×B=｛（x，y）x∈A，y∈B｝的一个子集（也称A与B的一个关系），如果对于任意x∈A，存在唯一y∈B，使得（x，y）∈f（等价于若（x，y），（x，z）∈f，则必有y=z），则称f是定义在A上，取值在B中的函数. 该定义基于集合论，消除了变量对应这个用语，是完全数学化的定义.该定义被称为“关系说”［4］7.■

师：至此，数学家对函数概念的探讨并未画上句号. “函数空间”“泛函”“广义函数概念”以及“超广义函数概念”仍在不断地丰富和涌现. 随着研究的深入，函数概念持续地被严谨化和精确化.