在丰富的具身体验中发展学生的直观想象素养

［摘  要］ 直观想象素养是数学学科核心素养的重要组成部分，直观想象素养对激发学生数学学习兴趣、提高学生数学能力等发挥着重要作用. 立体几何是培养学生直观想象素养的重要载体，教学中教师要重视引导学生运用直观感知、操作确认、思辨论证等方法领悟空间观念与图形性质，培养学生利用图形和空间观念分析和解决问题的能力. 同时，教师要从教学实际出发，为学生量身定制符合认知水平的探究活动，引导学生多感官参与实践活动，在丰富的具身体验中发展空间想象能力，切实将培养学生直观想象素养落到实处.

［关键词］ 直观想象素养；立体几何；具身体验

在新课程新课标背景下，培养学生数学学科核心素养已成为高中数学教学的重要课题. 直观想象素养是指通过观察、想象、猜测等方法来探究数学问题，并利用图形等直观方式来解决问题. 培养学生直观想象素养对培养学生思维能力和问题解决能力具有重要意义. 在发展学生直观想象素养的过程中，不仅要加强基础知识教学，还要注重实践教学，既要让学生动脑想，又要让学生动手做、动口说，从而让学生通过多感官的共同参与获取数学知识抽象内容的本质，发展几何直观和空间想象能力，培养直观想象素养. 在具体实施过程中，教师要结合教学实际设计一些有价值的探究活动，为学生营造一个和谐的学习氛围，充分发挥学生的主体价值，重视调动多种感官参与教学活动，通过具身体验更好地理解数学知识，提高空间想象和解决问题的能力. 笔者以“直线与平面平行”的教学为例，谈谈发展学生直观想象素养的一点拙见，若有不足，请指正.

教学分析

1. 教材分析

“立体几何”是“空间与图形”课程的延续与发展，学生借助空间认识物体的大小、形状和位置关系，通过调动眼、手、脑等多种感官认识空间图形的结构和性质，逐渐形成直观想象素养. 在学习线面位置关系之前，学生学过线线位置关系，其相关知识和经验为本课学习打下了基础. 而本课内容也是后续学习面面位置关系的基础，可见本课内容从知识结构上起到了承上启下的作用.

2. 学情分析

从知识层面来看，学生学过空间几何体，对直线与直线、直线与平面、平面与平面的位置关系有一定的认识，加上学生掌握了研究空间直线与直线位置关系的方法，这为自主探究活动的开展创造了条件. 从能力层面来看，高中生具有一定的空间想象、逻辑推理、数学抽象等能力和素养，因此教学中教师要相信学生，鼓励学生自主探究，以此培养学生的自学能力. 不过大多数学生空间想象能力相对较弱，缺乏从空间转化为平面的思维，语言表达能力也相对不足，学生在学习过程中可能会遇到一些障碍，对此教师要适时启发和指导，通过师生有效合作，构建生态课堂.

3. 教学目标

（1）在丰富的具体体验中理解并掌握线面平行的判定定理，发展学生的空间想象能力；

（2）通过对判定定理的论证，培养学生的理性思维和严谨的学习态度；

（3）通过引导学生主动参与、积极探究的过程，激发学生数学学习的主体性、主动性和积极性意识，发展学生的几何直觉思维，培养学生的直观想象素养.

4. 教学重点和难点

（1）理解并掌握线面平行的判定定理和性质定理；

（2）空间观念的发展和逻辑思维能力的培养.

教学设计

1. 领悟线面平行的定义，培养学生的空间观念

数学范畴的定义法是指用数学定义解决问题的一种方法，是一种常见的解题策略，也是一种基本素养. 应用定义法的前提是熟练掌握相关定义，对于同类概念要十分清晰它们之间的共性和细微差异，以此有效避免因错用而引发错误. 利用线面平行的定义来研究线线、面面之间的关系，有利于学生加深对线面平行的理解，拓宽学习视野，增强思辨能力，发展直观想象素养.

问题1 已知直线CD在平面α内，若直线AB平行于平面α，则直线CD与AB存在怎样的位置关系？

问题给出后，教师预留时间让学生操作、观察，直观感知直线CD与AB之间的位置关系，从而为研究线面平行的判定定理埋下伏笔.

问题2 在同一平面内，过直线外一点作该直线的平行线，我们可能得到几条符合条件的平行线？如果将其迁移到空间里，你有什么发现？

在教学中，从学生已有的平面几何学习经验出发，引导学生建立平面与空间的联系. 这样通过类比，引导学生发现并提出问题，激发学生学习的积极性，增强学生的空间思辨能力. 同时，通过渗透类比的研究方法，有利于提升学生的转化意识和问题意识，促成深度学习.

问题3 已知AB∥CD，且AB平行于平面α，则CD与平面α存在怎样的位置关系？

该问题较为抽象，对于初学立体几何的高一学生来讲，具有一定的难度. 为了突破这一难点，教师可以借助实物进行展示，充分发挥几何直观的优势，培养学生运用图形来研究数学问题的意识，提升学生直观想象素养. 同时，通过实物展示、操作确认，可为学生积累丰富的感性素材，从而为后续学习线面平行、面面平行的判定定理提供依据.

上述三个问题让学生从不同角度领悟线面平行的定义，从而为接下来研究线面、面面平行做好知识、方法及技能的准备，发展空间观念.

2. 直观感知线面平行判定定理，提升直观想象素养

众所周知，几何平面可以看成由无限条直线组成，直线可以无限延伸，则平面自然也可以无限延伸. 由于两者具有无限延伸性的特征，因此用定义来判定线面平行是难以操作的. 基于此，教学中不妨从生活实例出发，让学生借助生活中的实例来感受线面平行的位置关系，从而化抽象为具体，让学生感受数学与生活的密切联系，激发学生的学习热情，提升学生的直观想象素养.

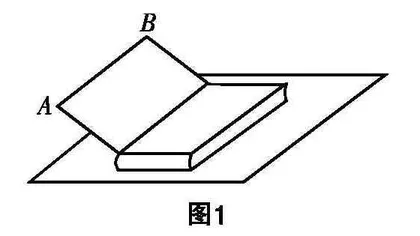
活动1 如图1所示，桌面上放置一本翻开的书，试分析封面边缘所在直线AB与桌面具有怎样的位置关系.

活动2 为了加强体育锻炼，某校买了一批单杠，安装时要确保单杠与地面平行，如果让你设计安装方案，你想怎么做？

以上两个活动给出后，教师先让学生独立思考，然后进行组内交流，接下来展示交流成果，并让学生归纳问题解决所涉及的数学思想方法，以此让学生更深层次理解知识.

在教学中，以生活为背景，让学生直观感知线面平行的位置关系，有利于发展学生的直观想象素养. 在活动中，教师预留充足的时间让学生动手做、用眼看，并主动交流自己的所思、所想，以此通过具身体验积累丰富的几何直观经验，发展空间观念. 在此过程中，教师引导学生学会用数学的眼光分析和解决现实问题，用数学的语言去表达现实世界，有利于锻炼学生的语言表达能力，提高学生的数学抽象素养. 这样通过积极参与，学生对直线与平面平行的判定有了初步的认识，此时教师给出线面平行的判定定理自然水到渠成了.

在教学中，教师从学生的认知水平出发，以生活为依托，引导学生观察生活模型、提炼空间图形、概括判定方法，从而通过多感官的参与，加深学生对知识的理解，发展学生的空间观察能力，提升学生的直观想象素养.

3. 推理论证线面平行的性质定理，培养严谨思维能力

问题4 已知直线AB平行于平面α，那么在平面α内，是否存在与直线AB平行的直线？若存在，请说说它们具有怎样的特征；若不存在，请说出你的理由.

在教学中，教师提供时间让学生互动交流，鼓励学生动手操作获得直观感知，并利用已有知识进行推理验证，以此培养思维的严谨性. 在此基础上，教师还可以引导学生将线面平行的性质定理和判定定理进行对比分析，以此让学生体会类比、转化等数学思想方法的魅力，感悟线线平行与线面平行的区别与联系，帮助学生积累丰富的证明经验，优化学生的知识结构，提升学生的直观想象素养.

4. 课堂交流与反思，全面提升数学素养

问题5 通过本课的学习，请从知识、技能、思想方法等角度谈谈你的收获.

课堂小结在课堂教学中是必不可少的，小结时教师切勿越俎代庖，要提供时间和空间让学生反思回顾，明晰本节课的知识结构，领悟数学思想方法，逐步完善知识框架图，构建完善的知识体系. 同时，通过反思归纳，培养学生良好的反思习惯，使学生在知识、能力、情感三个维度得到提升，促进学生的数学学科核心素养全面落实.

教学思考

1. 从知识层面看本课教学

本课教学共分四个环节：环节1以问题为导向，让学生通过直观感知和思辨论证体验线面平行定义的抽象过程，全面深刻地理解定义. 环节2和环节3以现实生活为依托，让学生主动构建空间图形，通过经历线面平行的判定定理和性质定理的抽象过程，领悟“几何的思维”方式，掌握研究途径与方法. 另外，在教学中，教师有意识地引导学生进行对比分析，以此加深学生对知识的理解，培养学生的转化意识. 环节4以反思、归纳本课内容为主，让学生更好地认识知识、提炼方法、升华认知，逐步建构完善的知识体系，为知识的应用打下坚实的基础.

2. 从素养层面看本课教学

在立体几何教学中，教师不单要让学生掌握知识，还要关注学生直观想象素养的培养. 培养学生的直观想象素养是一个慢过程，它无法依赖讲授来完成，而是需要学生自己去观察、去操作、去感悟. 因此，在实际教学中，教师要运用观察、操作、猜想、论断等手段展开立体几何教学，以此培养学生的空间观念，激发学生的潜能，提升学生的数学素养. 在培养学生直观想象素养的过程中，教师应关注以下几点.

（1）注重提升自身素养.

教师是课堂教学的组织者、引导者、点拨者和启发者，教师的教学观念、数学能力、数学理解等直接影响着教学效果. 若想上好课，则教师要认真研究数学、研究教学，不断更新教学手段和教学方式，注重提升自身素养. 在具体实施过程中，教师要从教学实际出发，精心设计教学活动，充分调动学生参与课堂的积极性，从而让学生由被动学习变成主动思考，提高课堂教学的有效性. 例如，在本课教学中，提高学生的几何直观能力和发展学生的空间观念是本课教学的重要目标之一. 为了这一教学目标的落实，教师精心设计探究活动让学生自主探究与合作交流，充分调动学生参与课堂的积极性，让学生在观察、操作、交流中深化对知识的理解，发展学生的空间观念和直观能力.

（2）关注学生的主体价值.

在教学中，教师不仅要关注“教”，还要关注“学”，要站在学生的视角提出问题，并鼓励学生大胆地说出自己的想法，以此提高学生的参与度，构建“以生为主”的生态课堂. 立体几何相关知识是比较抽象的，对学生的空间思维能力的要求较高，若想让学生真正理解知识，教学中必须重视学生的思考，凸显学生的主体地位，引导学生主动参与数学概念、定理等内容形成的过程，让学生主动获取知识，提升数学学习能力. 例如，在本课教学中，教师没有直接将知识灌输给学生，而是从学生实际学情出发，量身设计符合学生认识水平的问题，引导学生经历探索线面平行的定义、判定定理和性质定理的全过程，充分体现学生的价值，促进学生空间想象能力的发展和直观想象素养的提升.

（3）重视具身体验的价值.

数学知识是比较抽象的，为了让学生更好地理解知识，教师应带领学生走进生活，让学生在生活中寻找数学，充分调动学生的具身体验，通过多感官通道帮助学生厘清问题的来龙去脉，促进学生深化理解知识，提升数学能力. 例如，在本课教学中，教师不仅让学生动脑，还鼓励学生动手、动嘴，通过多感官的参与让学生理解并掌握立体几何问题的研究路径和方法，逐步提高其综合能力与综合素养.

总之，培养学生的直观想象素养是一个长期且复杂的过程. 在日常教学中，教师应重视引导学生参与知识形成的过程，培养学生理性的思维习惯，提高学生发现、分析和解决问题的能力，提升学生的数学学科核心素养.