素养导向下的单元整体教学设计

［摘  要］ 单元教学是落实学科核心素养、实现学科育人的基础和重要路径. 文章以数学学科核心素养为导向，以“三角公式”为例，通过问题串引导教学，将碎片化学习转变为结构化学习，确保核心素养在课堂中得到实施.

［关键词］ 核心素养；单元整体教学；三角公式

引言

《普通高中数学课程标准（2017年版2020年修订）》（下文简称新课标）强调高中数学课程以学生发展为本，落实立德树人根本任务，培育科学精神和创新意识，提升数学学科核心素养［1］10. 本文提出按主线设置课程体系，将知识整体化、结构化，促使课程教学设计从关注单个知识点转向关注单元整体设计［2］. 在学生已有知识和发展水平上，将数学知识分成不同的单元，搭建起一个由单元大主题统领，各子主题相互关联，逻辑清晰的教学单元，促进学生建构知识框架和认知框架［3］.

本文重新整合三角函数知识，以数学学科核心素养为导向，从单元整体教学视角探讨“三角公式”的教学.

“三角公式”单元整体教学设计

1. 单元主题生成

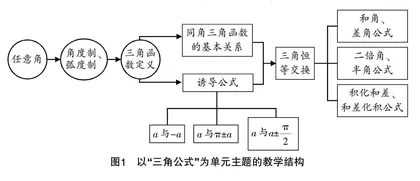
“三角函数”是人教A版（2019）高中数学必修第一册教材第五章的内容. 本章内容包括“三角函数的图象与性质”和“三角公式”两大模块，现抽取“三角公式”作为教学主题，引导学生基于三角函数定义推导三角公式，理解同角三角函数、诱导公式和三角恒等变换的关联. 根据教学内容建立以“三角公式”为单元主题的教学结构，如图1所示.

2. 单元教学内容分析

三角公式是三角函数的重要部分，从三角函数这章的内部结构来看，三角公式的产生和发展遵循一定的逻辑顺序.

首先，基于学生对角的认识和理解，结合日常周期性现象构建模型，产生认知冲突，从而引入任意角的概念；为了统一单位，引入弧度制；结合数学模型，以单位圆为工具获得三角函数的定义，发现同角三角函数的基本关系.

其次，引导学生发现当两个角的终边相同或在特殊位置时，对应的三角函数值之间的关系，推导出诱导公式.

最后，探讨任意两角的和（或差）的函数值及二倍角、半角公式.深入剖析知识间的联系，厘清知识间的脉络，以问题串的形式层层递进，激发学生的探究欲，促进数学核心素养的发展.

3. 单元整体教学过程

（1）情境创设

核心素养的培养落实在发现问题、思考问题、解决问题的过程中，通过合理的设置引导学生学会用数学思维思考问题，是落实核心素养的保障［4］. 本单元的教学情境设置可做如下考虑.

情境1 如图2所示，单摆从某时开始每秒来回摆动一次，如何刻画单摆离开平衡位置O的位移s（单位：m）与时间t（单位：s）的关系？

情境2 如图3所示，设筒车上每一个水桶都做匀速圆周运动，每6分钟转一圈，如何刻画水桶距离水面的相对高度h（单位：m）与时间t（单位：s）的关系？

思考 这两个现象有什么共同特征？

设计意图 上述两个情境不能用熟知的函数模型刻画，从而引发学生认知冲突，让学生体会学习新函数的必要性.

（2）模型建构

如图4所示，设筒车做匀速圆周运动，中心为O，转轮半径为10 m，每6分钟转一圈，水桶为点P，从初始位置A（OA与水面平行）开始逆时针转动.

问题1 一段时间后，如何计算水桶转动的圈数？此时点P距离水面的高度是多少？

为方便计算，把10 m记为1（单位：10 m），以O为原点，水平方向为x轴，竖直方向为y轴，建立平面直角坐标系，如图5所示.

思考 ①如何刻画水桶转动的圈数？②点P的高度由几个量刻画？③h（单位：m），t（单位：s）与水桶转动的圈数有何关系？

设计意图 将实际情境抽象成数学问题，引发学生思考几个变量间的关系，可知时间t（单位：s）与水桶转动的圈数相互对应；时间可以确定高度，但高度不能确定时间.通过动态展示，引导学生发现∠AOP与时间和圈数也相互对应，以此引发学生认知冲突.

追问1：初中学习的角的范围是多少？这个范围能描述筒车旋转吗？

设计意图 随着时间变化，初中学习的角不足以描述筒车旋转，因此需要扩展角的定义，引入任意角的概念.

追问2：筒车上一点从初始位置A逆时针转动到点P（如图5所示），点P的位置由哪些量确定？

引导学生建构平面直角坐标系，发现点P的位置与圆半径、∠AOP或有关.

设计意图 将筒车转动问题抽象成数学问题，发现点P的位置可以用角度或弧度刻画，但是进制不统一，导致研究不便，需学习新知识以理解引入弧度制的必要性.

追问3：我们能否用十进制的实数来度量角的大小呢？

引入弧度制：用弧度作为单位度量角，长度等于半径长的圆弧所对的圆心角叫做1弧度的角，记为1 rad. 角度与弧度的换算：1°= rad，1 rad=

°.

设计意图 引导学生探究圆中弧长与角度的关系，并通过动态演示揭示角度与弧度的转换，从而介绍弧度制.

（3）知识探究

问题2 按照图5建立平面直角坐标系，设转轮半径为1（单位：10 m），设∠AOP=α（单位：弧度），若α取，，，点P分别处于什么位置？若α为任意角，如何刻画点P的位置？

引入几个特殊的角，发现点P的位置由其坐标确定，由此得到三角函数的概念：把点P的纵坐标y叫做α的正弦函数，即y=sinα；把点P的横坐标x叫做α的余弦函数，即x=cosα；把点P的纵坐标与横坐标的比值叫做α的正切，即=tanα（x≠0）.

设计意图 先引入几个特殊的角进行探究，让学生发现用角α可以确定点P的位置；再以动态演示的方式呈现点P的运动过程，建立点P的横、纵坐标与角α的函数关系.

问题3 当点P在单位圆上逆时针转动角α时，点P到圆心O的距离能否用三角函数值表示呢？

基于三角函数的定义，计算点P的坐标，然后应用两点间的距离公式求得OP的长度，由此得到同角三角函数的基本关系：sin2α+cos2α=1，tanα=

α≠kπ+，k∈Z

.

思考 若圆的半径为r，上述式子还成立吗？

设计意图 先引导学生思考点P到圆心O的距离（圆的半径）是否也与三角函数值有关，促使他们探究同角三角函数的基本关系；接着引导学生思考圆半径任意时同角三角函数的基本关系式是否仍然成立，让学生发现同角三角函数的基本关系式与角α有关，与圆的半径无关.

问题4 基于三角函数的概念可知，三角函数值与角的终边有关，若两个角的终边相同或处于特殊位置时，对应角的三角函数值有什么关系？

根据三角函数的定义可知，终边相同的角的同一三角函数的值相等，由此得到诱导公式一；角α的终边关于原点、x轴、y轴和y=x对称，可得角π+α，-α，π-α和-α的终边，由此得到诱导公式二～公式五；角-α的终边关于y轴对称，可得角+α的终边，由此得到诱导公式六.

设计意图 由三角函数的定义可知，三角函数的概念是用角的终边与单位圆的交点刻画的，因此在探究过程中观察终边相同或对称时，点坐标之间的关系，深化学生对三角函数的理解.

问题5 观察诱导公式发现，角α与特殊角π，的和（差）的三角函数与角α的三角函数有一定关系，那么角α与任意角β的和（差）的三角函数与角α，β的三角函数是否也有一定关系？

追问：①若角α等于角β，它们之间的关系又是怎样的呢？②和（差）角公式通过怎样的运算能得到积化和差公式？

以三角函数概念和诱导公式为基础，结合圆的对称性，利用坐标法证明和（差）角公式，再将β特殊化，推导出二倍角公式. 观察和（差）角公式的公共部分，通过相加减得到积化和差公式.

设计意图 先观察诱导公式中各特殊角与任意角α的和（差）角关系式，从而思考探究和（差）角公式；然后结合三角函数的概念，发现其本质是找到角的终边与单位圆的相交点的坐标，利用坐标法推导出两角和与差的余弦公式，进而推导出两角和与差的正弦、正切公式；最后引导学生观察和（差）角公式，推导出二倍角公式和积化和差公式.

教学感悟与反思

新课标提出：整体把握教学内容，促进数学学科核心素养连续性和阶段性发展［1］82. 鉴于此，围绕三角公式展开整体教学，有助于学生构建连贯、整合的知识结构，落实数学学科核心素养.

1. 创设主题情境，指向问题解决

数学知识与实际生活密切相关，基于此，通过围绕大主题的数学情境教学，学生能多角度分析问题，建立稳定的知识结构和价值观. 比如“三角公式”教学，通过观察筒车转动，将日常生活问题抽象为数学问题，从而引入任意角和弧度制的概念. 将实际问题数学化，再将数学问题生活化，相互贯通，潜移默化地发展学生的数学建模素养，提高学生用数学知识解决问题的能力.

2. 关注知识联系，创造解决条件

数学知识本身具有一定的逻辑性，因此，在单元整体教学视角下，要剖析大主题内各子主题间的关系，引导学生建构更加全面和完整的知识体系.比如基于三角函数的定义提出问题：当两个角的终边相同或处于特殊位置时，对应的三角函数值有什么关系？通过三角函数的定义发现三角函数值与角的终边有关，以此引发学生重点探究角的终边处于特殊位置（如关于原点对称等）时相应三角函数值之间的关系，进而为诱导公式的推导创造条件.因此，在大单元指引下，教师站在整体的高度俯瞰知识间的联系，实现重点突出、安排合理、生成自然.

3. 践行学生为本，推动素养发展

单元整体教学并非简单地把几节课内容进行叠加，而是以知识间的逻辑关系为基础进行串联，以学生的认知发展为基础，围绕一大主题进行解析，将相互关联的主题以合理的方式进行组合.比如先由初中学习的角、角度制过渡到任意角和弧度制，再以三角函数的定义为基础推导诱导公式……在“三角公式”教学中，以学生为本，建构一系列问题串，引发学生思考、探究，帮助学生有层次、系统性地围绕一个主题开展学习，为学生探索关键知识、发展数学素养奠定基础.

4. 规划单元教学，体现育人价值

单元教学有利于整体规划核心素养的发展，有利于借助大背景、大问题、大思路、大框架进行高观点统领、思想性驾驭、结构化关联，能有效规避传统的课时教学整体感不强、知识分解过度、学习碎片化、教学效益低下的现象［5］. 教师可在单元教学中帮助学生掌握知识结构，联系实际生活，促进认知发展，提升能力和素养.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］ 喻平. 学科核心素养导向的教学理论嬗变［J］. 教育发展研究，2022，40（Z2）：78-85.

［3］ 严艳. 单元整体教学中核心素养目标的落实：以“分式”单元起始课为例［J］. 中学数学教学参考，2020（20）：25-27.

［4］ 魏侹路. 单元教学设计助力发展学科核心素养：以“三角函数”为例［J］. 数学教学通讯，2021（33）：12-14+26.

［5］ 曾荣. 单元教学的整体设计与课时实施：以“圆锥曲线”单元教学为例［J］. 数学通报，2021，60（3）：33-37.