高中数学建模应立足生活

［摘  要］ 在生活基础上数学建模，可帮助学生了解模型的形成与发展，为后续灵活应用模型解决实际问题奠定基础. 文章以“指数函数的概念”教学为例，借助两个旅游景区不同年份游客人次的变化情况，引导学生亲历“初建模型—求解模型—应用模型—总结提升”等环节，培养学生的数学思维，提升学生的建模能力，为发展学生的数学学科核心素养夯实基础.

［关键词］ 数学建模；知识；生活；指数函数

数学建模素养是《普通高中数学课程标准（2017年版2020年修订）》提出的六大数学学科核心素养之一. 数学模型对学生来讲并非一件新鲜事物，作为核心素养，其在不同阶段的表现是不同的，从小学阶段的模型意识到初中阶段的模型观念再到高中阶段的数学建模，经过了一个螺旋上升的发展过程.

数学本身是非凡、多样、多彩的. 随着新课改的深入推进，数学教师应达成这一共识：不同个体学习数学的方式有所区别，学习数学知识的目的是更好地解决生活问题，数学课堂教学应想办法激活各个层次学生的思维，挖掘学生的潜能，让学生将数学知识与生活实际有机地融合起来，为发展数学学科核心素养创造条件. 在课堂中强化建模实践，不仅能拉近生活实际与数学知识的距离，还能给学生带来丰富的学习体验，让学生领悟数学知识到生活实际的可行之道［1］.

教学过程

1. 导入新课，初建模型

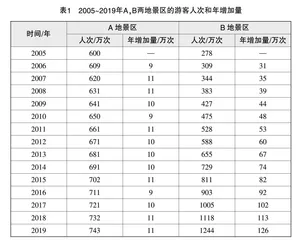
师：随着我国经济高速增长，人民生活水平不断提高，不少家庭每年都会以旅游的方式增长见识，愉悦身心，各景区游客量日益递增. 如表1所示，此为A，B两地景区2005年至2019年游客人次的变化情况. 通过对表格的观察，可发现什么规律？如何用数学知识来研究并描述这一现象？

在该生活情境的启发下，学生借助描点法将表格中的数据整理为散点图，并将各个点用光滑的曲线连接起来构成图1. 观察图形，可见A地景区的游客人次近似于直线上升，即线性增长；B地景区的游客人次则是非线性增长，各点连接而成的曲线没有明显的变化规律.

设计意图 将学生感兴趣的生活实际作为教学情境，意在引导学生感知建模过程中的理解问题与简化问题两个环节. 从理解问题的视角来看，学生从A，B两地景区游客人次的变化情况中可抽象出相应的数学问题，初步感知生活实际与数学知识的联系；从简化问题的视角来看，将表格数据简化为散点图，学生可直观洞察游客人次的变化情况，抽象出现实模型，增强数据分析能力.

2. 生成概念，求解模型

（1）大胆猜想

师：B地景区的游客人次变化情况可借助什么量来表达？

探索此问题，可进入师生活动阶段：教师先带领学生将A地景区的游客人次与时间的函数表达式（y=10x+600，x∈［0，14］，x∈N），以及当年游客人次与次年游客人次的关系（yn+1-yn=10〈等差〉，n∈N）抽象出来，再要求学生独立思考与合作交流，对B地景区各年的游客人次变化情况加以探索，猜想模型.

学生在交流过程中逐一排除一次函数、正比例函数、反比例函数，有的学生提出B地景区的游客人次的变化规律与二次函数相似，那么，这是否正确科学呢？为了探索这个问题，学生自主列式（y=ax2+bx+c，yn+1-yn=a+2an+b），同时画图分析，发现这组数据的变化规律与二次函数也不相符.

设计意图 大胆猜想，可缩小模型范围，为学生思维明确方向，也为学生从生活中提取数学模型，以及后续求解数学模型夯实基础.

（2）构建模型

师：相邻两年间的游客人次相减获得A地景区游客人次的年增长量，对于B地景区的游客人次的变化规律，能否用同种方法来分析呢？是否有其他方法？B地景区每年的游客人次增长量存在怎样的情况？

在教师指导下，学生根据2006年至2018年B地景区游客人次的变化情况建立新模型，并用新模型计算2019年B地景区的游客人次，将所得结果与已知数据进行类比，判断所构建的新模型是否准确科学.

探索发现年增长率和年增加量是该生活情境中的两个重要变化量，而B地景区无法与A地景区一样借助年增加量获得游客人次的变化规律，由此考虑用年增长率来探索B地景区当年的游客人次与上一年的游客人次的关系，即通过相除得到=a，=a，…，=a，获得模型=ax-1.

设计意图 通过数据与图象分析，学生自主进入建模状态，并在大胆猜想与思考的基础上，建构适合情境的新模型. 在此过程中，学生主动参与建模活动，感知建模步骤，体会数学知识、生活实际与建模之间的联系，建立学习自信，发展数学思维.

（3）求解模型

学生通过独立思考、自主计算与探索、合作交流，发现B地景区每年的游客人次增长率稳定在一个常数附近. 根据这个特点猜想B地景区游客人次的变化规律为=1.11x-1（x∈［1，+∞）. 至此，学生的思路变得明确.

设计意图 学生基于运算、总结与探索，提升数学运算素养与思维水平，为构建数学模型奠定基础.

3. 深化理解，完善模型

要求学生解释怎样根据数据获得相应模型，并且探索所获得的模型与现实生活是否相符.

在教师启迪下，学生以小组合作交流的方式进行思考与分析，获得如下结论：从2006年起，B地景区每年的游客人次为2005年游客人次的1.11， 1.112，1.113，…，1.11x倍. 设经过x年后B地景区的游客人次为2005年游客人次的y倍，则y=1.11x（x∈［0，+∞））. 根据模型y=1.11x（x∈［0，+∞））计算2019年B地景区的游客人次是278×1.1115-1≈1198（万次），与2019年B地景区的实际游客人次1244（万次）相比，误差为3.7%. 实践表明，模型数据与实际数据误差较小，因此确定该模型具有可靠性，可用于解决实际问题.

设计意图 此环节涉及建模过程中的“结果解释”与“修改模型”两个步骤. 基于结果解释的维度思考，即使能自主建立模型，并不表示学生已经完成了教学任务，亲历建模过程，能将模型的来龙去脉描述得清清楚楚才算是真正意义上理解了模型. 修改模型是指在实际应用模型前，检验模型与生活实际的匹配程度. 应用数形结合思想探索模型，让学生体验实际数据与模型数据的误差，认识到数学的周密性、严谨性和规范性，培养逻辑思维能力.

4. 拓展应用，发散思维

师：当生物死亡后，它机体内原有的碳14含量会按确定的比率衰减，大约每经过5730年衰减为原来的一半. 按照这种衰减规律，生物体内碳14含量与死亡年数之间有怎样的关系？

因为有了景区游客人次探索的基础，所以大部分学生都能通过独立思考构建出模型y=

（x∈［0，+∞））.

师生共同总结两函数的共性，发现函数y=1.11x和y=

都可以表示为y=ax（a>0，a≠1），其中x是自变量. 学生亲历建模过程，不仅自主获得了可以解决生活实际问题的模型，还自然而然地理解了指数函数.

设计意图 拓展教学内容，让学生自主体验一个完整的建模过程，此为深化与巩固学生理解建模流程的过程，也是增进数学知识与生活实际联系的过程. 学生在建模中体验、思考与感悟，获得“四基”与“四能”的同时，发展良好的数学建模素养.

5. 应用模型，凝练提升

问题1 如果平均每位游客出游一次可给当地带来1000元门票之外的收入，A地景区的门票价格为150元，B地景区没有门票，那么A，B两地景区在2005年至2019年之间，由游客带来的收入有多少？

问题2 某种生物死亡1万年后，其体内碳14的含量会衰减为原来的百分之几？

设计意图 知识到生活的关键在于灵活应用所学知识解决实际问题. 本节课的教学重点是引导学生感知建模过程，发展学生的建模素养，能让学生应用所构建的模型解决实际问题. 引导学生应用指数函数模型来分析上述两个问题，一方面可进一步深化学生对指数函数概念的理解，另一方面可增强学生的知识应用能力，发展学生的数学学科核心素养.

6. 回顾总结，发展学力

课堂尾声，要求学生自主总结建模基本步骤，感受建模思想. 鼓励学生自评、互评课堂中的表现，提升反思与总结能力.

设计意图 回顾学习过程，促使学生自我反省，为构建完整的知识结构奠定基础，也让学生将所学知识与技能转化为内在素养和能力.

教学思考

结合本节课教学来看，数学建模离不开生活实际的支撑，遵循“生活—知识—生活”的流程. 在教学实践中，教师要充分了解学情，以学生认知范围内的实际问题为教学起点，通过问题驱动建模教学，并将提问的权利还给学生，从真正意义上激发学生的潜能，发展学生的数学思维和数学学科核心素养.

值得注意的是，从知识到生活的高中数学建模实践在发现并提出问题、建立模型、求解模型与完善模型等环节，一定要基于深度学习的角度出发，时刻遵循“以生为本”教学理念，避免流于形式，此为发展学生数学学科核心素养的重要举措.

总之，数学建模源于生活，服务于生活，其内容和理念应根植于生活之中［2］. 建立在学生已有认知基础上，根据学生的生活经验构建数学模型，不仅能体现生活的“数学味”，还能凸显数学知识的“生活味”，揭露知识与生活的关联性. 从知识到生活的建模实践，需教师反复探索与打磨，设计出科学的情境问题，提升学生的创新意识，发展学生的建模素养.

参考文献：

［1］ 周学君，龚雨欣，董清艳. 指向数学建模素养的高中数学教学设计框架及实施：以人教A版“指数函数的概念”为例［J］. 黄冈师范学院学报，2023（12）：80-85.

［2］ 周颖. 从知识到生活的高中数学建模实践研究［J］. 数学教学通讯，2023（18）：52-53+60.