多元表征的理论基础与应用措施的研究

［摘  要］ 将单一的问题用多种形式表示，可增加学生表征的视角，提高学生的表征能力. 文章从多元表征的理论基础出发，以“平面向量基本定理”的教学为例，具体从以下四方面展开教学与思考：旧知回顾，设置问题；问题驱动，探索新知；多元表征，完善定理；总结归纳，获得图式.

［关键词］ 多元表征；认知负荷；应用措施

作者简介：李明（1979—），本科学历，中学一级教师，从事高中数学教学工作.

多元表征是当前国际数学与教育心理学研究的热点话题. 实践证明，多元表征的应用能深化学生对知识本质的理解，增强知识的正迁移，促进学生思维与能力的发展. 多元表征主张通过对问题模式与规则的观察，将一般问题转化为具体问题，并应用多种观点表达同一问题，达到顺利解题的目的.

■ 理论基础

1. 认知模型理论

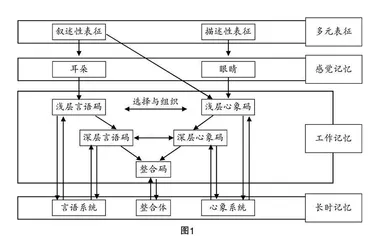
从信息加工角度来看，数学多元表征是指人脑对表征信息进行提取、加工与贮存的过程，有工作记忆与长时记忆两个系统（见图1）. 认知模型理论从认知角度出发，对数学信息进行辨认，一般遵循以下步骤：第一步，信息直接作用到学生的感官，学生初步形成第一阶段感知，获得“感觉记忆”，这种记忆模式储存时间短，往往几秒钟以后就会遗忘；第二步，教师进行适当引导，让学生形成第二阶段的“组织记忆”，信息经过组织形成浅层心象码与浅层语言码；第三步，深化学生对信息的理解，促进深层心象码与深层言语码的形成；第四步，变换与转译表征间的编码，形成整合码，获得工作记忆，而后经过存储形成长时记忆.

2. 双重编码理论

加拿大学者Paivio等人于1970年提出双重编码理论，对教育产生了重要影响. 该理论认为，图象记忆强于文字记忆，若在同一时间呈现同一件事物的言语与非言语信息，和仅呈现一种信息相比较，前者更利于学习者形成言语码与心象码.

双重编码理论对多元表征具有重要的促进意义，该理论的实证研究给多元表征指导下的教学策略提供了重要方向. 比如我们所熟悉的几何直观化、代数化过程等，都可以将文字或语言转化为直观可视的图象，这对学生的学习起辅助作用.

3. 认知负荷理论

20世纪80年代，澳大利亚学者Sweller等人共同提出认知负荷理论，该理论对教育学和心理学领域产生了重要影响. 该理论认为，认知负荷分为内在、外在与有效三种类型.

在认知负荷的启发下，基于多元表征视角进行教学设计，需要考虑到知识的信息结构，同时还要注意策略的呈现以及无关信息的剔除等，要保证有效认知负荷的产生. 因此，基于多元表征理念的教学设计要着重关注认知负荷情况，尽可能让认知负荷一直处于工作记忆状态.

■ 教学分析

平面向量基本定理是向量知识模块中的重点内容，学生在应用这部分知识解决实际问题时，常出现如下几种障碍：①从向量本身来看，它存在大小与方向两种属性，类比物理知识容易理解，但难以掌握该定理所蕴含的数学思想方法，应用时错误百出；②对这部分知识的认识处于静态，难以进行知识的整合与建构，更谈不上应用.

将多元表征理念应用在平面向量基本定理的教学中，能让学生自主发现问题，体会特殊和一般之间的灵活转化与化归，感知数形结合思想等，实现知识的整合与建构.

■ 教学过程简录

1. 旧知回顾，设置问题

首先要求学生回顾与平面向量相关的知识，说说当时的学习方法. 在笔者的启发下，学生表示学过向量的加减法、数乘、向量共线定理等知识，并大致描述了当时的研究方法.

师：之前我们通过向量的数乘获得了向量的共线定理，明确了一个向量可以表示另一个向量，且两者可以互相表示. 本节课我们就研究平面内任一向量是否可以由同一平面内的两个不共线向量表示.

设计意图 旧知的回顾起到唤醒的作用，让学生通过有效信息的提取，进行有意义的思考. 笔者从共线向量的关系出发，揭示本节课的探究主题——平面内任一向量可以由同一平面内的两个不共线向量表示. 这种方法能快速吸引学生的注意力，让学生自然而然地进入新知的探索.

4. 总结归纳，获得图式

本节课的课堂小结，笔者引导学生以图示的方式进行高度概括、深化整合. 经归纳与总结，学生将本节课的关键内容整理如下：

一个定理：平面向量基本定理；

三个特征：任意性、不共线、唯一性；

两个数学思想：数学方程思想、数学转化思想.

设计意图 对一节课的回顾与总结，是学生自主理清知识脉络、提炼数学思想方法的过程，也是完善认知结构，获得概念内部心象码、生成整合码的过程. 因此这个环节起着重要的承上启下作用，是后续学习的关键.

■ 教学策略思考

1. 信息注意策略

对于平面向量基本定理而言，这是一个复杂且抽象的定理，单一的表达方式不足以引起学生的深度理解. 而多种表示形式的呈现，可引发学生对定理本质的认识. 因此，教师可在教学过程中引导学生对关键信息进行提炼、标注，让学生将更多的精力投入到有意义的信息中来. 如定理讲授时，教师先借助PPT展示定理，并要求学生根据文字描述将定理的关键性质罗列出来，这属于信息注意策略的应用.

2. 多元表征策略

在信息打包原则下进行平面向量基本定理的教学，应引导学生从多元表征的角度对定理进行描述，以促进学生对定理非本质属性的认识. 平面向量基本定理是一个抽象的定理，若仅用一种表征形式根本就无法揭露其本质. 鉴于该阶段学生的抽象水平有限，教师在教学时应尽可能向学生呈现多种表征形式，以增强学生的理解程度.

3. 变式教学策略

变式是基于知识本质的训练方式，与多元表征的本质具有统一性. 本节课的变式应用，不仅让学生多维度了解了表征对象，还让学生更好地应用所学知识解决了问题. 这种教学策略，一方面让学生对教学内容的各种形式有了进一步的认识，另一方面让学生对知识间的联系有了研究. 因此，变式应用可以让学生更深层次地认识平面向量基本定理.

总之，多元表征能帮助学生建构良好的认知结构，激发学生生成整合码，让学生对学习内容形成长时记忆，利于后期学习应用. 因此，这是一种值得推广的教学模式，需要教师用清晰的思路，站到宏观的角度设计教学，为提升学生的数学学科核心素养奠定基础.